用微元法轻松推出弧长公式
【告别记公式】用微元法轻松推出弧长公式_哔哩哔哩_bilibili
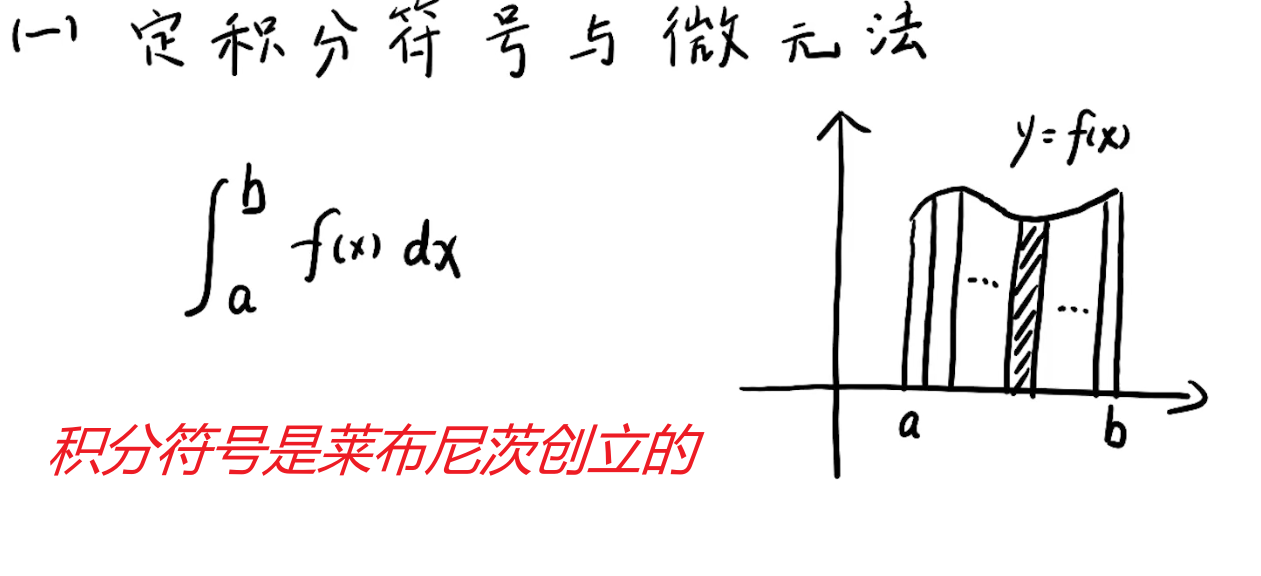
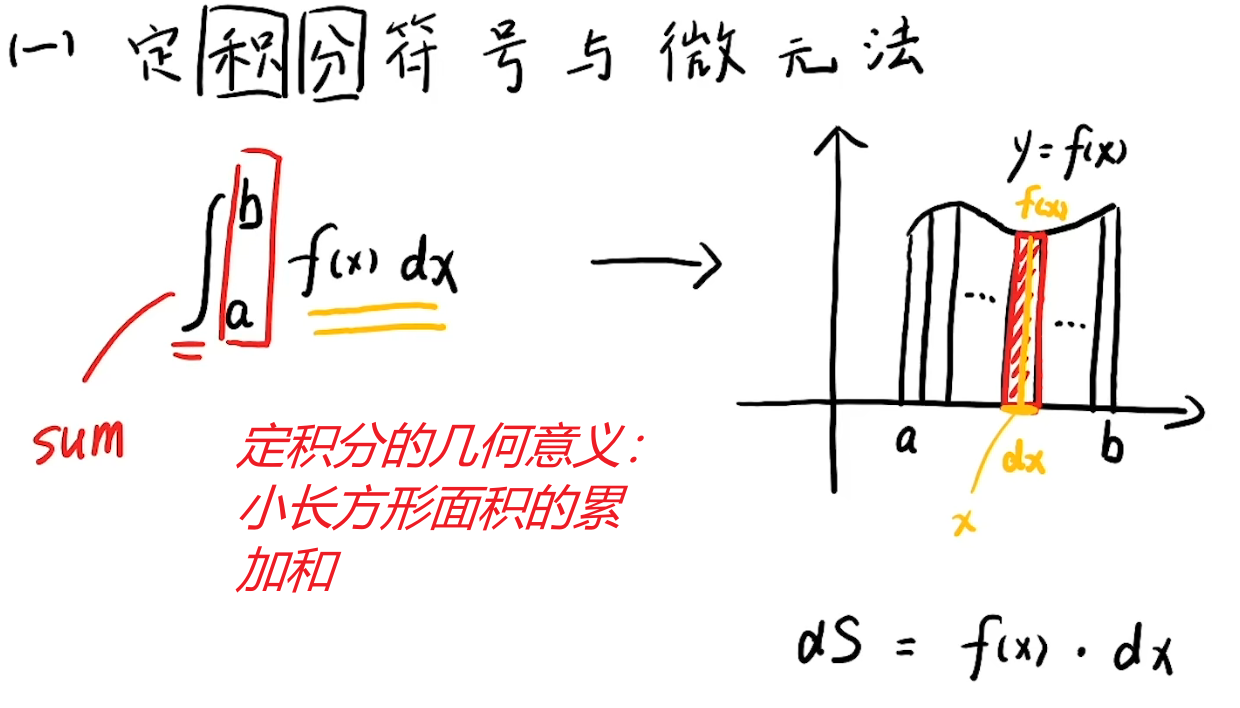
注解:
1.
分:小部分
积:累加
积分就是把小部分给累加起来。
2.定积分:计算曲边梯形的面积
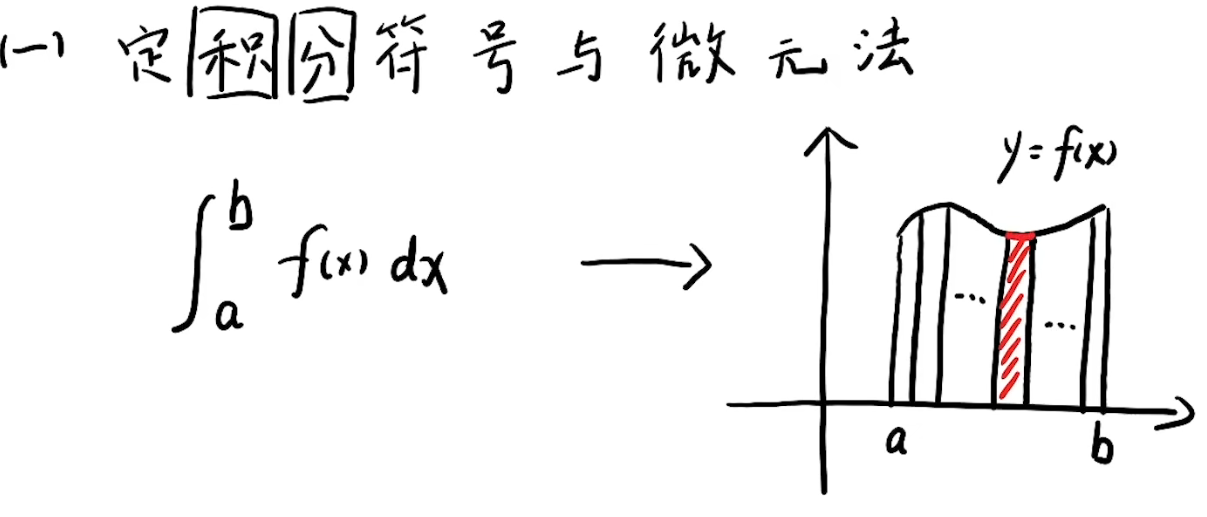
注解:
1.在小梯形分的特别细的时候,小梯形上边的曲线就可以近似看成是平的,也就是看成是直线了。小微元可以近似看成是小矩形,这时候的误差是很小的。
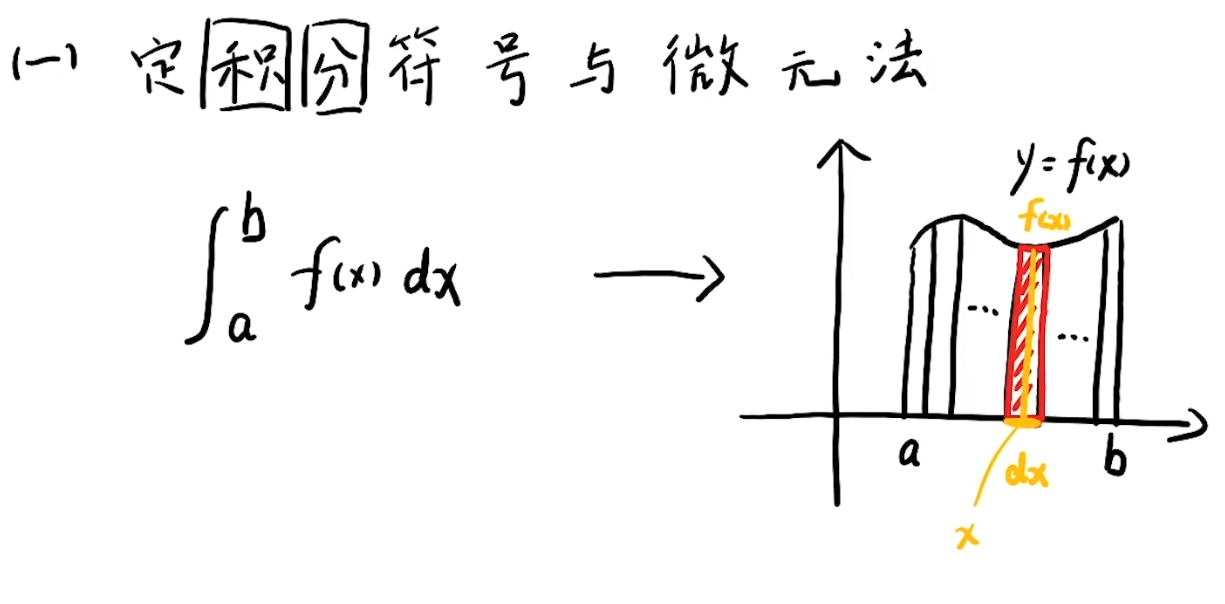
注解:
1.dx是微分的概念,就是一小段x,当dx很小很小的时候,就几乎变成了(等同于)一个点了,这个点设为变量x。
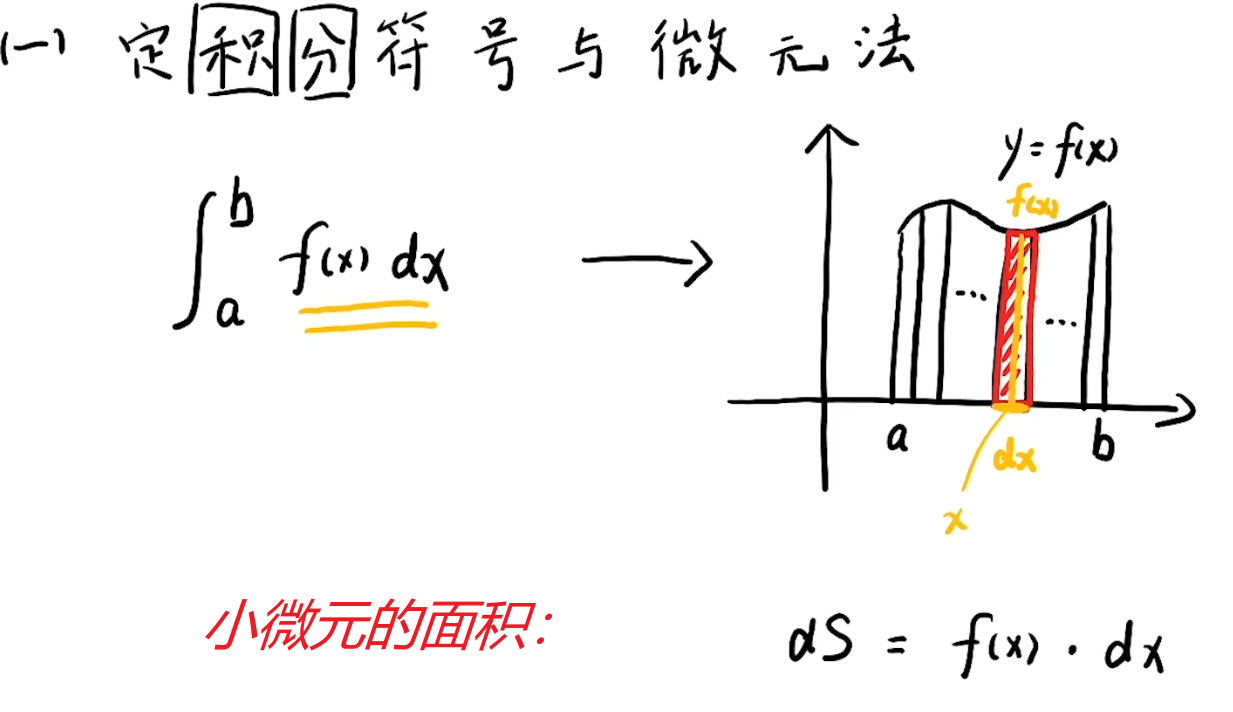

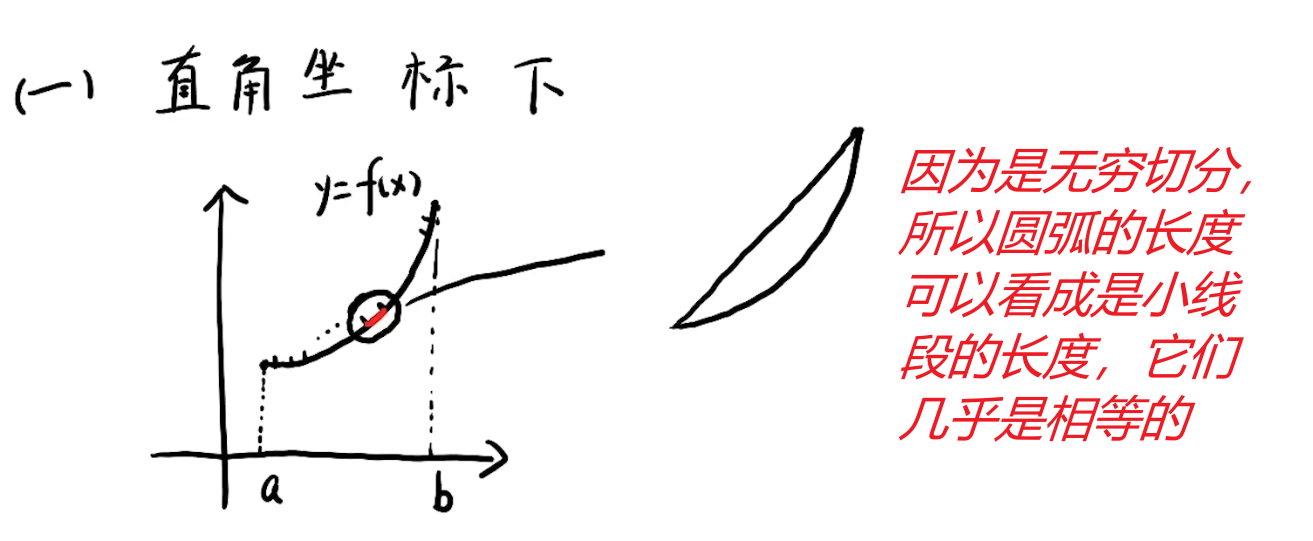
注解:
1.整体思想是:求出一个小弧长(微元)的长度,然会累加到一起。
2.小线段即是小弦长,求出这个小弦长的长度即相当于是求出了小弧长的长度。
3.那小微元的长度有多长呢?下面进行放大处理并求取。
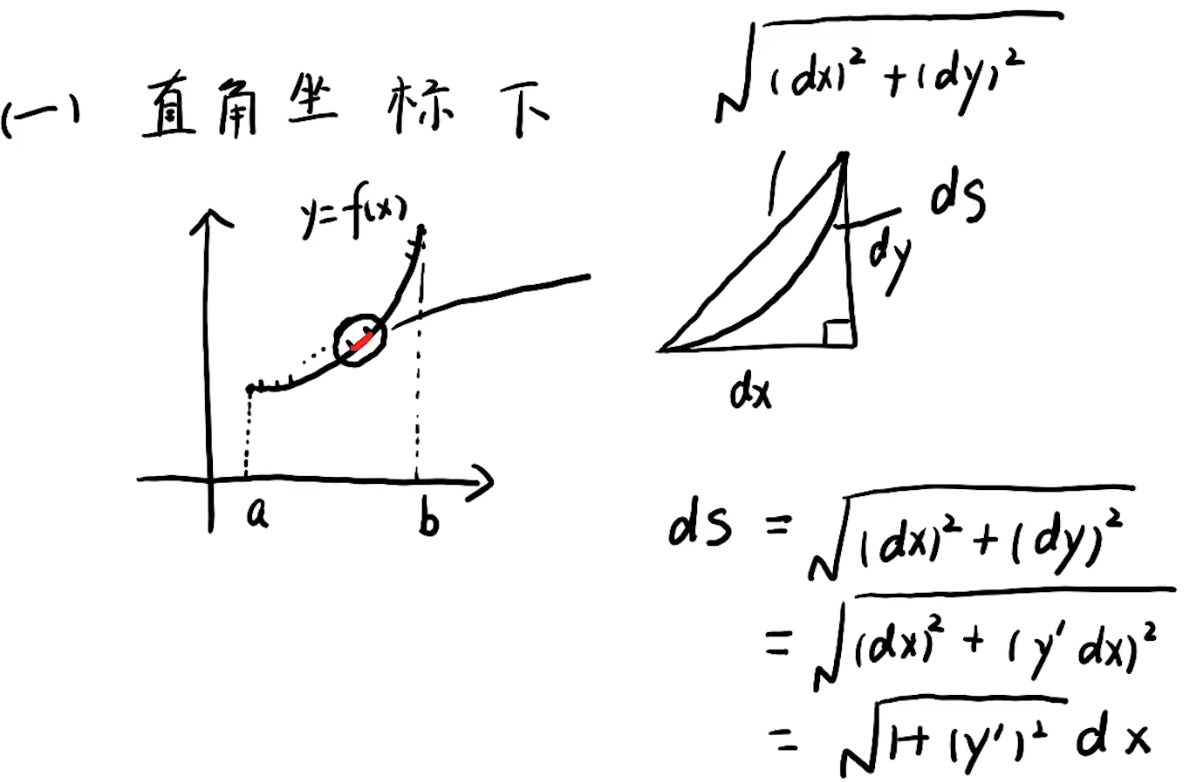
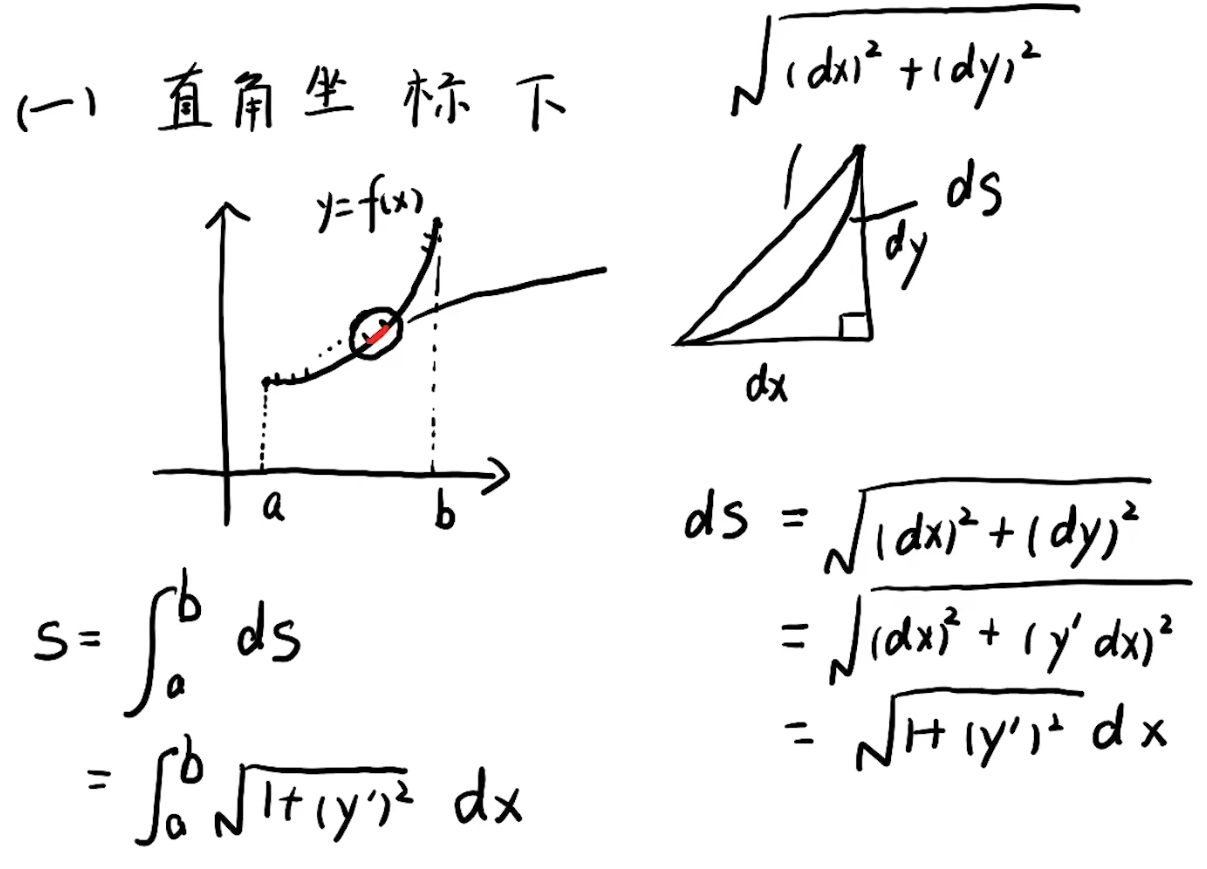
注解:
1.s的表达式就是弧长公式。
网友讨论:
![]() ?
?

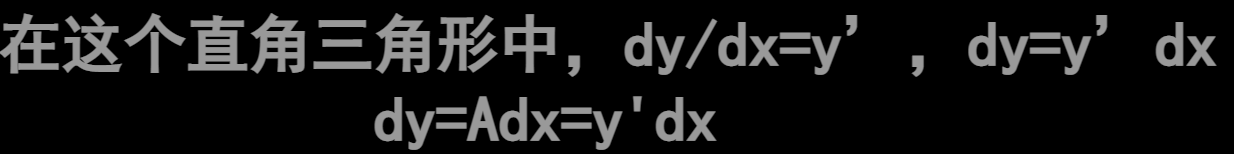
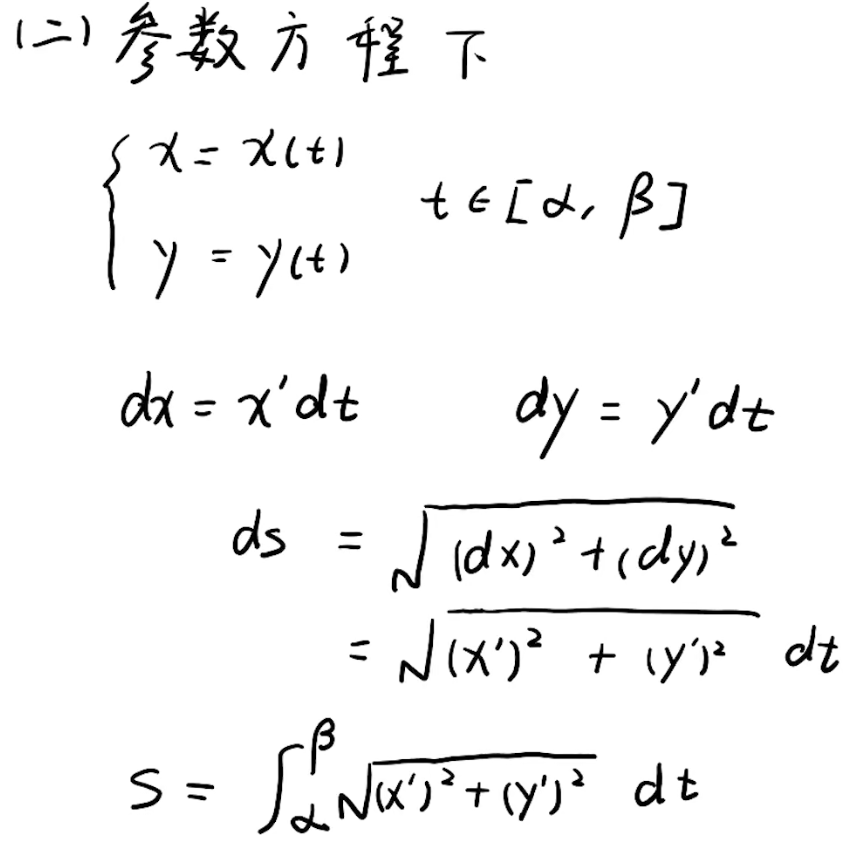



 浙公网安备 33010602011771号
浙公网安备 33010602011771号