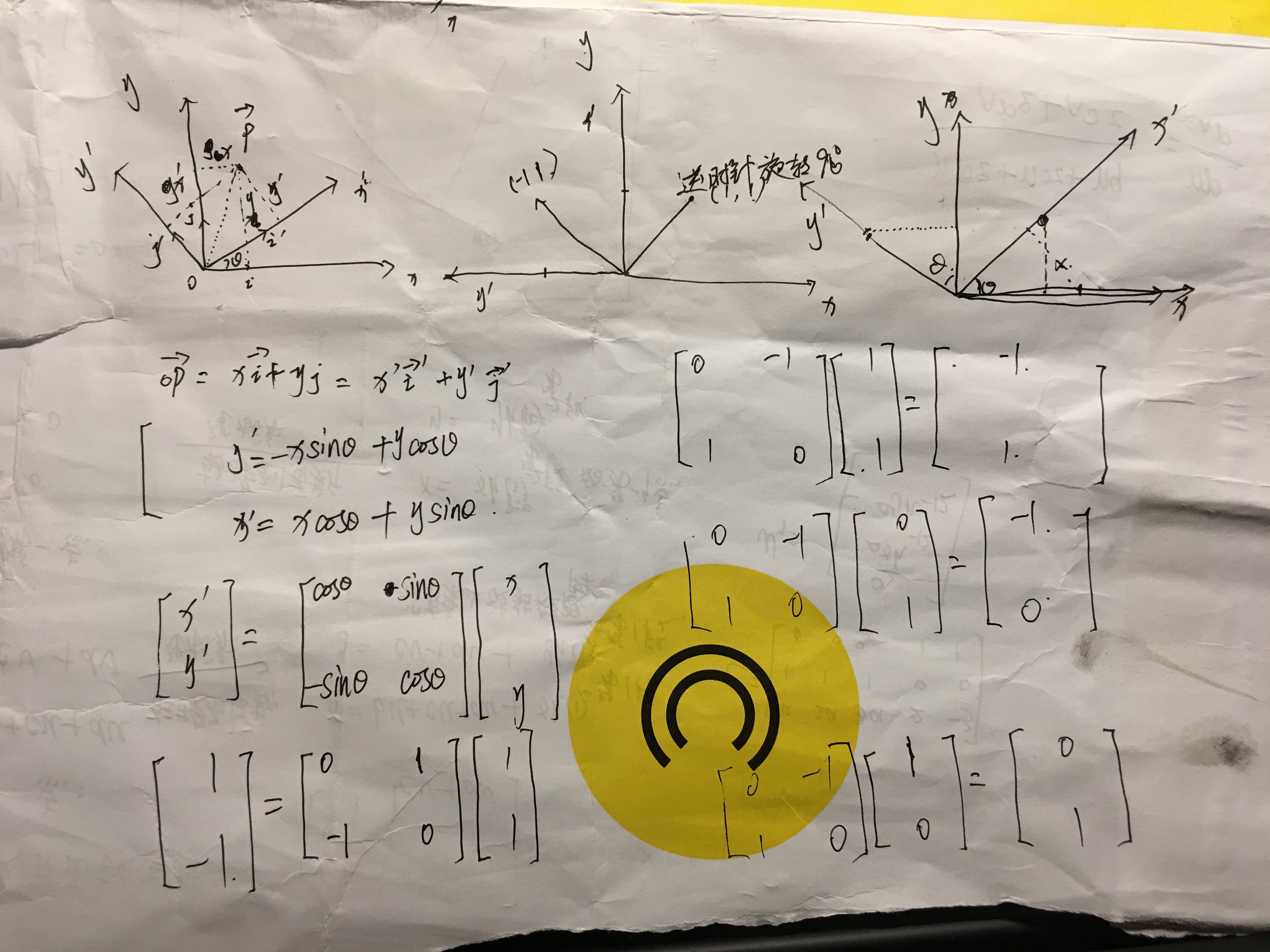
旋转矩阵、坐标转换和向量的旋转

1.坐标转换

 

 

注解：

1.三维的坐标转换的推导和二维的是类似的。

2.规律是：右手坐标系的情况下，绕Z轴逆时针旋转的话，负号写在旋转矩阵的左下角，顺时针旋转的话，负号写在旋转矩阵的右上角。如果是左手坐标系，则正负号的规律要反过来。

3.在三维空间中，2的规律适合右手坐标系，假如坐标系是左手系，则可以先把坐标系转变为右手坐标系，再做坐标的旋转。也可以这样记：右手系的正负号规律和左手系的正负号规律是相反的。

关于坐标旋转和平移的顺序，思考1:

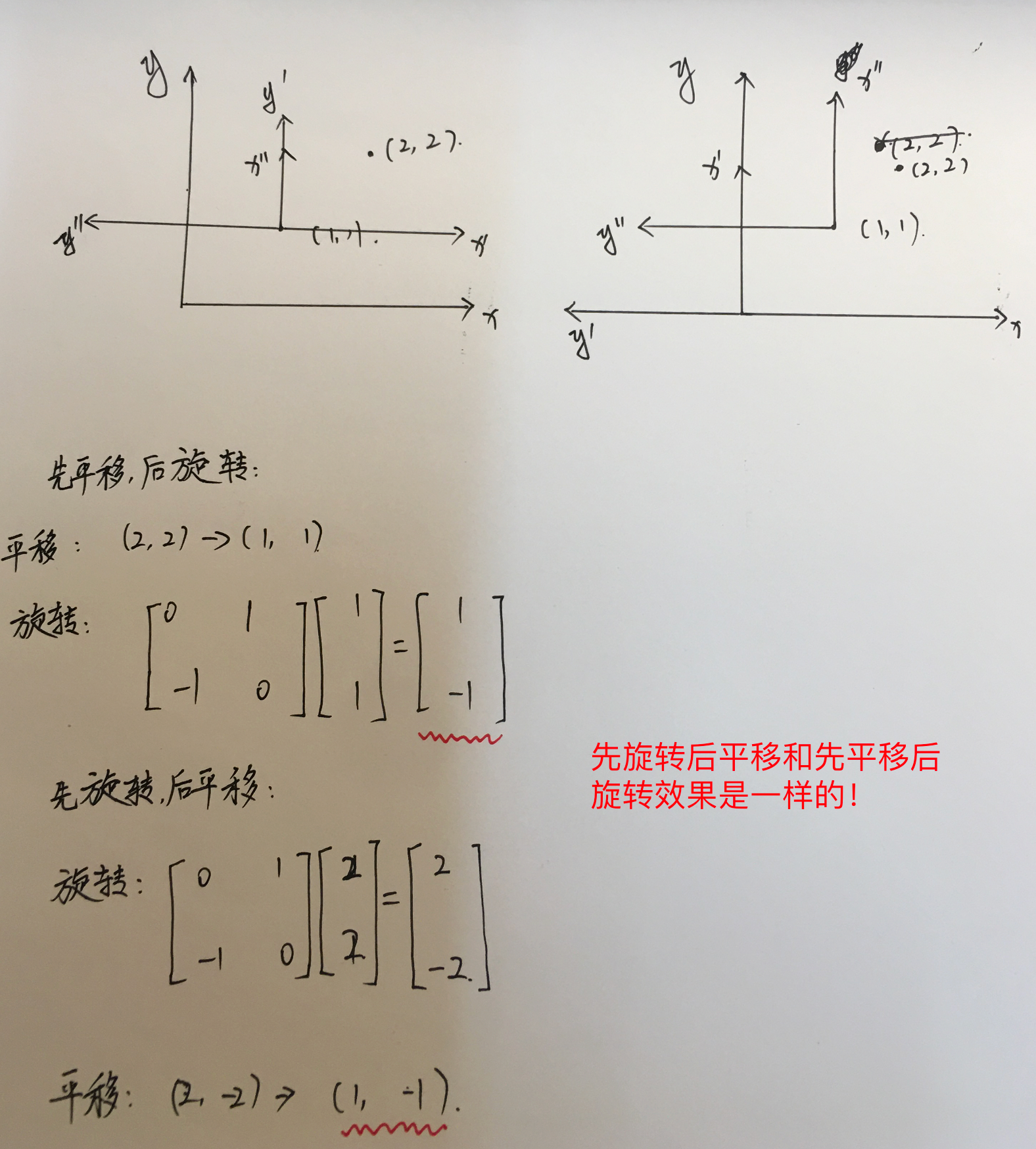
思考2:

 

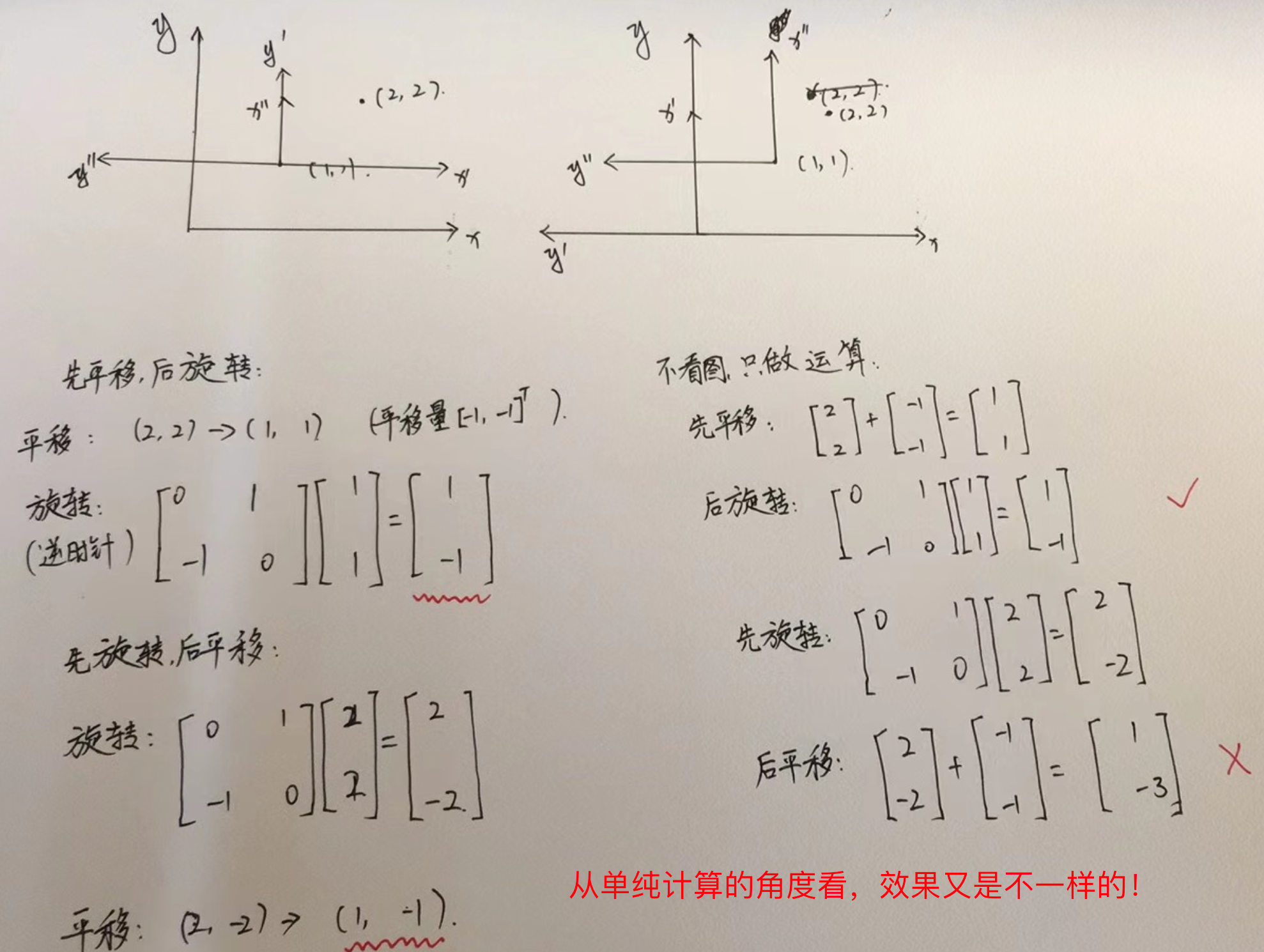
小结：

坐标系的平移和旋转，顺序不一样， 效果不一样。

思考3:

 

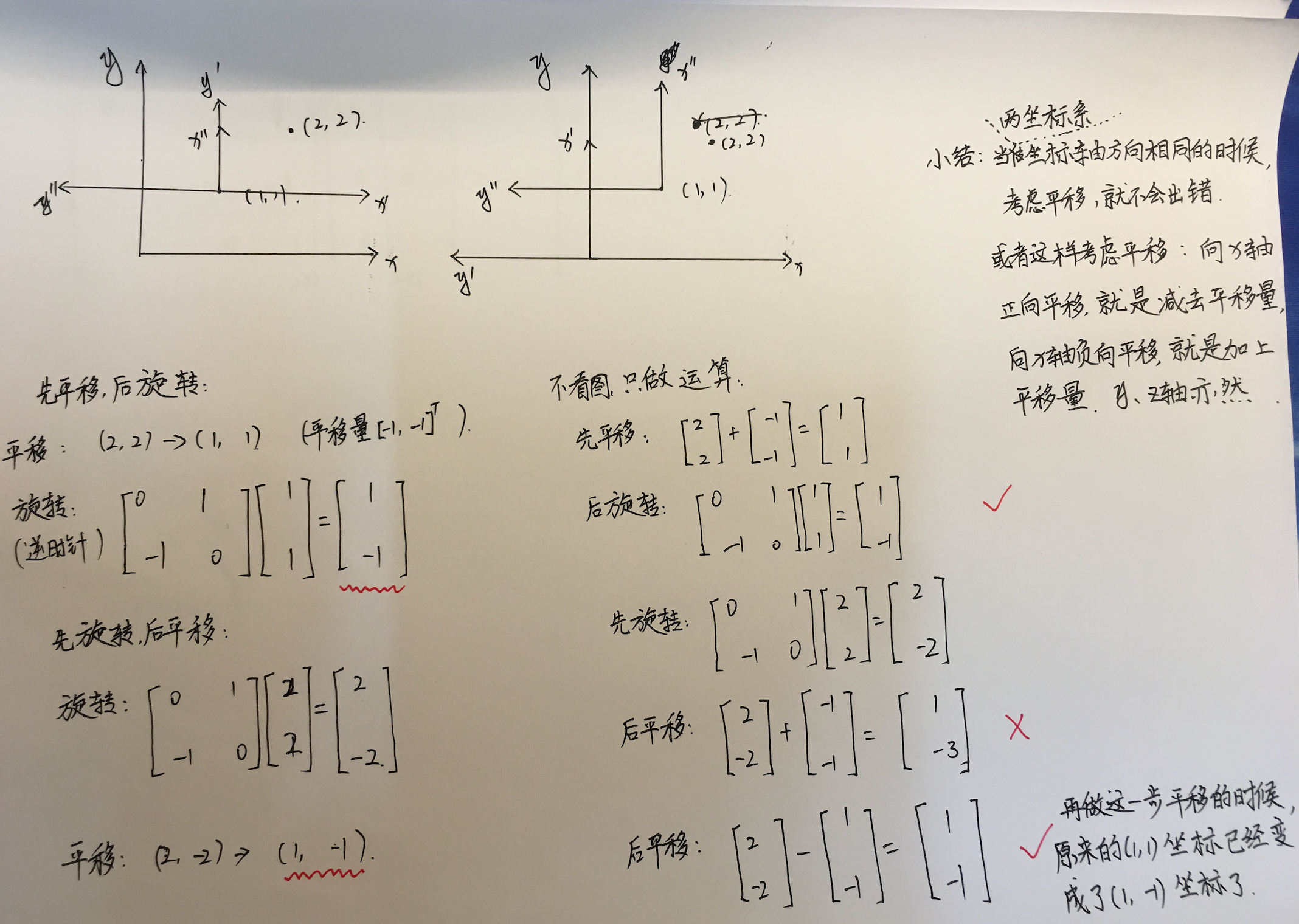
把旋转和平移统一起来：

 

 

 

 

 

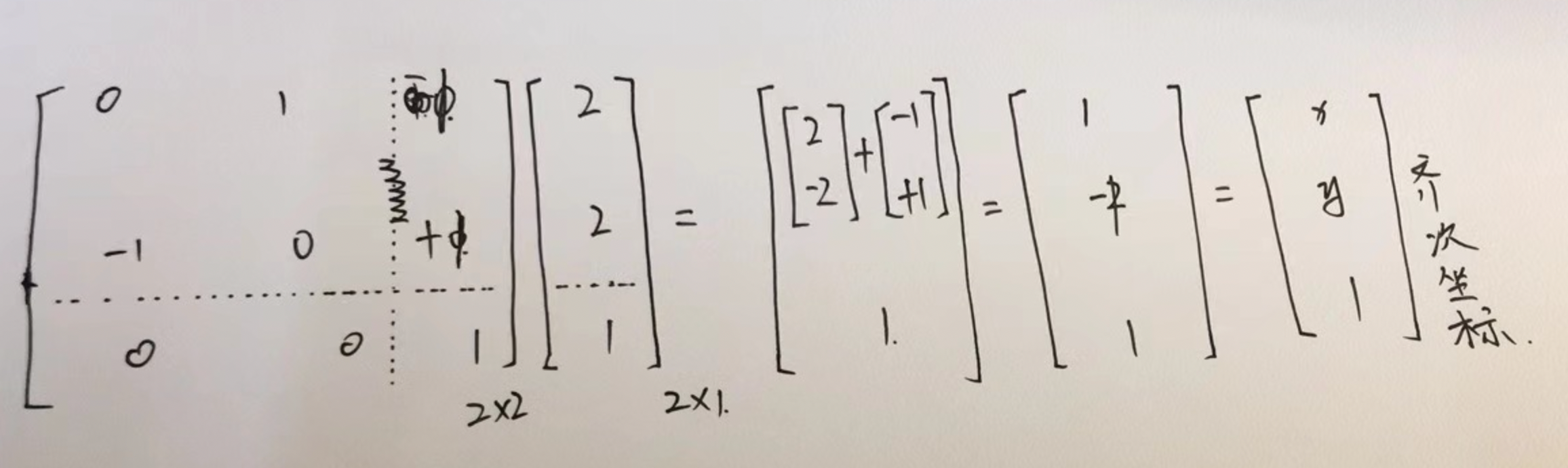
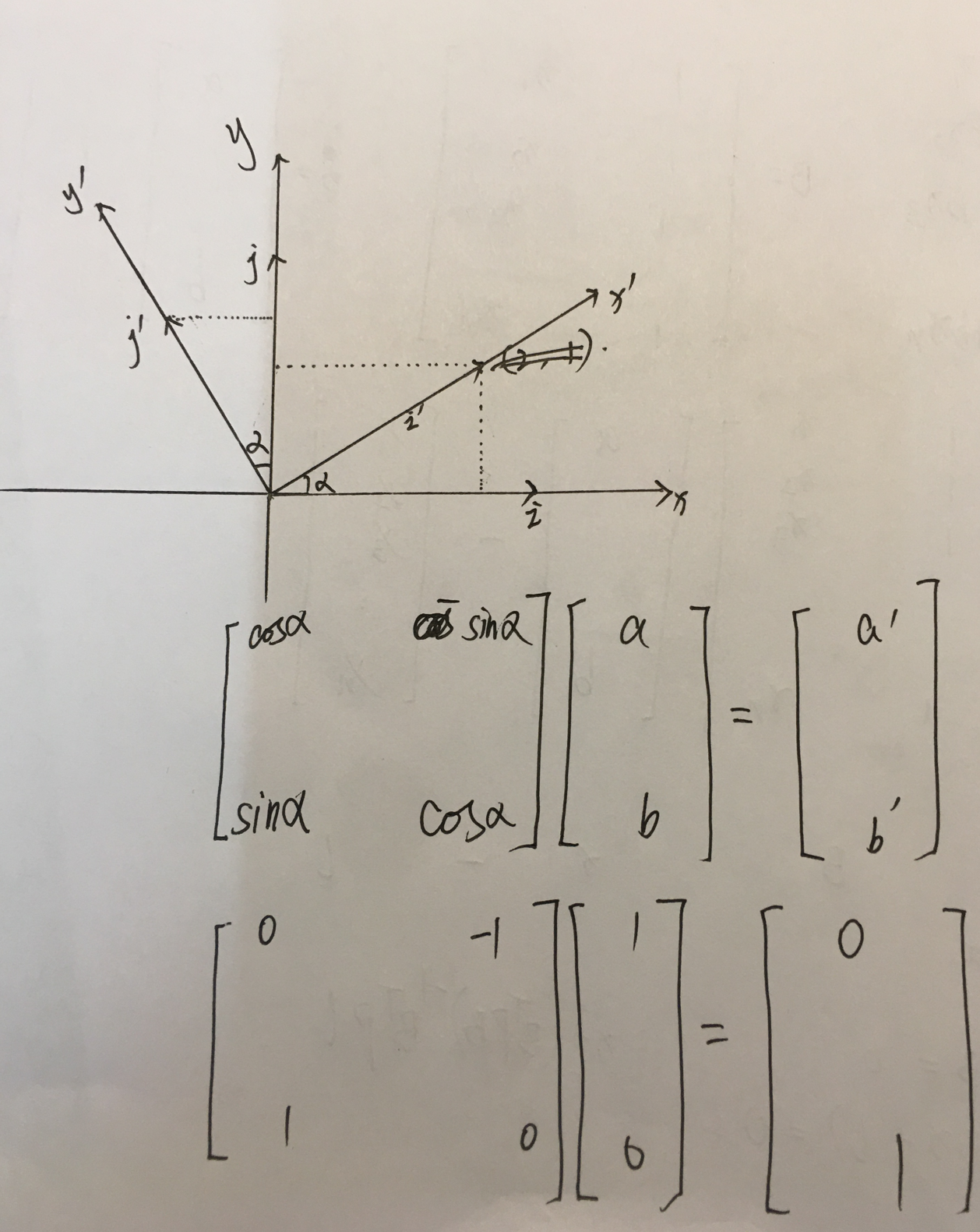
2.向量旋转

向量的旋转和坐标转换不一样。

 

任意一个向量左乘上一个上图的旋转矩阵，相当于把向量逆时针旋转α°。此时向量旋转前后的坐标都是在原始坐标系x-y坐标系中的坐标。例如，当α=90°的时候，第二个旋转矩阵乘上向量：

会把这个向量旋转90°，变成：

。

 旋转矩阵的对角线上的元素和向量或图像的的缩放有关，即限制着向量或图像的的缩放，副对角线元素对和向量或图像的旋转有关，即限制着向量或图像的的旋转。

 也可以这样考虑：这个旋转矩阵相当于是让原来的坐标系顺时针旋转90度，那么[1 0]^T向量在新坐标系中的坐标是0 1]^T

 

注解：

1.第一列元素的平方和应该等于1.

2.第一行的元素的平方和应该也等于1.