矩阵和变换
一个矩阵就相当于一个基。
例如:
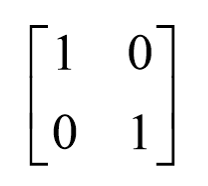
这个矩阵是我们常见的基,是笛卡尔坐标系的基。
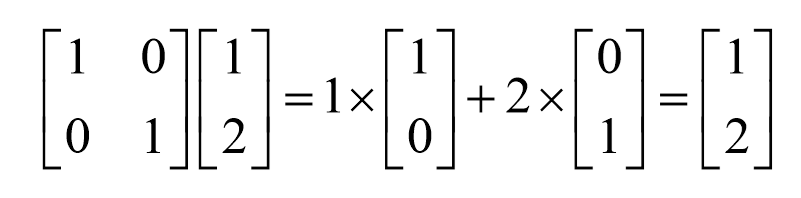
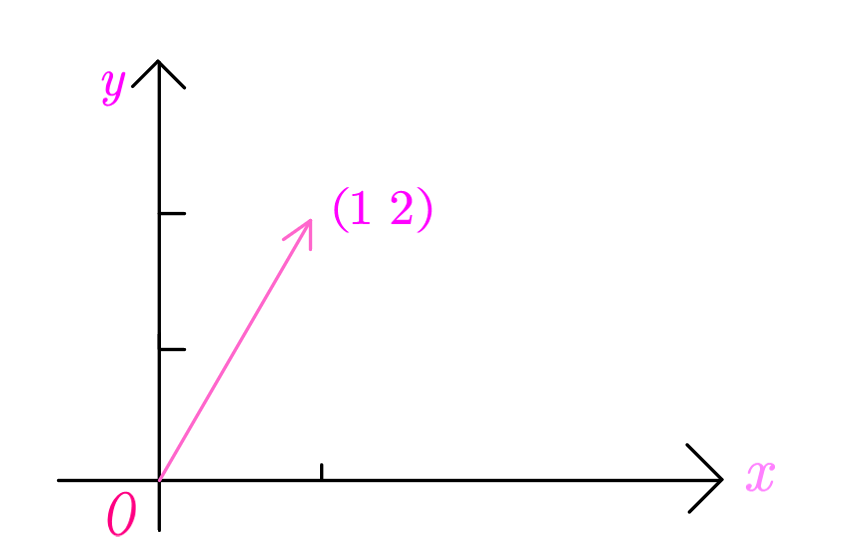
在这个基的作用下,向量被映射后,还是它本身。相当于是1倍的![]() 向量加上2倍的
向量加上2倍的![]() 向量。
向量。
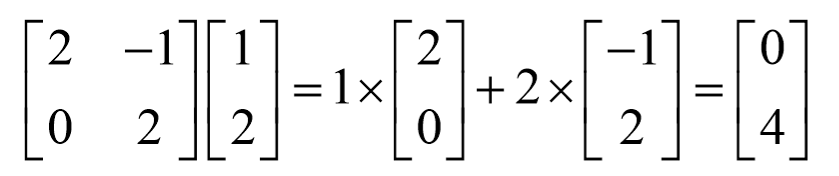
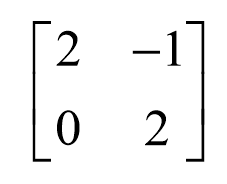 这也是一个基。
这也是一个基。
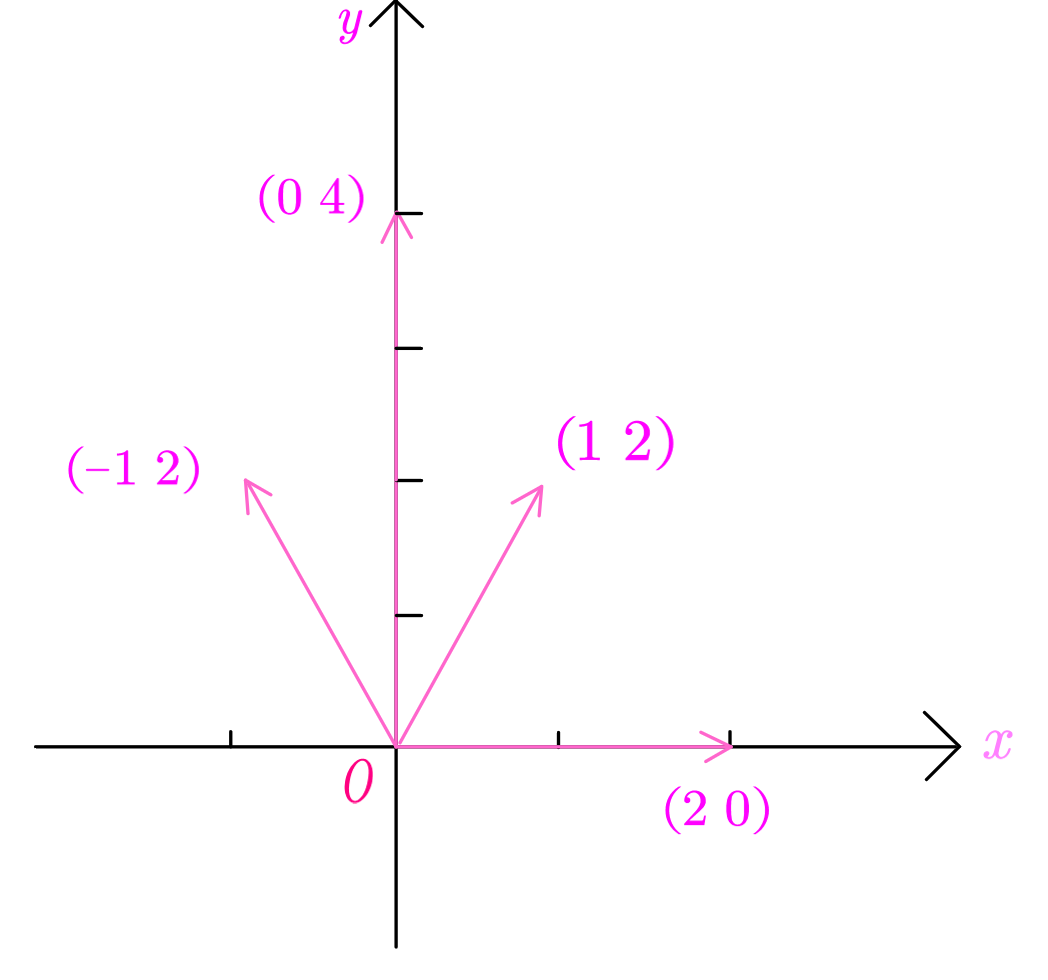
在这个基的作用(映射)下,向量![]() 被映射成了
被映射成了![]() ,这个结果仍然是相当于1倍的第一个基+2倍的第二个基的结果。
,这个结果仍然是相当于1倍的第一个基+2倍的第二个基的结果。
一步一步的来:
第1步:首先把第1个基变成:
![]()
即把![]() 在x轴方向上伸长为原来的2倍。
在x轴方向上伸长为原来的2倍。
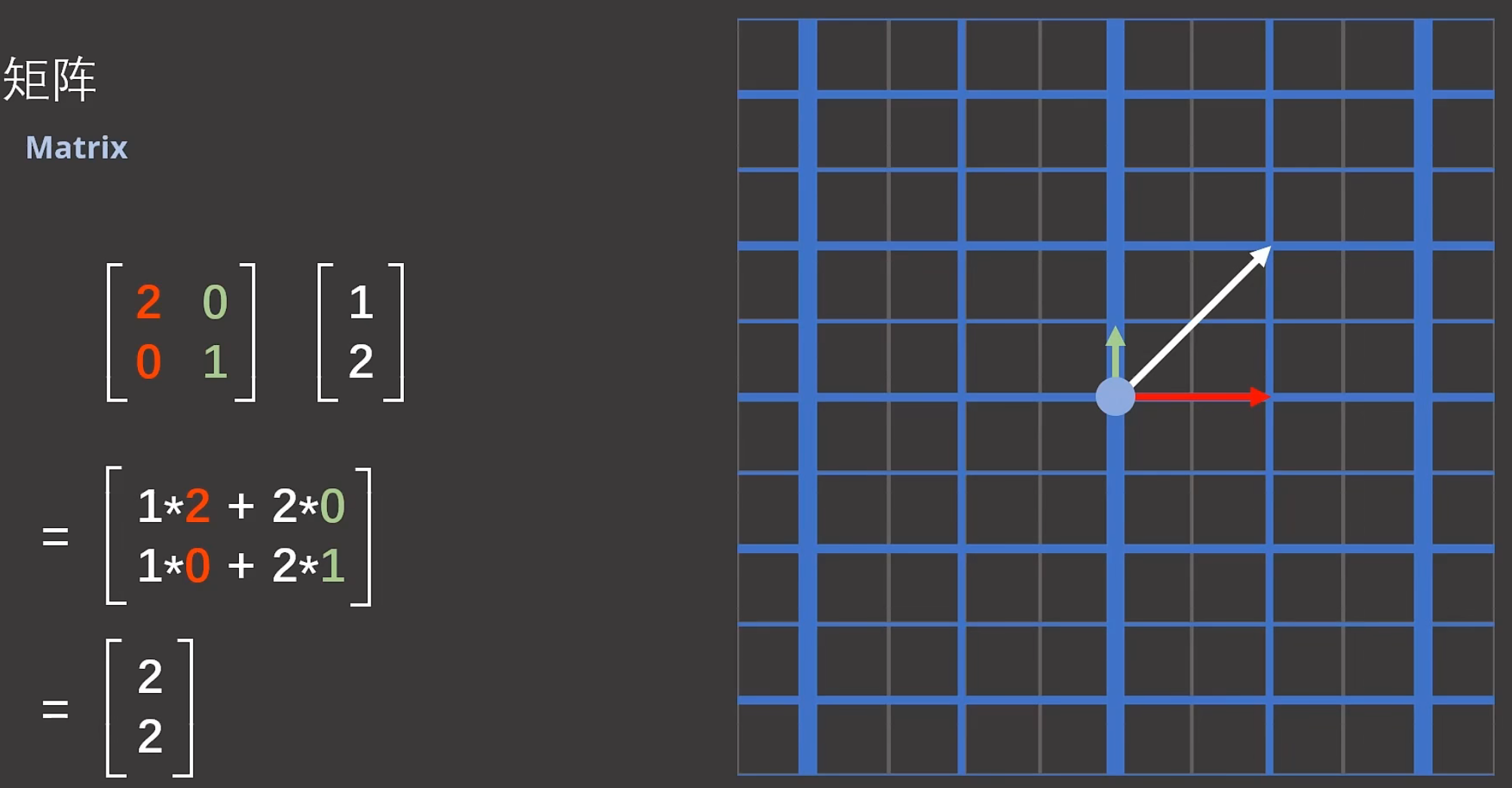
第2步:把第2个基变成:
![]()
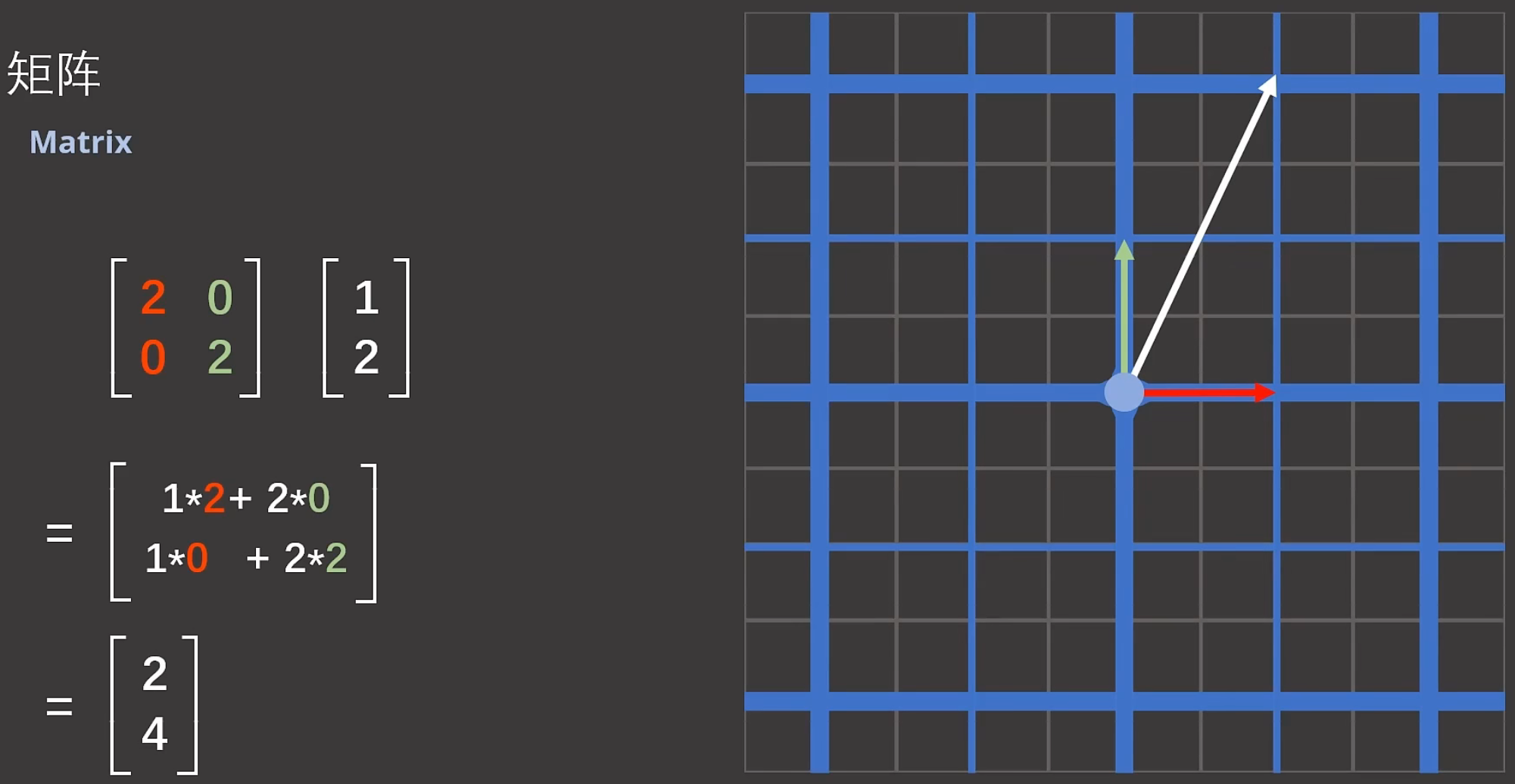
第3步:把第2个基变成:
![]()
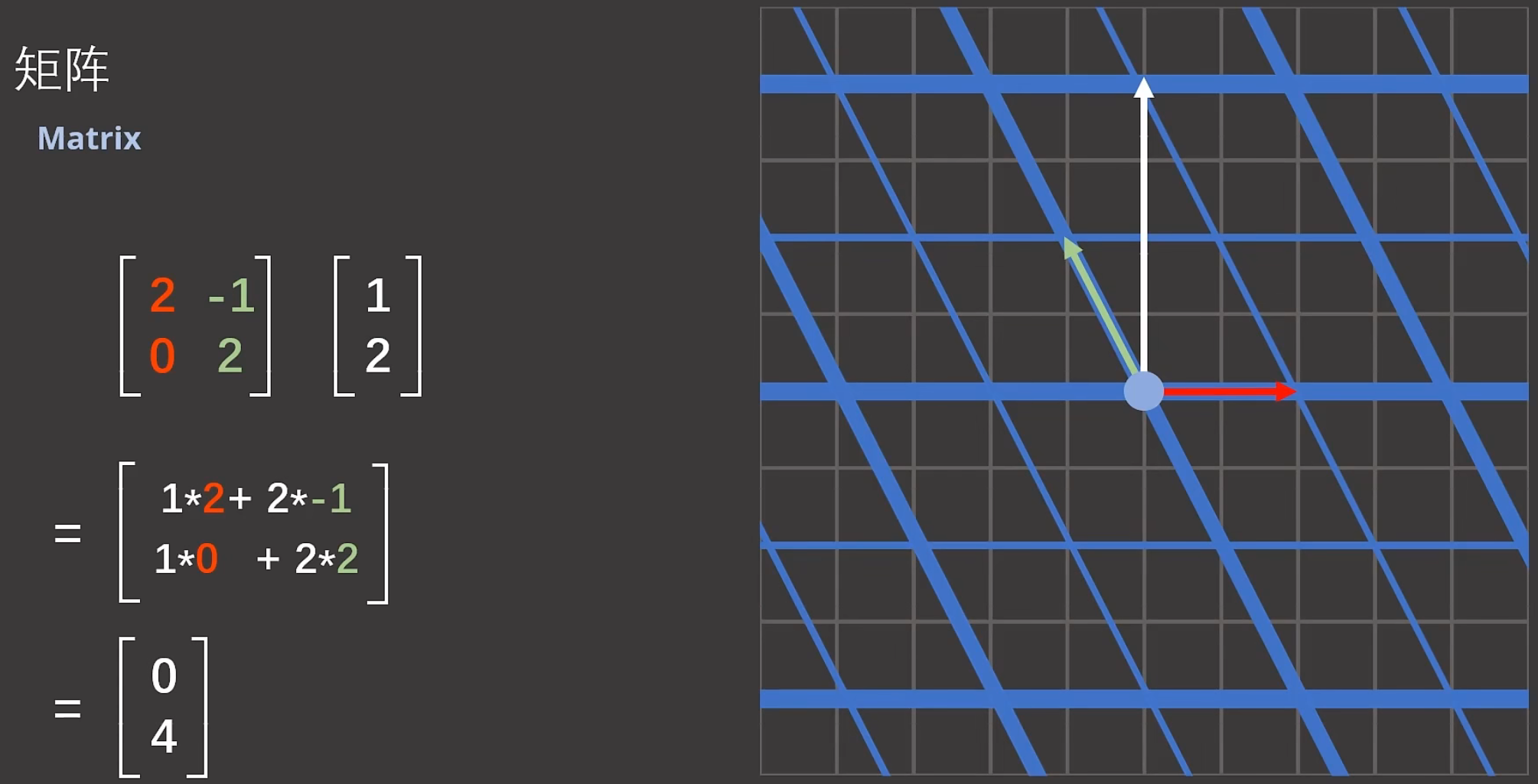
![]()
![]()
白色向量在奇怪的坐标系(新基准构成的坐标系)里面,在横轴上还是一个单位,在纵轴上还是2个单位,相当于在新基准中,还是![]() 向量。只不过回到原始的坐标系中,就是
向量。只不过回到原始的坐标系中,就是![]() 向量.
向量.
![]()
![]()
![]()
如果是行向量和矩阵相乘,那么,矩阵的每个行向量组成新坐标系的基。如下:
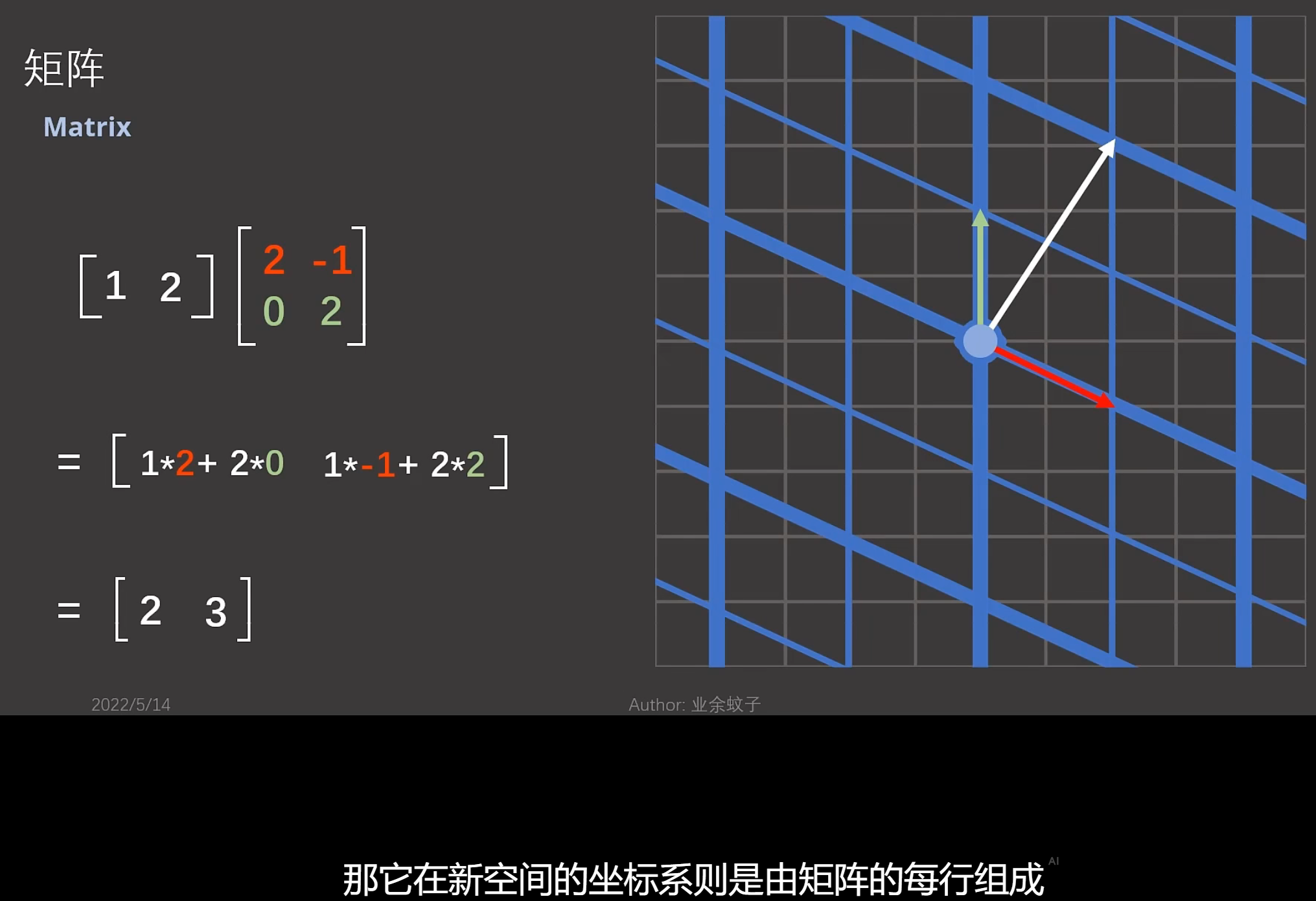
但是,一般是考虑矩阵和列向量相乘。

注解:
1.先向p向量移动x个单位,再向q向量移动y个单位。
2.假如p、q向量分别是标准笛卡尔坐标系中的x轴和y轴,那么结果就是坐标或者向量
![]()
3.p向量和q向量,相当于是标准笛卡尔坐标系中的x轴和y轴。

注解:
1.p向量和q向量,还有另外的名字,叫做基向量。
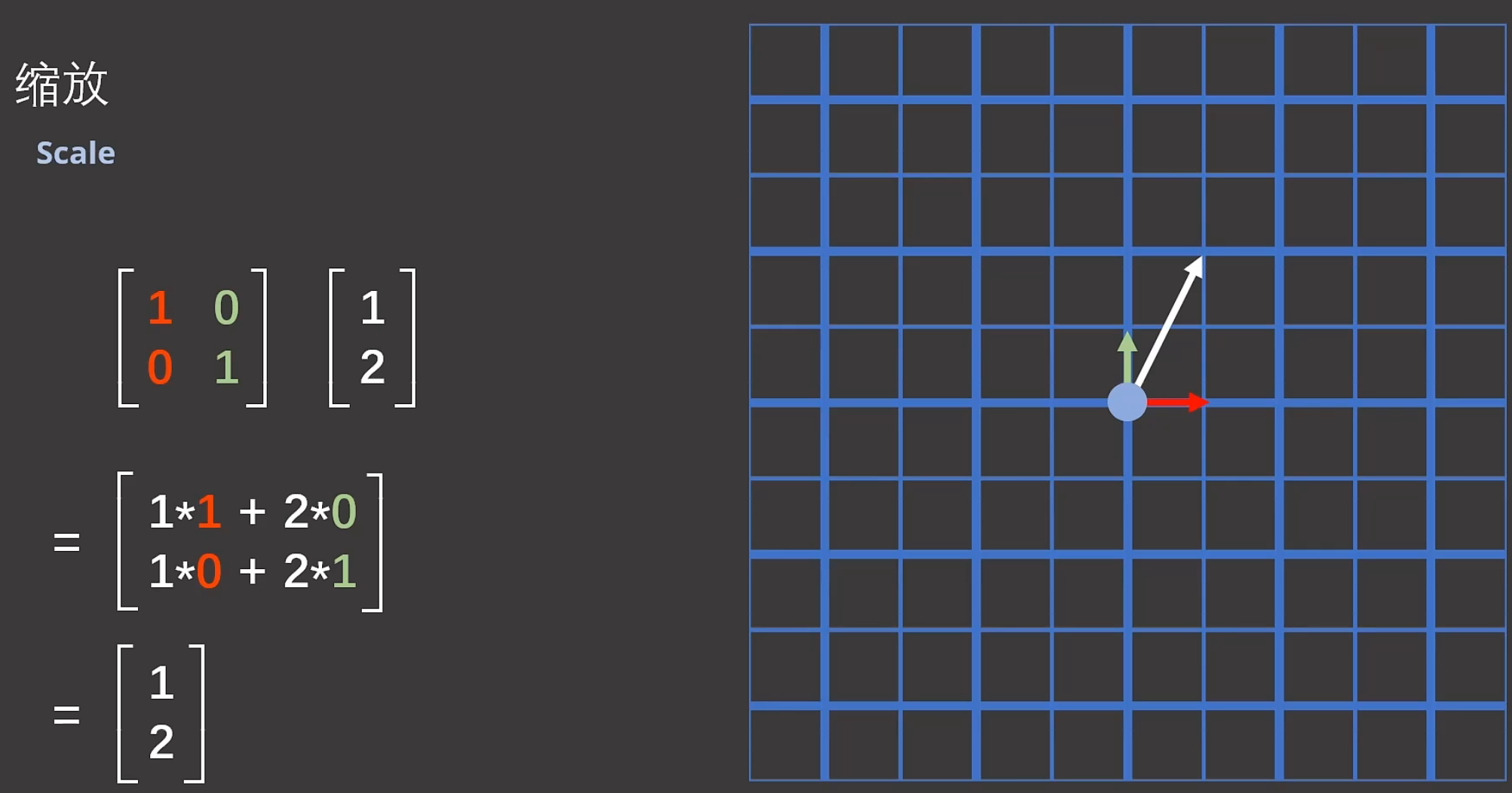
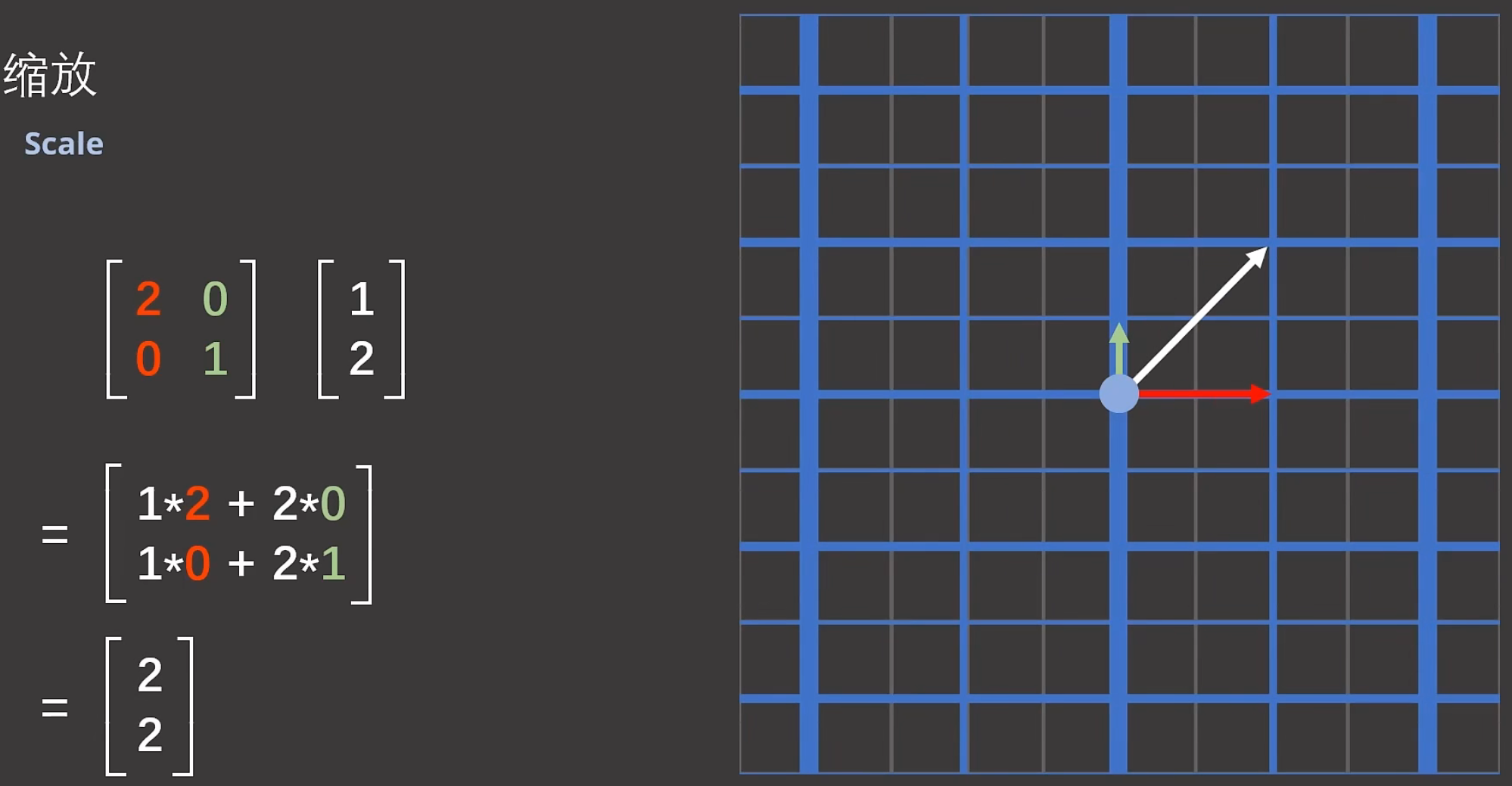
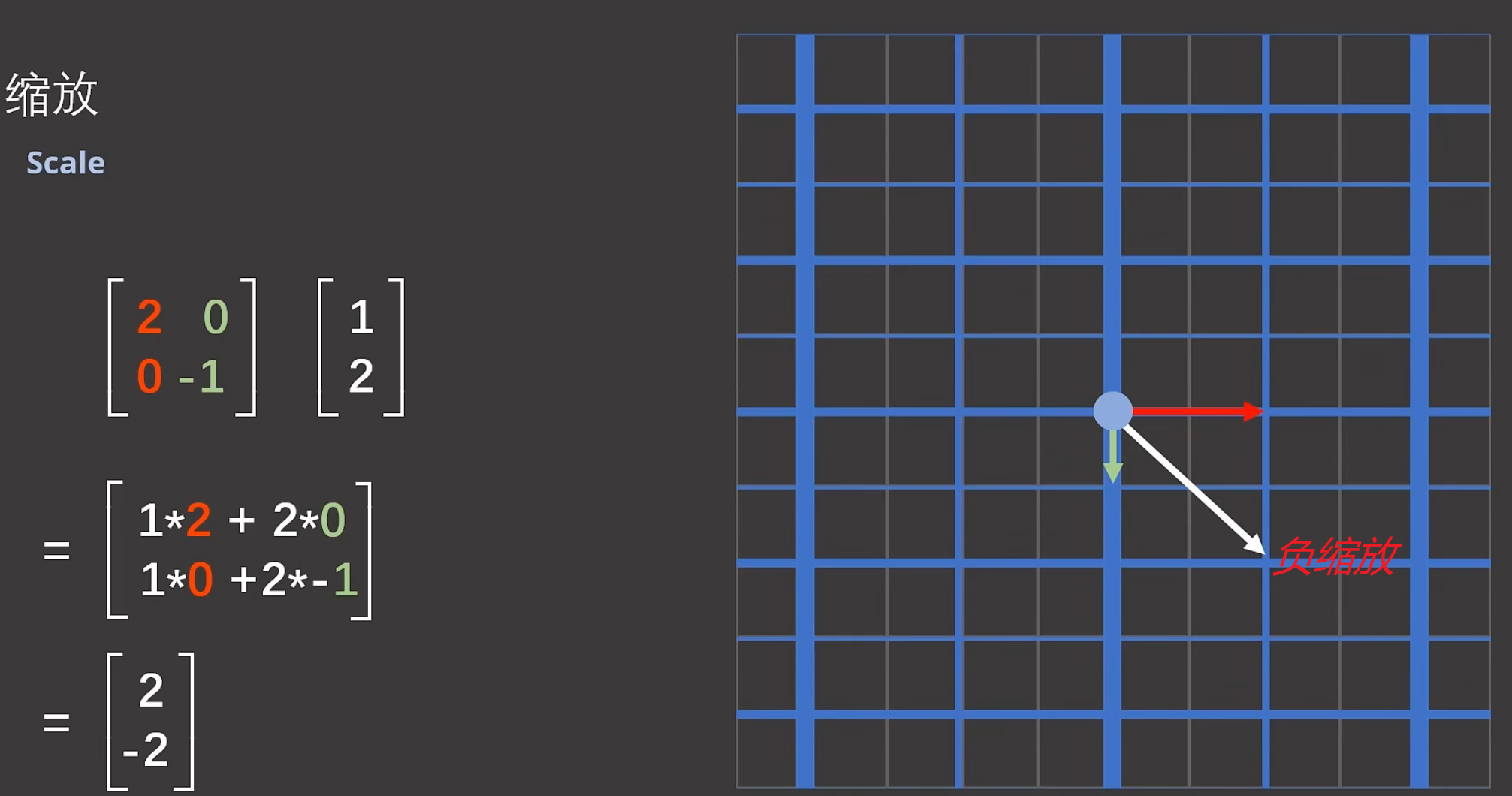
注解:
1.缩放其实最简单,因为只需要修改矩阵对角线上的元素就行了。
2.在同一个坐标系下,矩阵会把向量[1 2]映射到 [2 -2].
旋转:
![]()
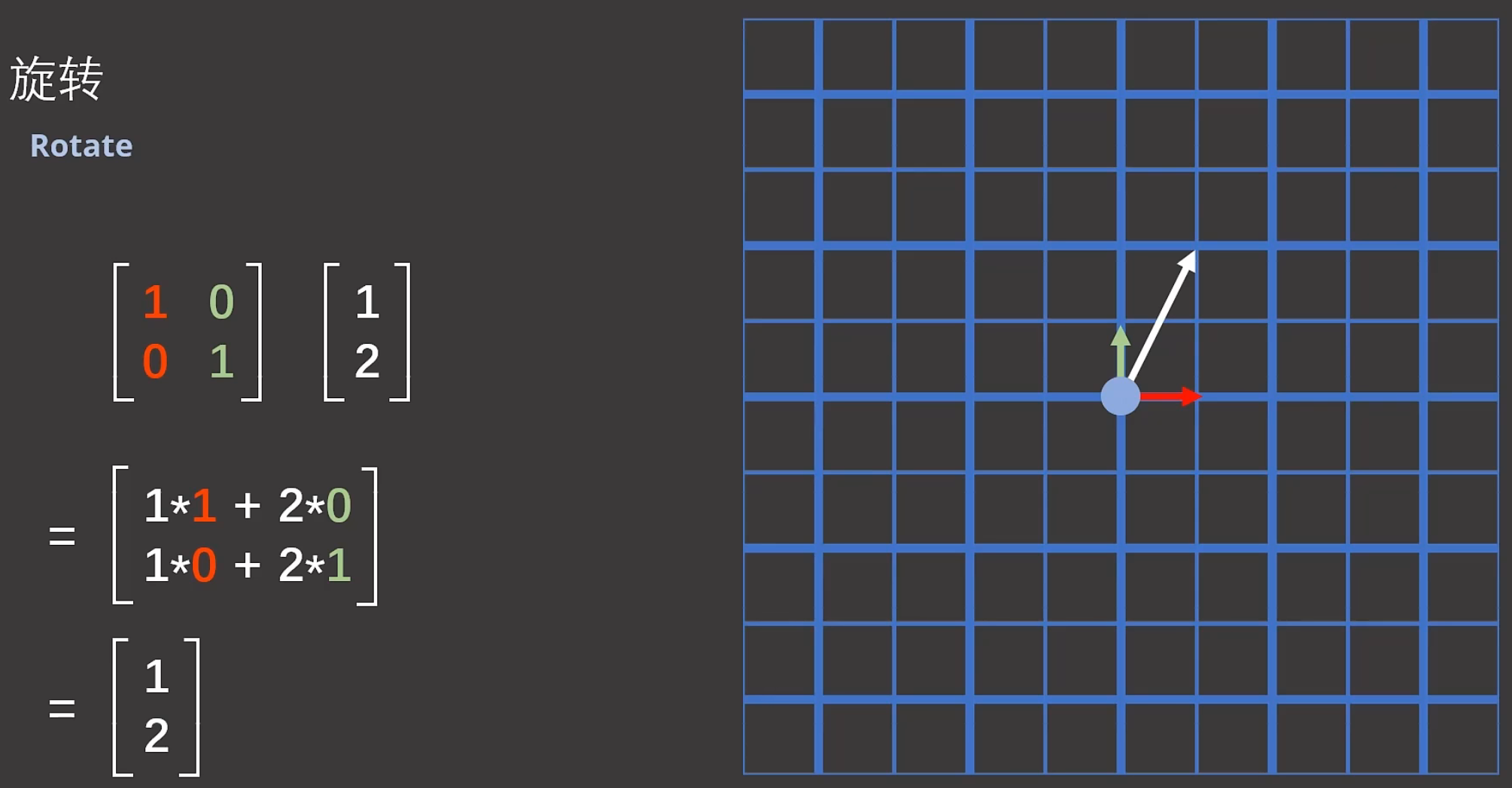
坐标系逆时针旋转90°后,新的基向量是![]() 和
和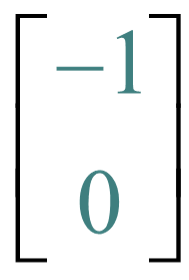 :
:

注解:
1.这其实是个特定方向的旋转,但是我们平时做的旋转很多情况下是有一定度数的旋转。这就需要知道一般的旋转公式。
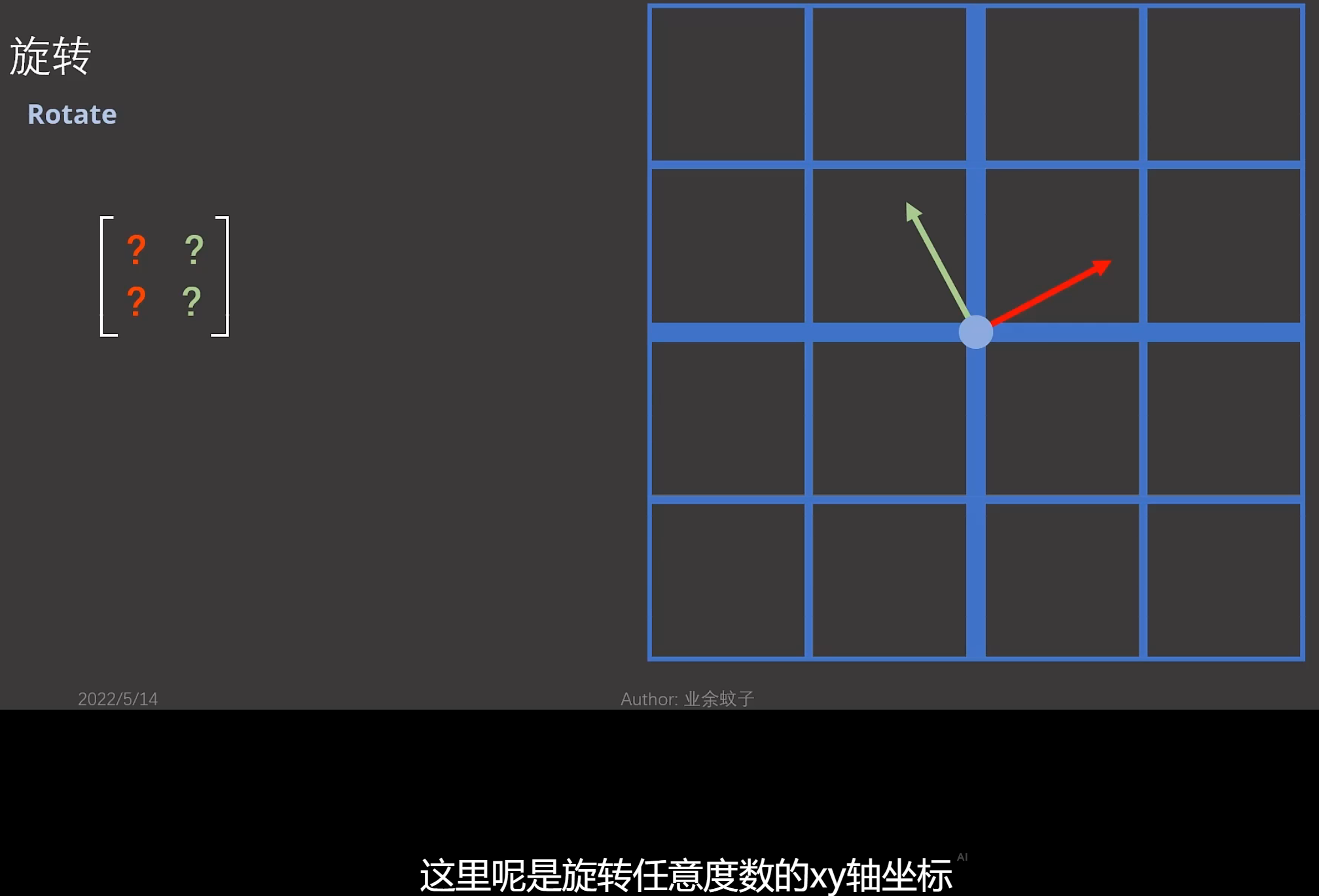
注解:
1.只要知道新的基的坐标就行了,即新的基在原始坐标系的中的坐标(x轴和y轴上的值),就知道旋转矩阵的样子了。
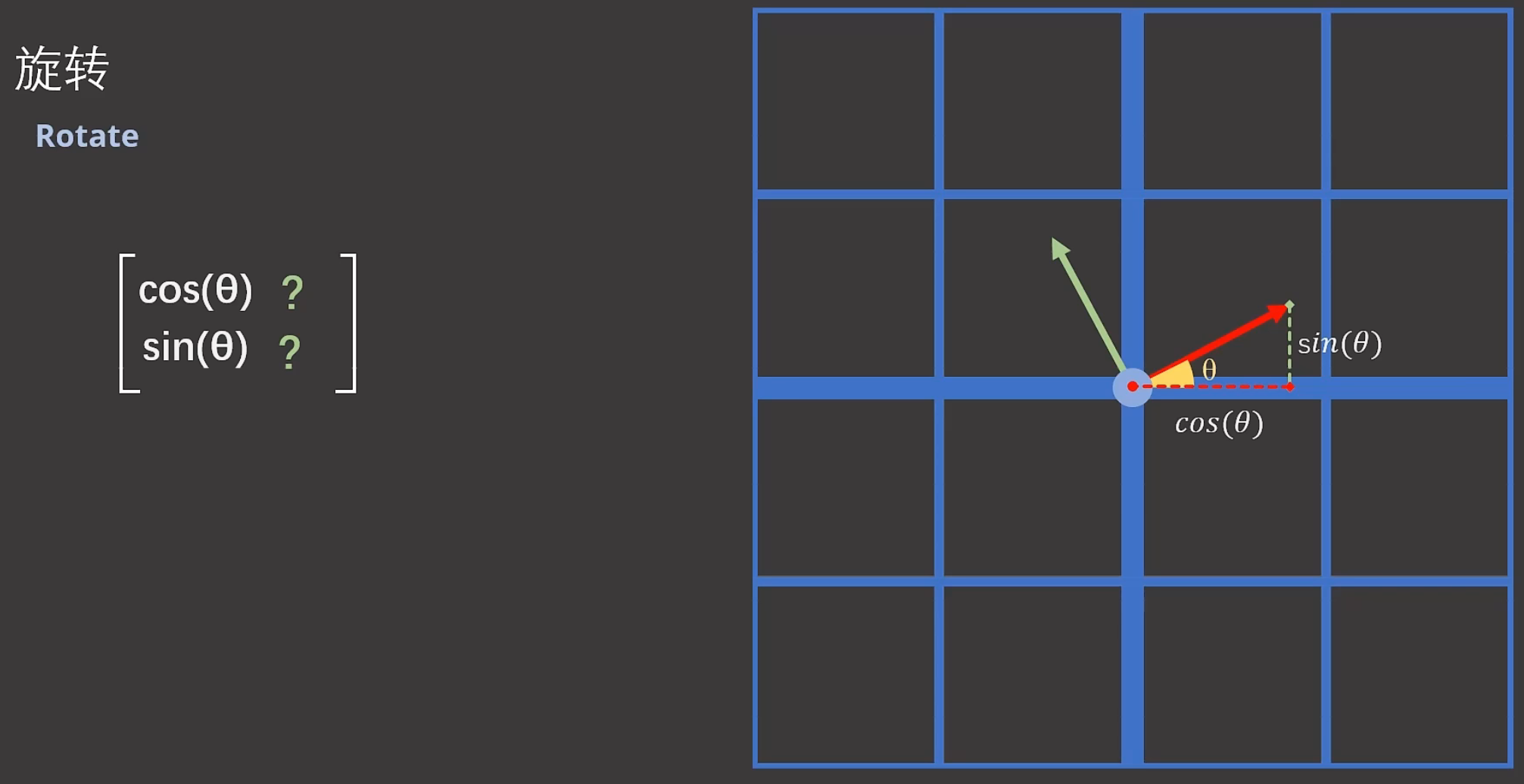
注解:
1.旋转的度数θ是已知的,因为是给定的度数。
2.新的第1个基向量是一个单位向量。
![]()

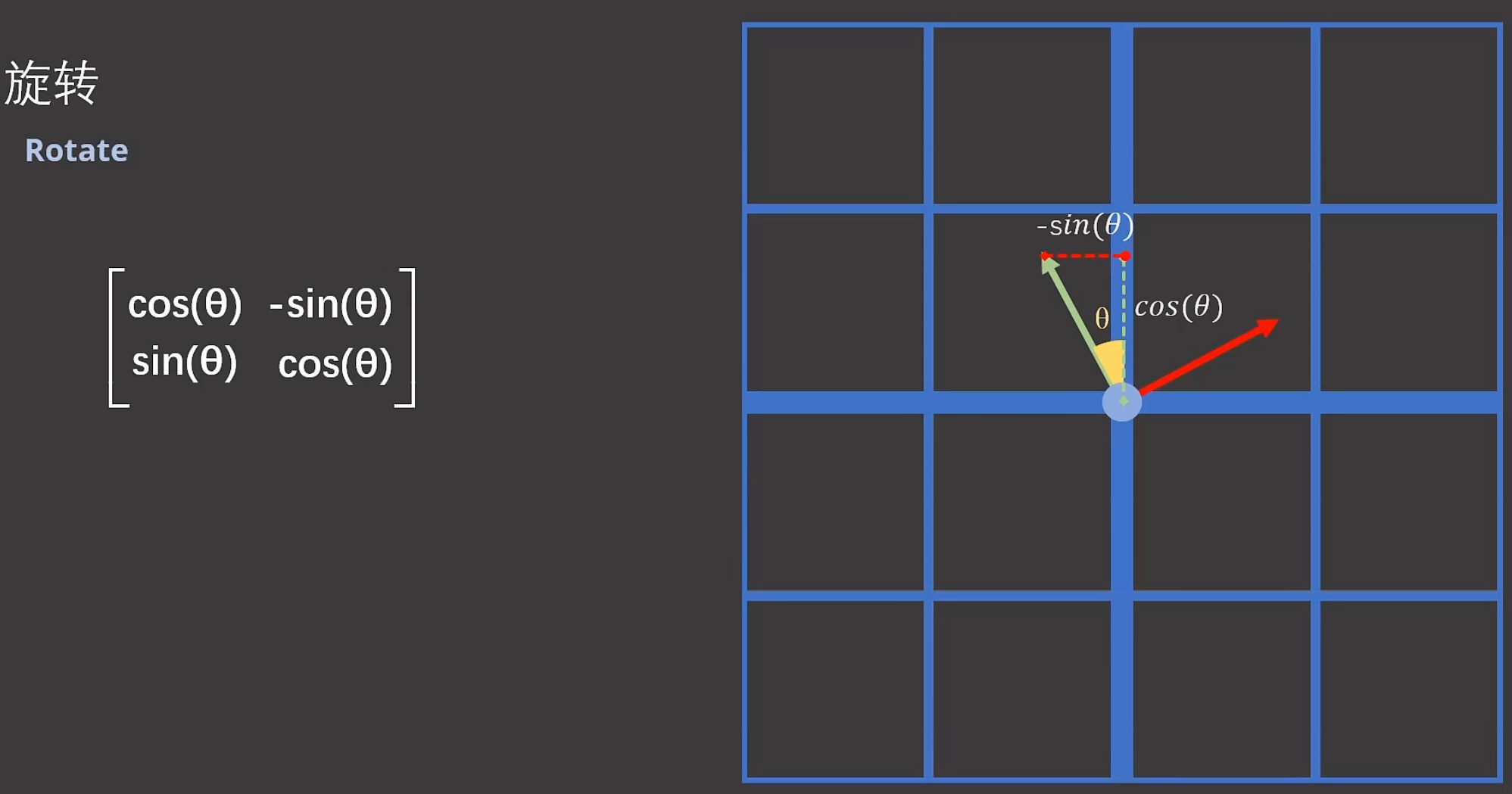
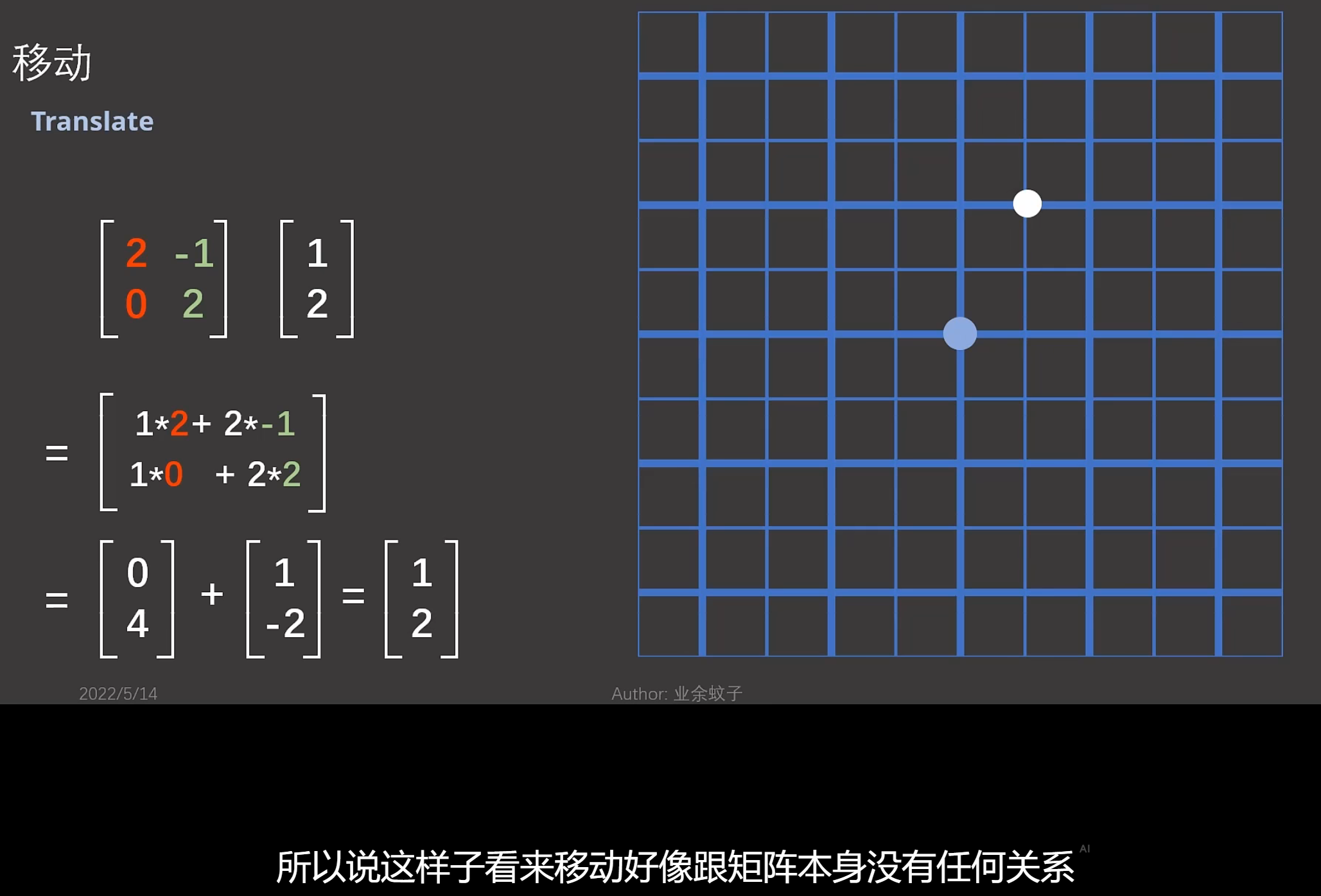
![]()
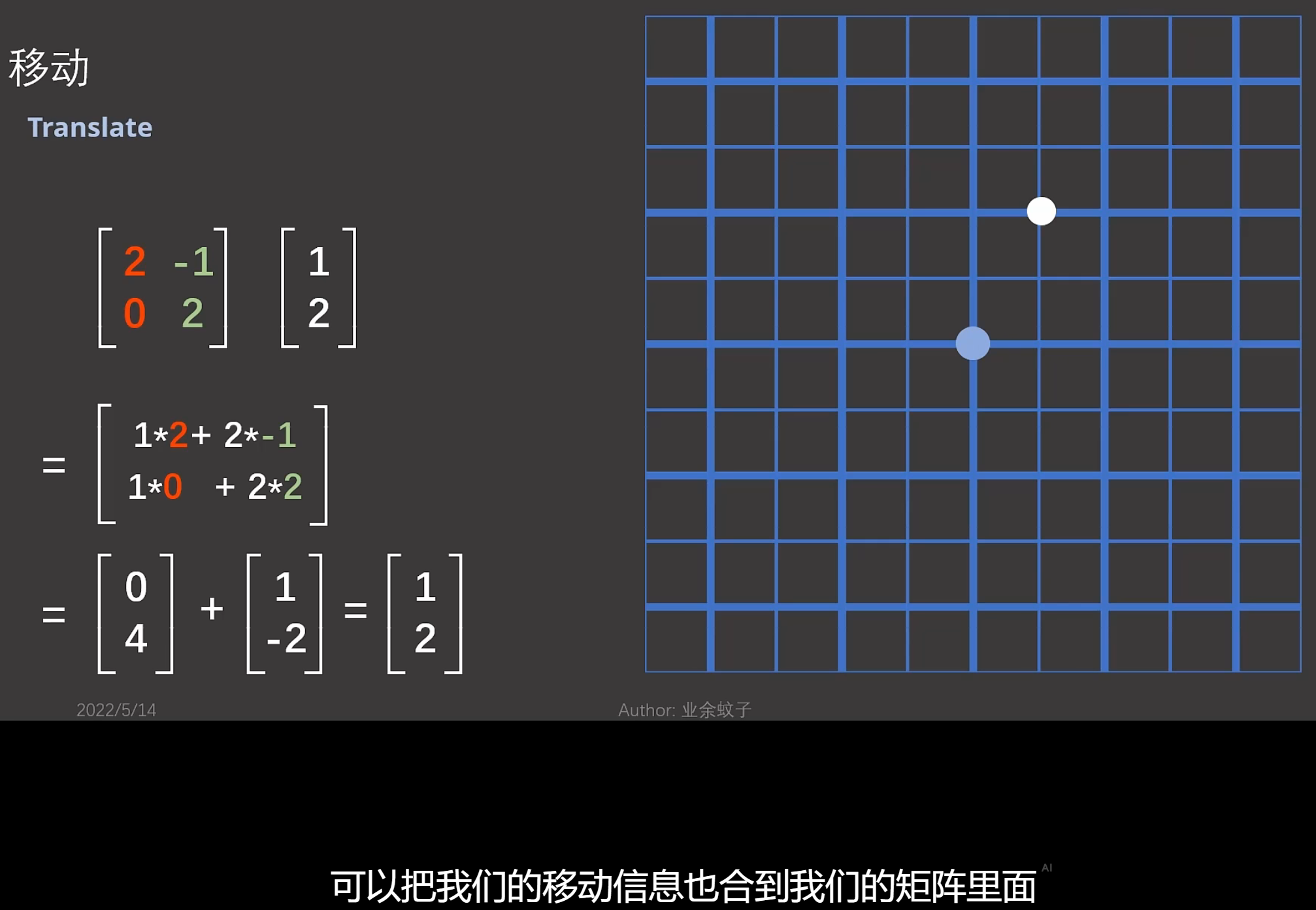
![]()




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
2021-05-19 什么叫做cover letter?
2019-05-19 OTSU大津法对图像二值化