【线性代数的本质】线性空间、基向量的几何解释

【线性代数的本质】线性空间、基向量的几何解释_哔哩哔哩_bilibili

 

注：

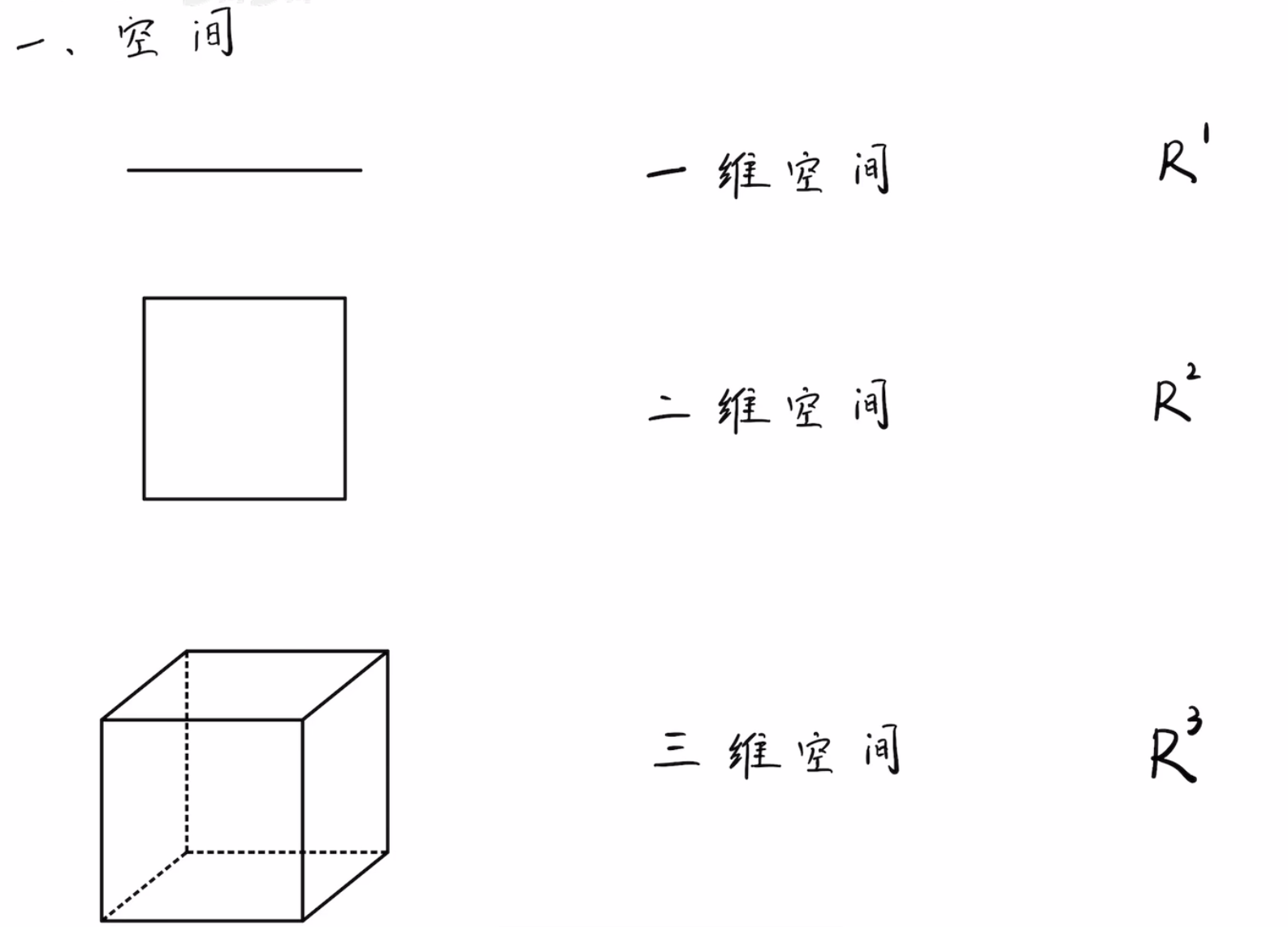
1.学习新事物的时候，要和之前熟悉的事物进行类比理解。

 

注：

1.当然，向量的坐标和点的坐标是一样的，向量的坐标就相当于是点的坐标了。

 

 

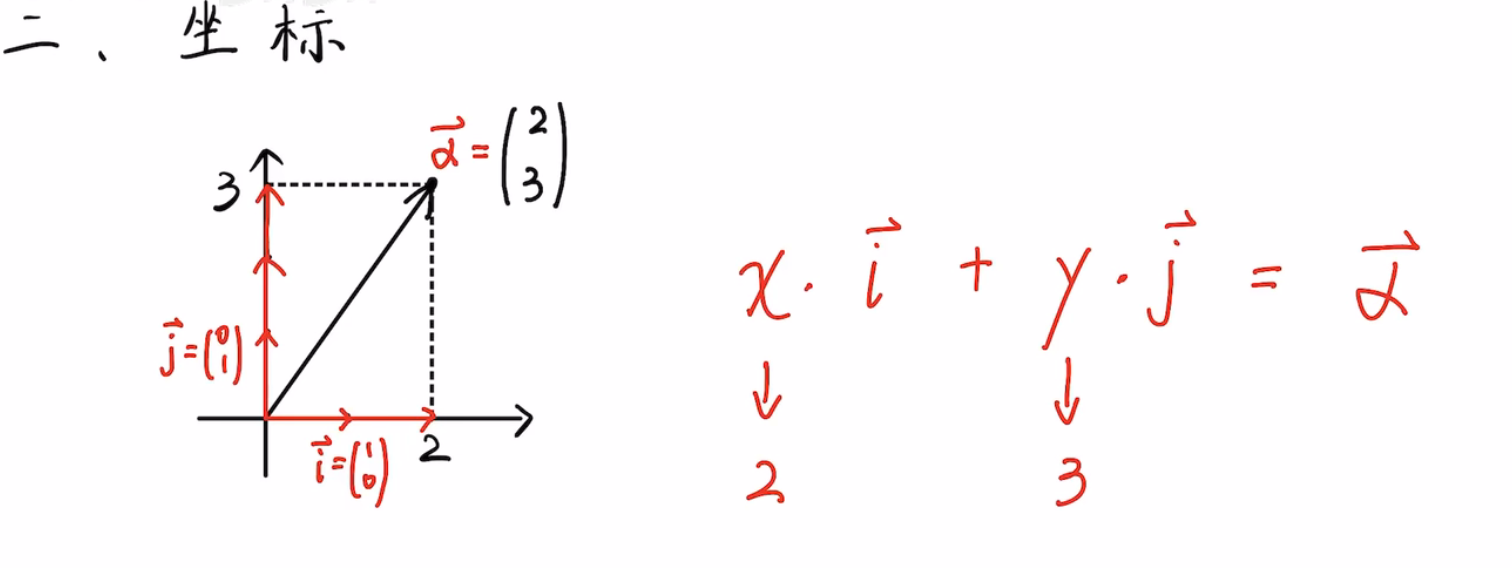
注：

1.二维空间中的所有点（所有向量）都可以通过单位向量i和j的线性组合表示出来。那么，就说单位向量i和j可以表示整个二维空间。换言之，单位向量i和j张成了二维空间。

 

注：

1.基向量组也可以叫做基。

注：

1.α和β能不能表示整个二维空间呢？

答：能。只要是不相关的两个向量都能作为一组基表示整个二维平面。

2.规范正交基的概念：

3.最常用的规范正交基就是i,j.

 

 

 

注解：

1.向量或者图形、图像左乘一个（二维、三维）矩阵相当于是对向量、图形或者图像做一个空间变换。简而言之，乘上一个矩阵相当于是做空间变换。

2.空间是可以有无限多组基的。可以是左边的i,j，也可以是右边的α,β。每一组基相互之间是否可以转换呢？

答：能。

如何转化？

答：左边的i,j，和右边的α,β之间从图像上看，其转化就是旋转，拉伸。而旋转、拉伸这些变换在线性代数（数学）中是通过乘上一个（旋转、拉伸）矩阵P来实现的，如下图：