【线性代数的本质】特征值/特征向量的几何涵义

【线性代数的本质】特征值/特征向量的几何涵义_哔哩哔哩_bilibili

一般，教材上的定义是:

Aλ=kλ

λ就是矩阵A的特征向量，k就对应特征向量的特征值。

空间变换的概念

我的理解就是：参考系发生变化导致空间发生了扭曲或者变形。

正常的参考系是由单位向量(1,0)和单位向量(0,1)组成的参考系，但是下面这个也可以是个参考系：

 

 

 就是说：

任何线性无关的2个向量都可以作为基向量，组成一个参考系，因为任何线性无关的2个向量（的线性组合）都可以表示出来平面上的所有向量。或者说，平面上的任一向量都可以由线性无关的2个向量线性表示。

 

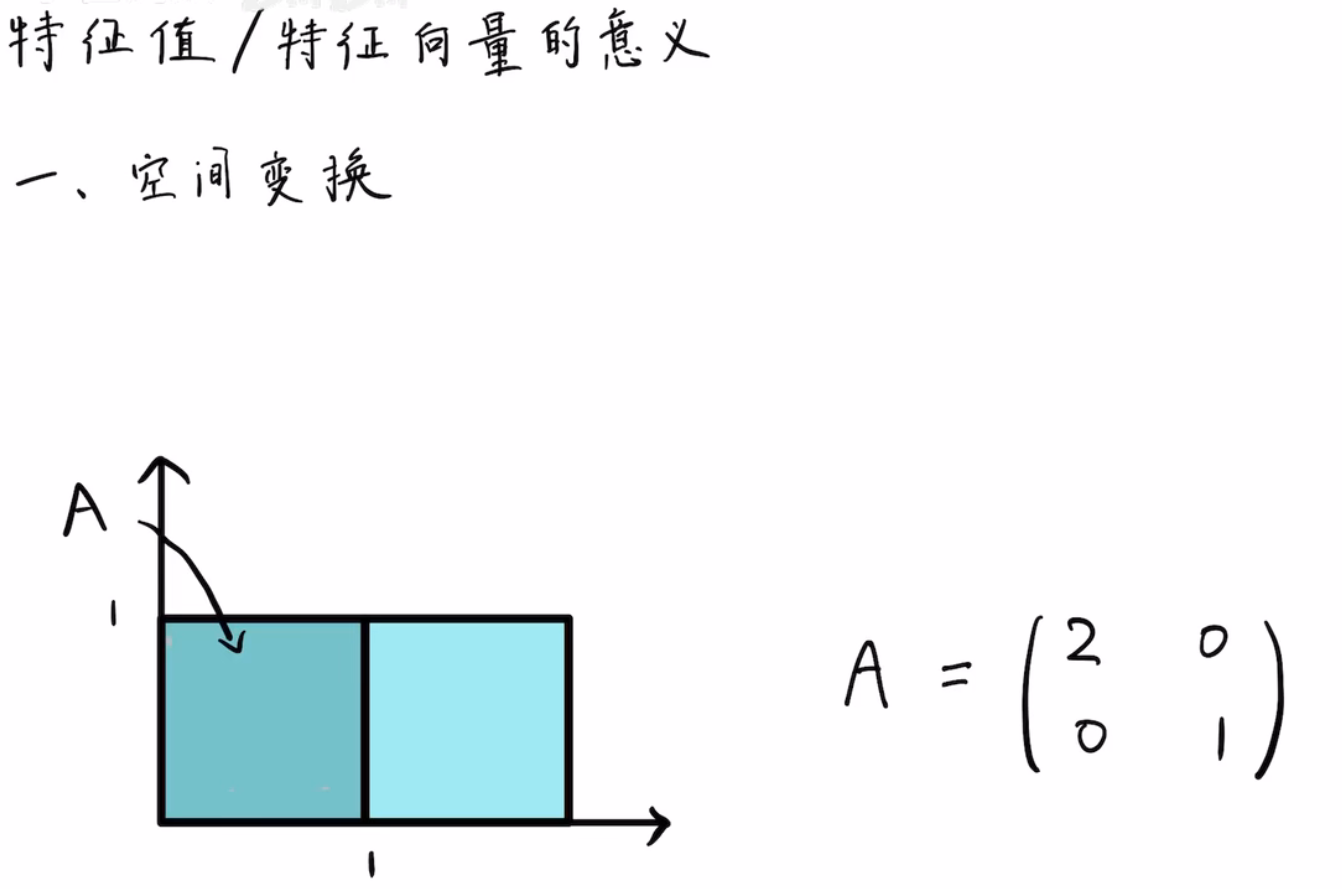
 注：

1.矩阵的乘法就意味着：

在空间中做变换-旋转、拉伸。

2.A矩阵作用于一个图形，就意味着将此图像在水平方向拉伸为原来的2倍，这个是拉伸变换。

 

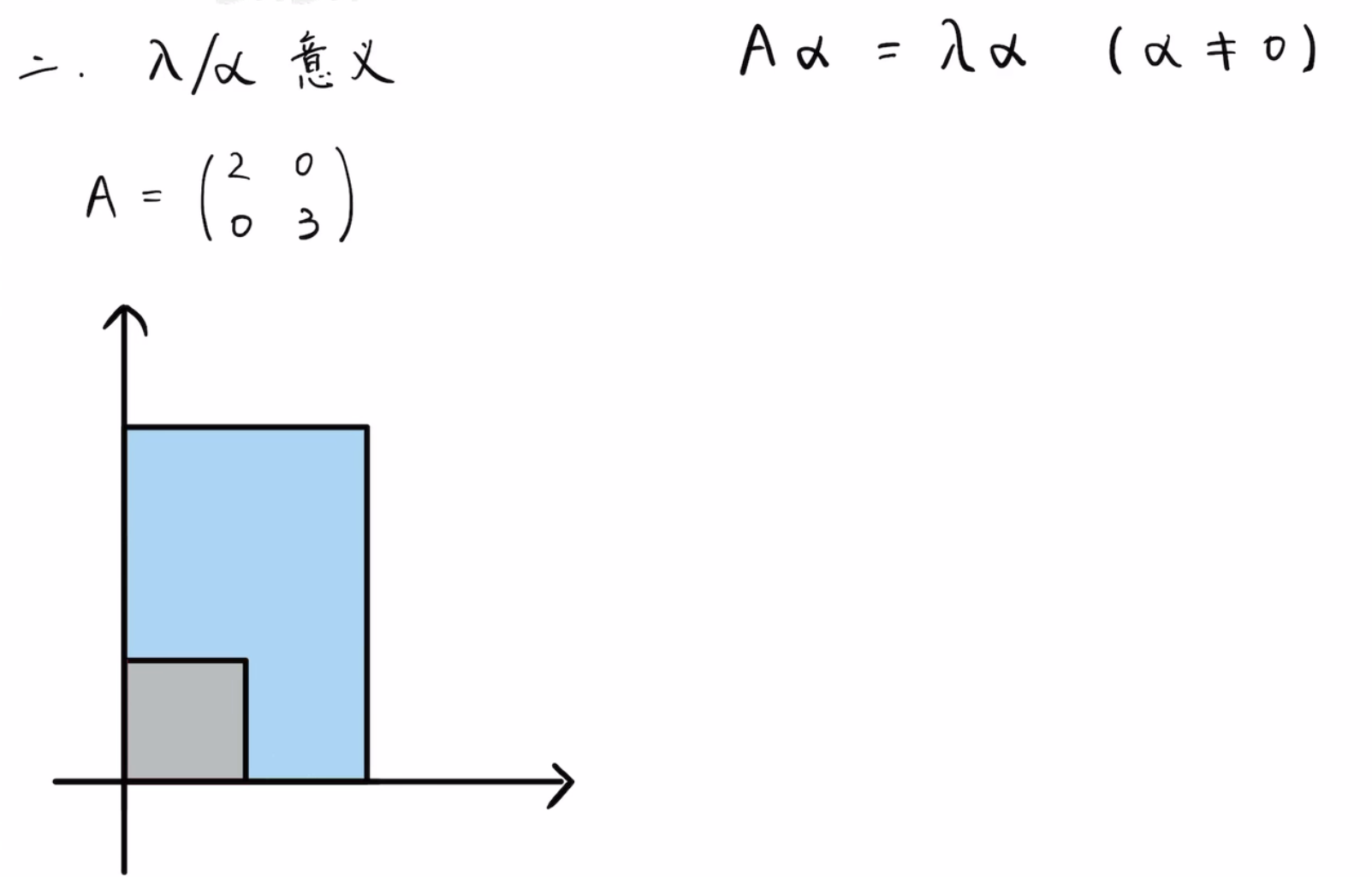
 注：

1.λ和α给人的感觉就是他们反映了矩阵A的某些特征、特质。

2.α≠0，说明0向量不能当作特征向量。

 

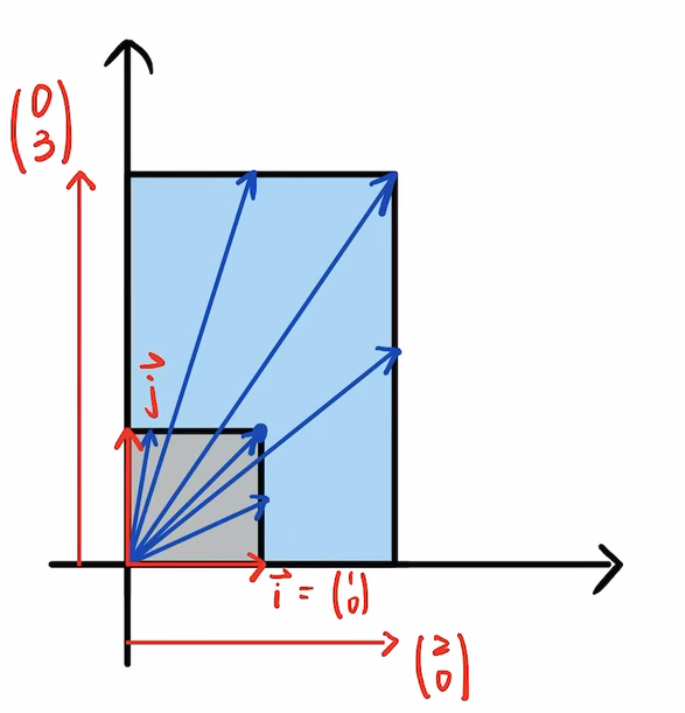
3.矩阵A会把边长为1的小正方形拉伸成一个长宽分别为2和3的矩形。

 

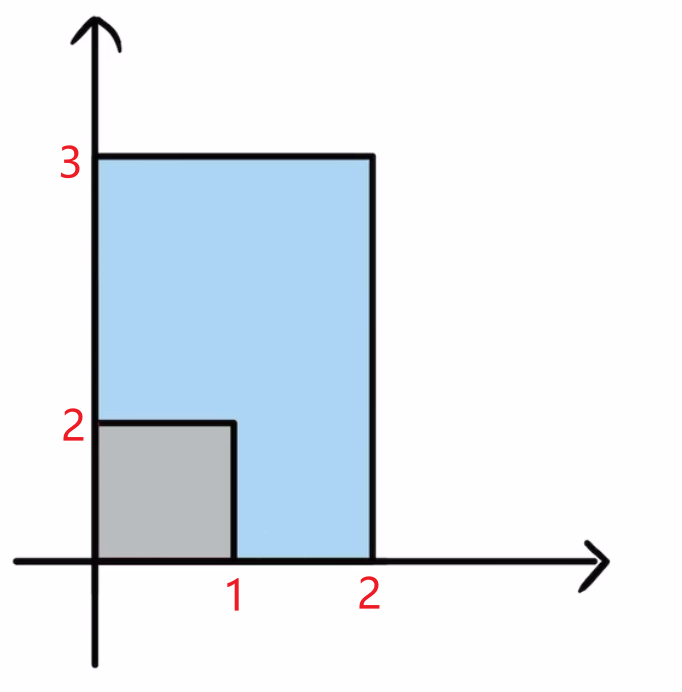
4.(1,1)这个向量在A矩阵的作用，变成了(2,3)这个向量。

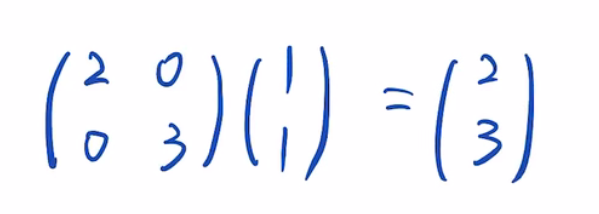
这个变换使得原来的向量(1,1)的方向和大小都发生了改变。

 

 

 

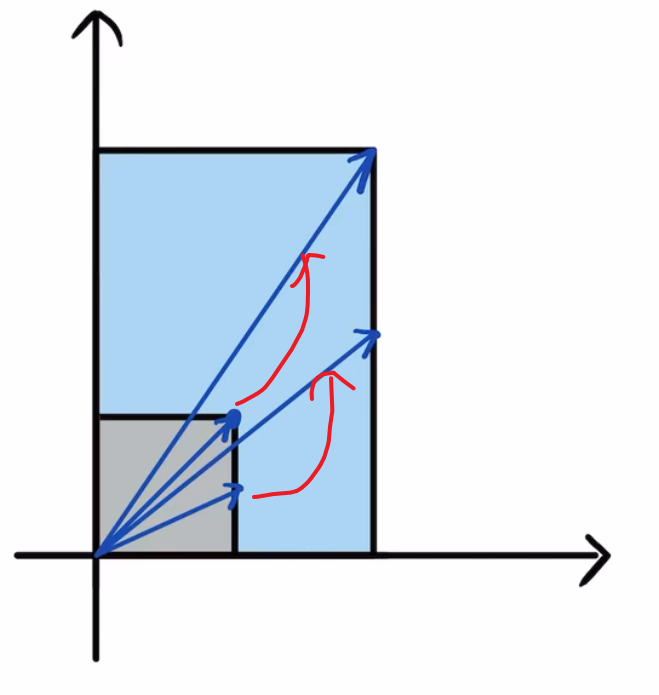
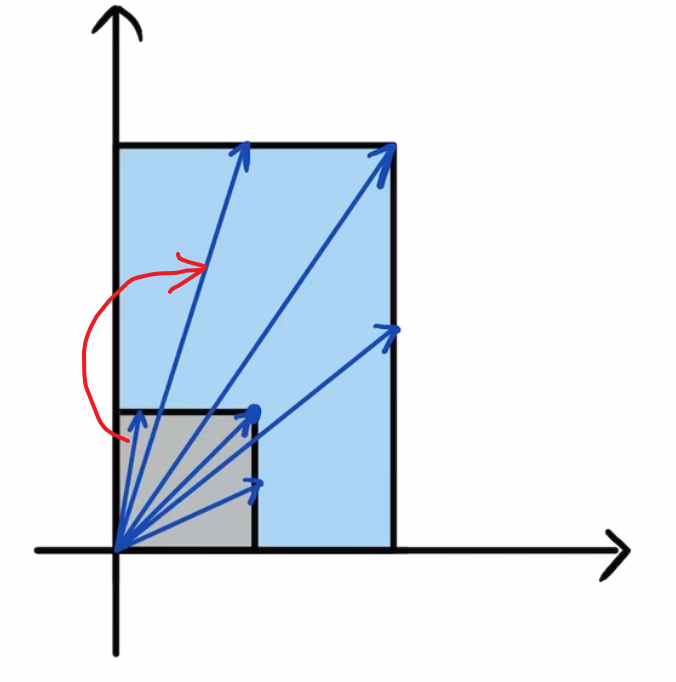
同样的，向量(1,1/2)会变成(2,3/2).

5.思考：有没有向量，它的方向没有发生变化呢？显然是有的，他们是：

 

 

 

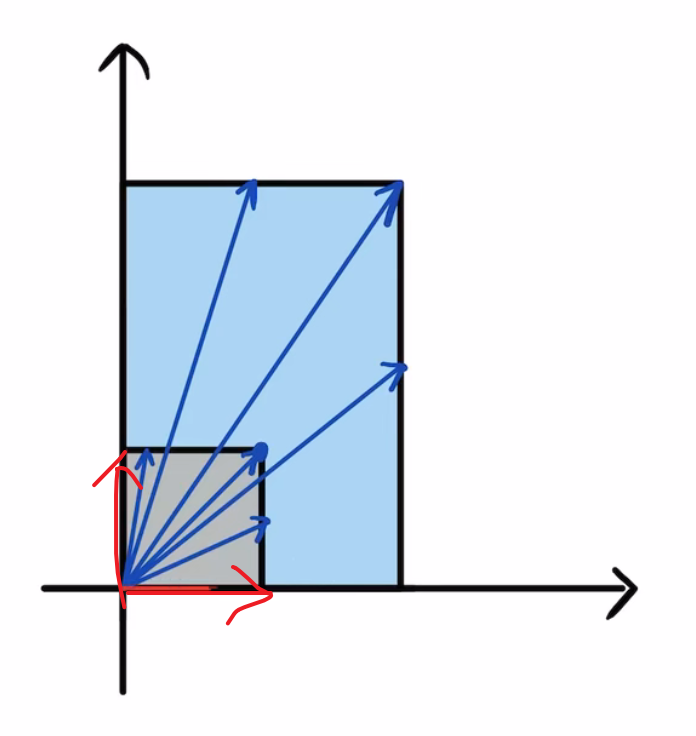
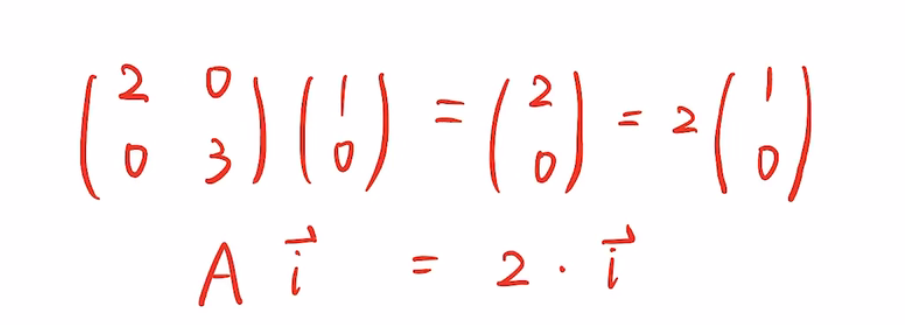
所以，i是矩阵A的一个特征向量，2是对应的特征值。

j=(0,1)向量在A的作用下，方向也没发生改变，所以它也是A的一个特征向量，3是对应的特征值。

 

 

 

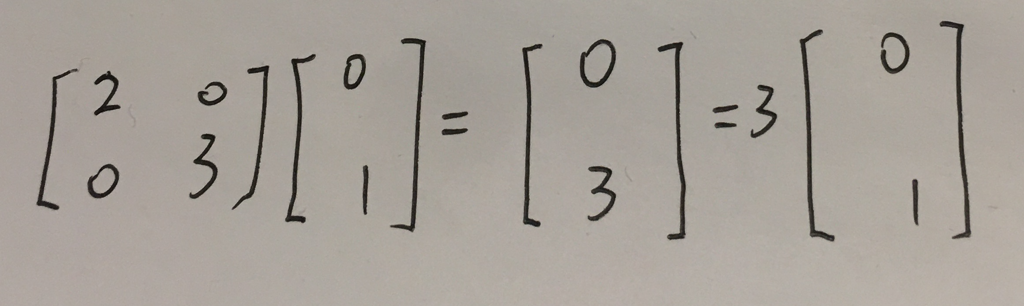
6.除了i向量和j向量外，与i向量共线的向量都是A的特征向量，与j向量共线的向量也都是A的特征向量。

7.特征向量的定义：

某些向量在使用A矩阵进行空间变换前后，没有改变方向的那些向量就是特征向量。A矩阵实际上建立了一个新的参考系。

8.特征向量和特征值的几何含义

 

特征向量指明了方向不发生变化的那些向量的拉伸的方向，特征值表示了拉伸的倍数，这即是特征向量和特征值的几何含义。

9.有些矩阵作用在向量上，让向量逆时针旋转90°。这样的矩阵称为是旋转（变化）的矩阵。

 

 

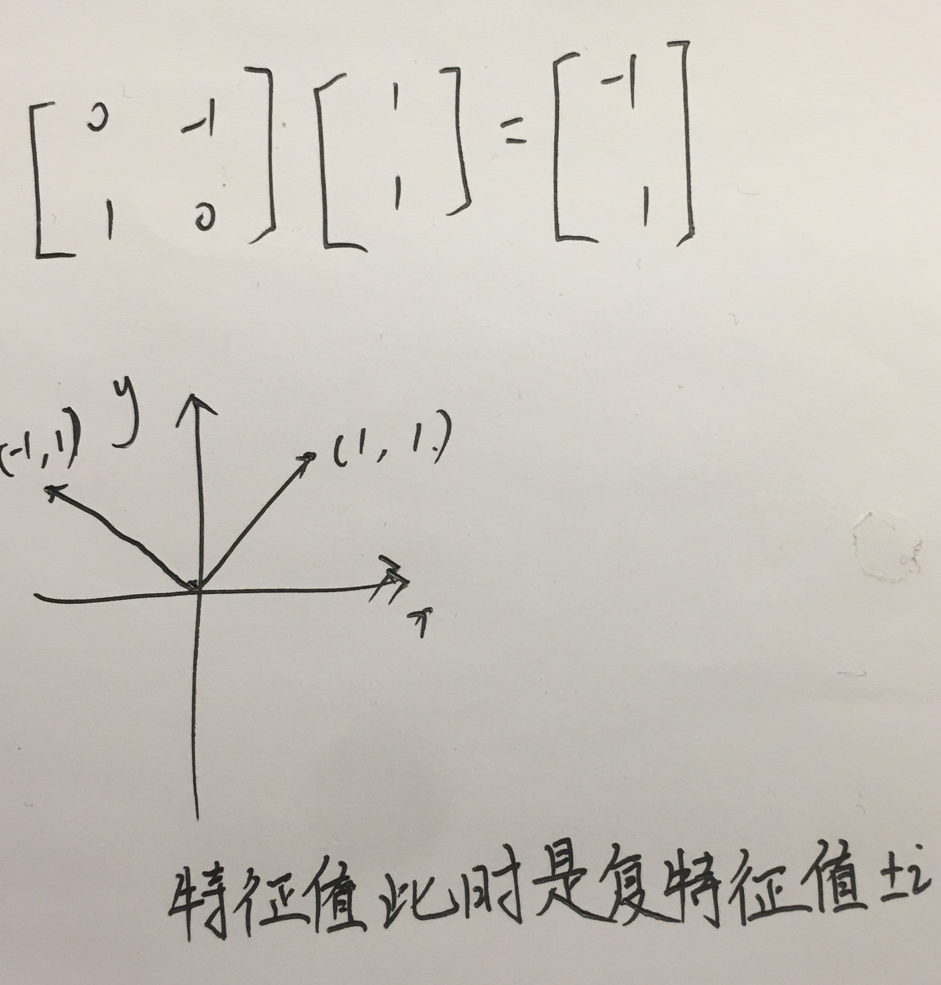
10.复特征值和旋转有什么关系呢？或者说为何会对应的呢？

 

 

 

 

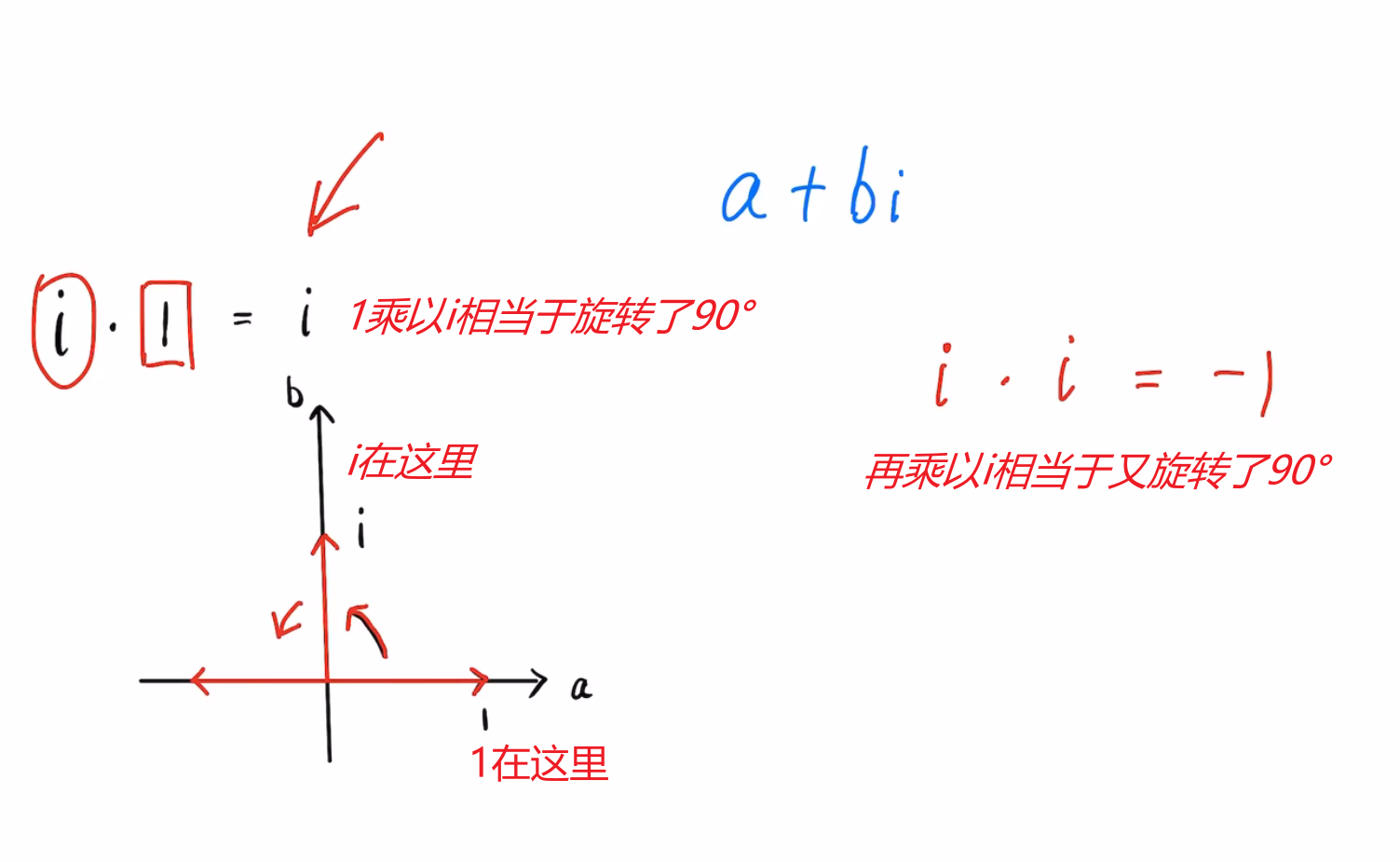
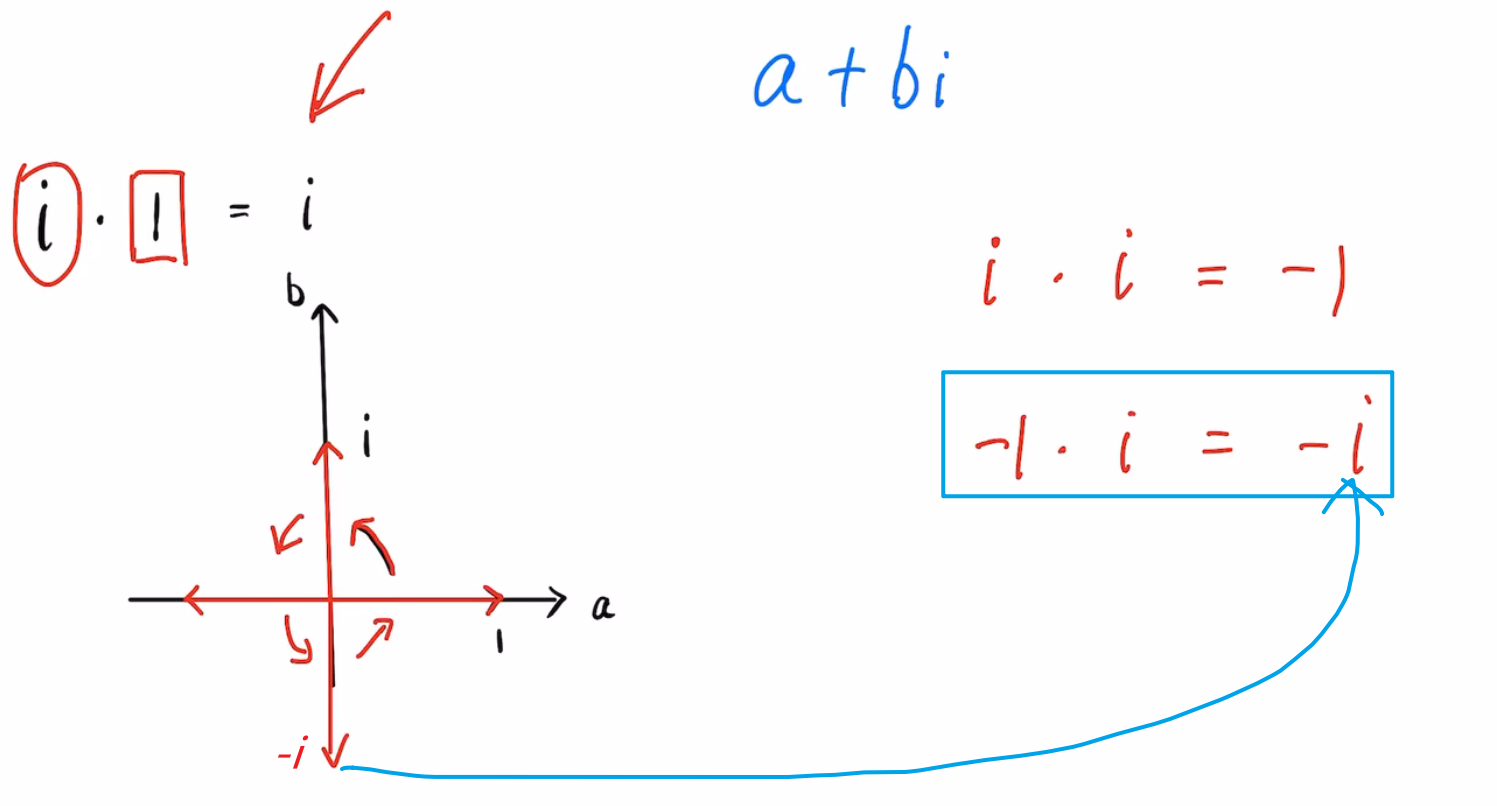
横轴和竖轴分别表示实部和虚部。

所以，复数往往和旋转有关系。