分段线性插值

首先，科普一下插值的含义：在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

插值的方法有很多：拉格朗日插值法，牛顿插值法，分段线性插值，样条插值等，每种插值方法都有自己的优缺点。

今天，我们介绍的是比较简单的分段线性插值方法，分段线性将每两个相邻的节点用直线连起来，如此形成的一条折线就是分段线性插值函数。计算点的插值时，只用到左右的两个节点，计算量与节点个数n无关。

假设两个节点为（x1，y1）和（x2，y2），则该区间上的一次线性方程为：

 

 

 

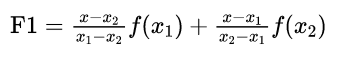
下面讲解一下证明过程（证明过程很简答，大家在初中就学过了）：

 

 

 

 

 

 

 

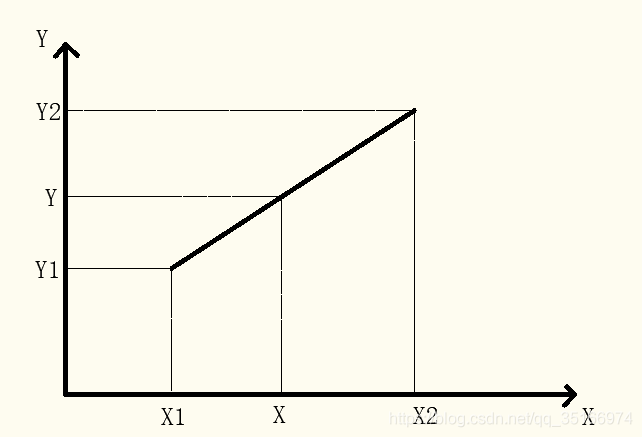
以上就是分段线性插值的原理，可以看出原理十分简单。分段线性插值运算量较小，插值误差较小，插值函数具有连续性，但是由于在已知点的斜率是不变的，所以导致插值结果不光滑，存在角点。

下面给出分段线性插值的MATLAB实现函数：

function y_output = piecewiselinearinterp(x,y,x_input)
%该函数实现分段线性插值
%x为已知的数据点
%y为已知的数据点
%x_input为待插值的横坐标
%y_output为插值后的到的结果
%The Author:等等登登-Ande
%The Email:18356768364@163.com
%The Blog:qq_35166974
 
n = length(x);
nn = length(x_input);
 
for j=1:nn
    for i=1:n-1
        if (x_input(j)>x(i) && x_input(j)<=x(i+1))
            y_output(j) = ((x_input(j)-x(i+1))/(x(i)-x(i+1)))*y(i)+(((x_input(j)-x(i))/(x(i+1)-x(i)))*y(i+1));
        end
    end
end

 

函数运行结果是：

 

 

 

 

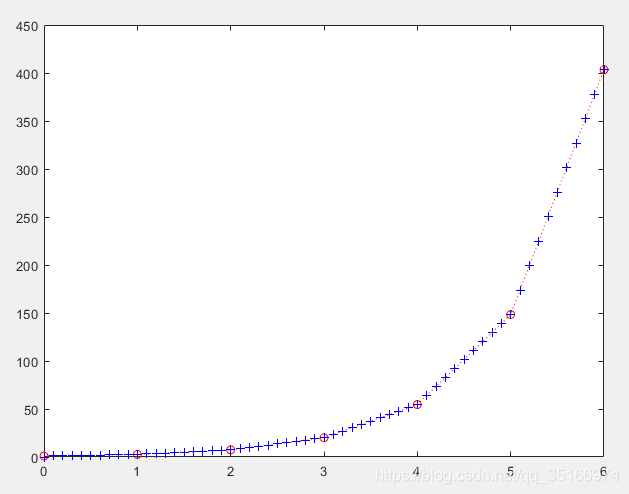
从运行结果可以看出，插值总体趋势是正确的，但是存在着很多角点，当节点越多时，插值效果会越好。
————————————————
版权声明：本文为CSDN博主「等等登登-Ande」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_35166974/article/details/90115563