病态方程的例子
从零开始几何处理:函数拟合 - 知乎 (zhihu.com)
前言
之前学完了 GAMES102,现在打算以 101 类似的形式,以作业为单位整理一下涉及的知识。
不过明显感觉到 102 涉及的知识更杂,包括函数拟合、离散微分几何,以及后面的三维重建等知识,后面有机会的话可以单独写个总结(挖个大坑)捋一遍。
同样尽我所能写的简单易懂点,如有错误欢迎指出……
引入
函数拟合这个词并不陌生,高中时我们就学过最小二乘法线性拟合二维点,这就是一个函数拟合的例子。
函数拟合,顾名思义,就是有一对数据点,我们要根据这些数据点找到一个函数,来描述数据集。
在实际生活中,许多应用也满足这一条件,比如三维重建就是用激光雷达等扫描仪采集数据后,再找到一个表面(函数)来拟合这些数据点。
函数拟合通常分为两大类:插值问题、逼近问题。插值问题限定函数必须经过那些数据点,逼近问题则不一定。
下面来分别介绍一下。
插值问题
首先来定义一下插值问题:已知离散的数据点集,构建(估计、寻找)一个新的数据点集。
换句话说,给出 m 个点 ,求一个函数
作为点集的估计,使得满足
。我们可以通过函数 f 来获取新的点集。
函数空间
函数 f 是什么?我们并不知道。它有可能是多项式函数,有可能是三角函数的组合,有可能根本不存在解析式。我们的目标是找到一个比较好的估计。
一般来说,为了更方便地寻找函数 f,我们需要规定一个函数空间,在这个空间内寻找 f。和线性代数里的基向量类似,函数空间的若干基底称之为基函数,该函数空间内的任意函数都是基函数的线性组合。
一个栗子:多项式
一个最常用的函数空间就是多项式函数空间,基函数为
假定函数 f 是一个 n-1 次多项式,那么 f 可以写为
我们的目的是求得所有的 。换句话说,我们求解的是如下的线性方程组
其中
注意到 G 是一个 的矩阵。假设方程之间线性无关,由线性代数知识可知,求解线性方程组需要比较未知数个数 n 和方程个数 m 的大小:
- 若 m > n,即插值问题中给定点数比未知数要多,则无解。
- 若 m = n,则有唯一解。
- 若 m < n,则有无穷解。
值得一提的是,对于多项式函数的插值,当 m = n 时,存在一种快速求解 f 的方式,称为拉格朗日插值法,如下
即构造了 ,使得
。所以多项式插值可以在
下完成。
任意函数空间
事实上,对于任意函数空间,假设基函数为 ,
可以写作
类似于上述,插值问题即求解 中的
,其中
与上述类似,而
解的情况与上述讨论类似,不同的是,非多项式函数空间可能并不存在像拉格朗日插值一样方便的求解方法。
另外,在实际操作中,如果出现 m<n 的情况,即方程个数(给定数据点个数)小于未知量个数时,可以使用某些方法添加约束(添加方程/数据点)使得满足 m=n。例如取平均等。
多项式函数空间是万能的吗?
首先看一个问题:既然我们有了拉格朗日插值法,可以快速插出任意的多项式,那么其他函数空间还有存在的必要吗?
答案当然是有必要的。事实上,多项式函数空间存在一些问题。
注:本小节中假设 n=m,即插值点数(方程数)等于基函数个数
我们已经知道,插值问题等价于一个线性方程组求解问题,而线性方程组的求解问题又等价于矩阵求逆问题。
然而在实际操作中,逆矩阵可能遭遇数值精度等问题,导致难以求解。例如下图所示的病态矩阵,对其做很小的扰动便导致了解的剧变

可以把每个方程看做一个超平面,求解方程组变成若干超平面的求交问题,如果超平面接近于平行,那么很小的扰动便会导致解发生巨大的变化。
衡量矩阵的病态程度可以使用矩阵的条件数,即最大与最小的特征值之比,越大表明某一个基底的支配程度越高,则对扰动越敏感。
在插值问题中,系数矩阵只与基函数和给定数据点有关。如果基函数选的不好,那么可能会导致病态问题。
多项式插值的系数矩阵是病态的。因为多项式插值的系数矩阵,即范德蒙德矩阵,的条件数呈指数增加
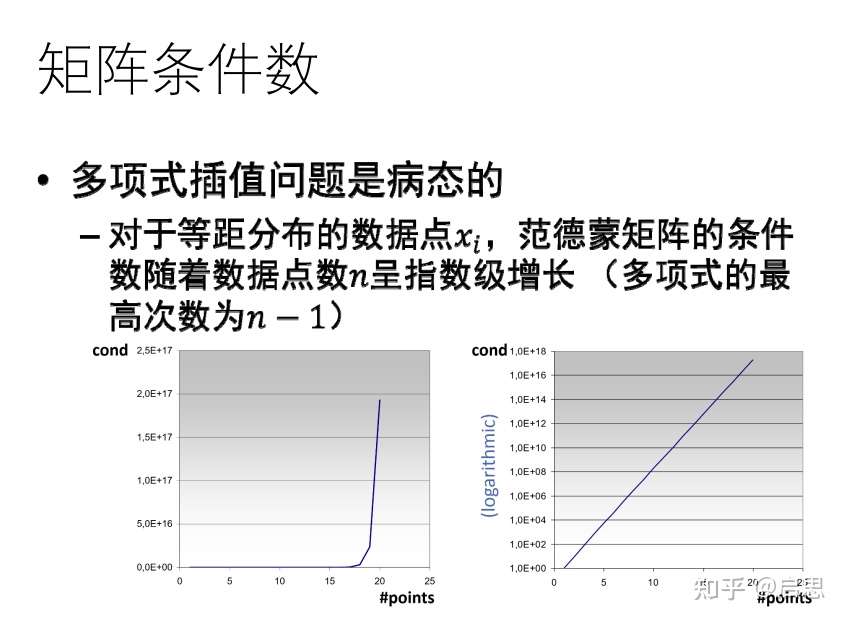
另外,我们知道任意函数都可以由无穷多的多项式函数任意逼近,但是在实际应用时,我们不可能使用无穷多个基函数。我们希望,在使用有限基函数时,随着基函数(插值点数)的增加,插值函数逐渐逼近于目标函数。
然而,多项式插值具有强烈的振荡现象,逼近的过程并不稳定。这使得我们对插值函数的可信度有所质疑
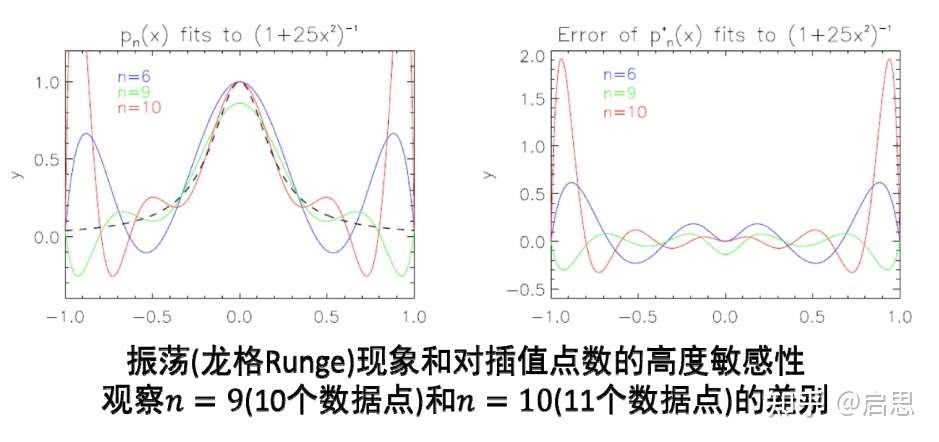
综上所述,多项式函数空间存在其本身的缺点:病态问题、振荡问题。所以我们需要更好的函数空间。
总结
插值问题,即给定若干离散的数据点,构建出新的数据点的问题。
插值问题可以认为是一种函数拟合问题,我们需要在特定的函数空间中寻找,以找到一个函数来描述数据。
在特定函数空间中寻找函数,本质上是一个线性方程组求解问题。
在实际应用中,一个好的函数空间可以让问题更容易解决。
逼近问题
在实验学科中,为了得到离散的数据点,常常使用采样等方式。通常情况下,这不可避免地带来噪声、异常值等问题,也就是说不是所有的数据点都 100% 可信。另一方面,如果必须完美拟合所有数据点,这带来的代价可能是巨大的(例如过高的参数量、计算量)。
舍弃完美拟合所有的数据点,而是寻找一个逼近(近似)函数,就是逼近问题。
更准确的,逼近问题是,给出 m 个点 ,求一个函数
使其为目标函数的一种最佳逼近(近似)。
类似于插值问题,我们仍然需要一个函数空间。
为了求解此问题,我们需要先定义“什么是最佳逼近(近似)”。事实上这并不唯一。
一个栗子:最小二乘逼近
一个广为人知的逼近算法是最小二乘法,它定义最佳逼近为:
通过将 f 写成某一组基函数的线性组合,我们可以通过求导来求解 f。沿用插值问题的符号,即求
则
事实上,在深度学习中,如果将神经网络看做一个函数空间,那么 loss 函数就是最佳逼近的一种定义。
实验
- 实现多项式函数空间的的拉格朗日插值法
- 实现高斯基函数空间的插值法
- 实现最小二乘法
- 实现最小二乘法增加正则项,即岭回归
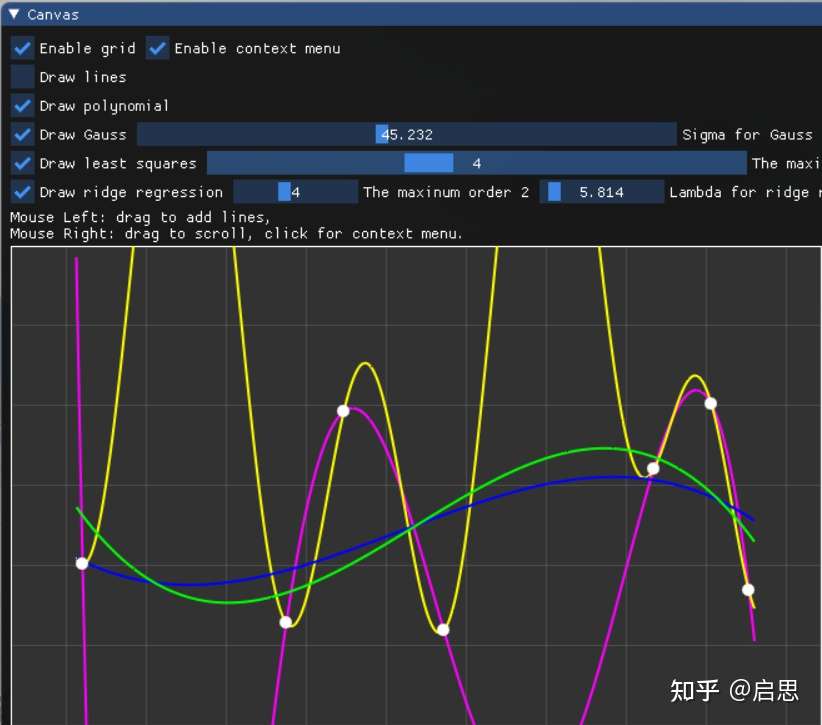
拉格朗日插值法,套公式,两个 for 即可
void drawPoly(ImDrawList* draw_list, std::vector<pointf2>& points, ImVec2 origin) {
if (points.size() <= 1) return;
auto f = [&](float x) {
int n = points.size(); // a0 + a_1*x + ... + a_{n-1}*x^{n-1}
float ans = 0;
for (int i = 0; i < n; i++) {
float tmp_fz = 1, tmp_fm = 1;
for (int j = 0; j < n; j++) {
if (i == j) continue;
tmp_fz *= points[j][0] - x;
tmp_fm *= points[j][0] - points[i][0];
}
ans += tmp_fz / tmp_fm * points[i][1];
}
return ans;
};
drawFunc(draw_list, points, origin, f, IM_COL32(255, 0, 255, 255));
}
高斯基函数,直接求解线性方程组
void drawGauss(ImDrawList* draw_list, std::vector<pointf2>& points, ImVec2 origin, float sigma) {
if (points.size() <= 1) return;
auto g = [&](int i, float x) {
if (i == 0) return 1.0f;
float xi = points[i - 1][0];
return std::exp(-(x - xi) * (x - xi) / (2 * sigma * sigma));
};
int n = points.size();
float nx = 0, ny = 0; // new point
for (int i = 0; i < n; i++) nx += points[i][0], ny += points[i][1];
nx /= n, ny /= n;
// Y=GA
Eigen::MatrixXf G(n + 1, n + 1);
for (int i = 0; i <= n; i++) {
if (i < n) { // row in [0, n-1], use origin points
for (int j = 0; j <= n; j++) {
G(i, j) = g(j, points[i][0]);
}
}
else { // row=n
for (int j = 0; j <= n; j++) {
G(i, j) = g(j, nx);
}
}
}
Eigen::VectorXf Y(n + 1);
for (int i = 0; i <= n; i++) {
Y(i) = i < n ? points[i][1] : ny;
}
Eigen::VectorXf A = G.colPivHouseholderQr().solve(Y);
// f(x) = a0 + a_1*g_1(x) + ... + a_n*g_n(x)
auto f = [&](float x) {
int n = points.size();
float ans = 0;
for (int i = 0; i <= n; i++) {
ans += A[i] * g(i, x);
}
return ans;
};
drawFunc(draw_list, points, origin, f, IM_COL32(255, 255, 0, 255));
}
最小二乘法,对求导的式子直接求解
void drawLeastSquares(ImDrawList* draw_list, std::vector<pointf2>& points, ImVec2 origin, int n) {
if (points.size() <= 1) return;
int m = points.size();
if (n >= m) return;
//return;
// G^T G A = G^T Y
Eigen::MatrixXf G(m, n);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
G(i, j) = j == 0 ? 1.0f : G(i, j - 1) * points[i][0];
}
}
Eigen::VectorXf Y(m);
for (int i = 0; i < m; ++i)
Y(i) = points[i][1];
Eigen::VectorXf A = (G.transpose() * G).inverse() * G.transpose() * Y;
// f(x) = a0 + a_1*g_1(x) + ... + a_n*g_n(x)
auto f = [&](float x) {
float ans = 0, xx = 1.0f;
for (int i = 0; i < n; i++) {
ans += A(i) * xx; xx *= x;
}
return ans;
};
drawFunc(draw_list, points, origin, f, IM_COL32(0, 0, 255, 255));
}
岭回归,和上述差不多
void drawRidge(ImDrawList* draw_list, std::vector<pointf2>& points, ImVec2 origin, int n, float lambda) {
if (points.size() <= 1) return;
int m = points.size();
if (n >= m) return;
// (G^T G + lambda E) A = G^T Y
Eigen::MatrixXf G(m, n);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
G(i, j) = j == 0 ? 1.0f : G(i, j - 1) * points[i][0];
}
}
Eigen::VectorXf Y(m);
for (int i = 0; i < m; ++i)
Y(i) = points[i][1];
Eigen::MatrixXf E(n, n);
E.setIdentity();
Eigen::VectorXf A = (G.transpose() * G + lambda * E).inverse() * G.transpose() * Y;
// f(x) = a0 + a_1*g_1(x) + ... + a_n*g_n(x)
auto f = [&](float x) {
float ans = 0, xx = 1.0f;
for (int i = 0; i < n; i++) {
ans += A(i) * xx; xx *= x;
}
return ans;
};
drawFunc(draw_list, points, origin, f, IM_COL32(0, 255, 0, 255));
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
2020-01-27 高斯滤波
2020-01-27 MATLAB的padarray函数
2020-01-27 《滕王阁序》—— 作者:王勃