常见的分布
2021.10.26

注解:
1.Ber-E1:伯努利一次实验。----投篮,掷硬币。
2.掷骰子可以转化为0-1分布,如大于等于3点记1,小于3点记成0。
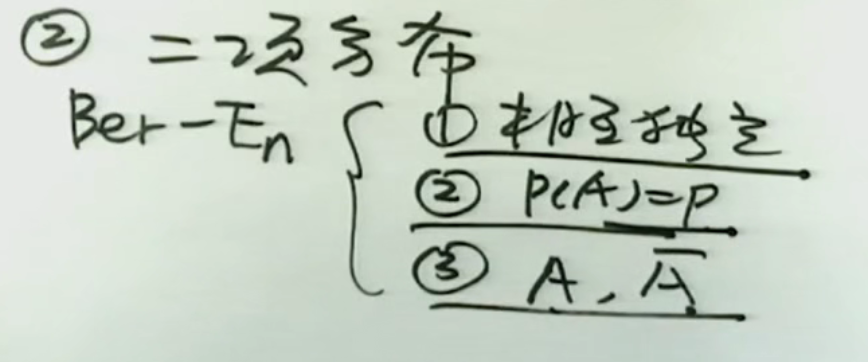
注解:
1.每次投篮相互独立;
2.每次投篮的概率不变(理想化情况);实际情况:投篮次数增加的时候,体力会下降,命中率会降低。但也有可能经验增加,命中率增加。数学上假定投篮的是机器人。
3.每次投篮只有投中,投不中两种结果。
4.重复投篮N次命中k次的概率(这是著名的伯努利二项分布的分布律):
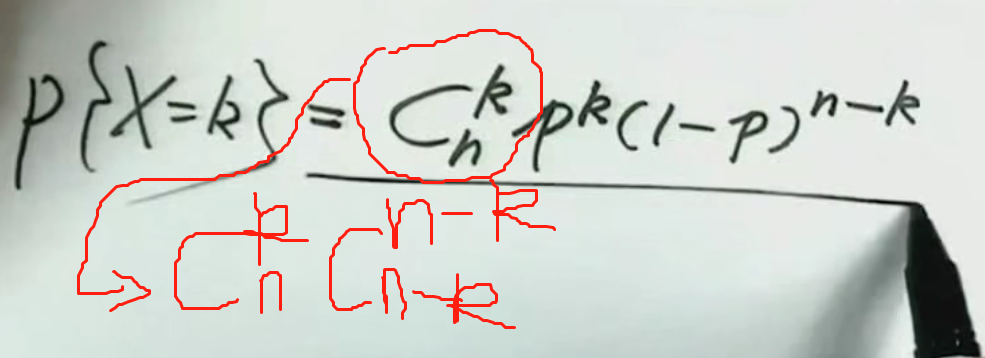
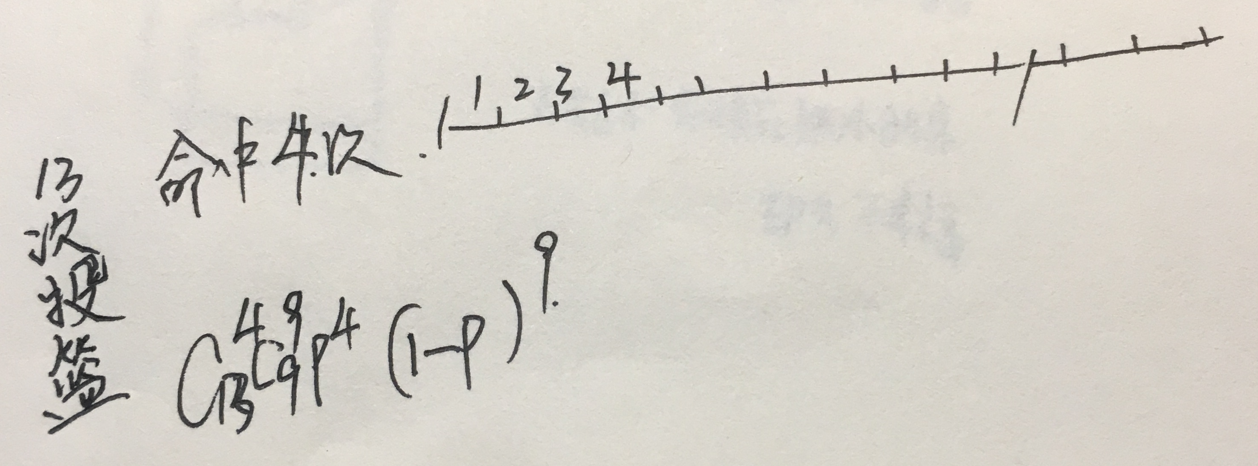

注解:
1.二项分布(伯努利n次实验)记成X~B(n,p),b:binary.
2.0-1分布只做一次实验(伯努利一次实验),所以可以写成:X~B(1,p) 
3.0-1分布就是二项分布里面的某一次。

注解:
1.实验次数无上限,但首中即停止。
2.机器第一次坏了,就停止工作了,这是谈机器的寿命问题。
3.每天都守在树下,第一天兔子没来,就意味着第一次实验没成功,直到有一天兔子来了撞树上了,拎着兔子回家了。X是等待的天数。时间是以离散的数来计算的,即第一天,第二天,第三天...知道某一天等到了兔子实验停止。

注解:
1.投篮,投k次,每次投中的概率是p。实验做k次的概率,即到了第k次才投中的概率是:

2.几何分布实际上是离散型等待分布。叫几何分布是叫错了,与几何无关。其实几何也可以理解成人生几何。
3.几何分也可以叫做离散型寿命分布。机器运转k天,坏掉了,就是机器的寿命到了。
![]()

注解:
1.取n次产品的不放回抽样,相当于任取n个。

注解:
1.十一黄金周,洛阳龙门石窟,北京故宫,游客源源不断的来参观。k是源源不断的顾客的数量。λ是源源不断的顾客来流的强度。非十一黄金周,强度弱,十一黄金周,挤的都喘不过气来,强度强。
2.源源不断的顾客的数量映射到数轴上就是(随机变量)X的取值。

注解:
1.λ等于随机变量X的数学期望。是某个时间发生的强度,是个平均值。

注解:
1.k的取值范围是正整数。
2.也常用于描述稀有事件发生的概率。
普天之下,离散分布函数有很多,这5个最重要!
下面是连续型随机变量的概率分布的情况:
连续性随机变量研究的是密度函数。不是分布律了。
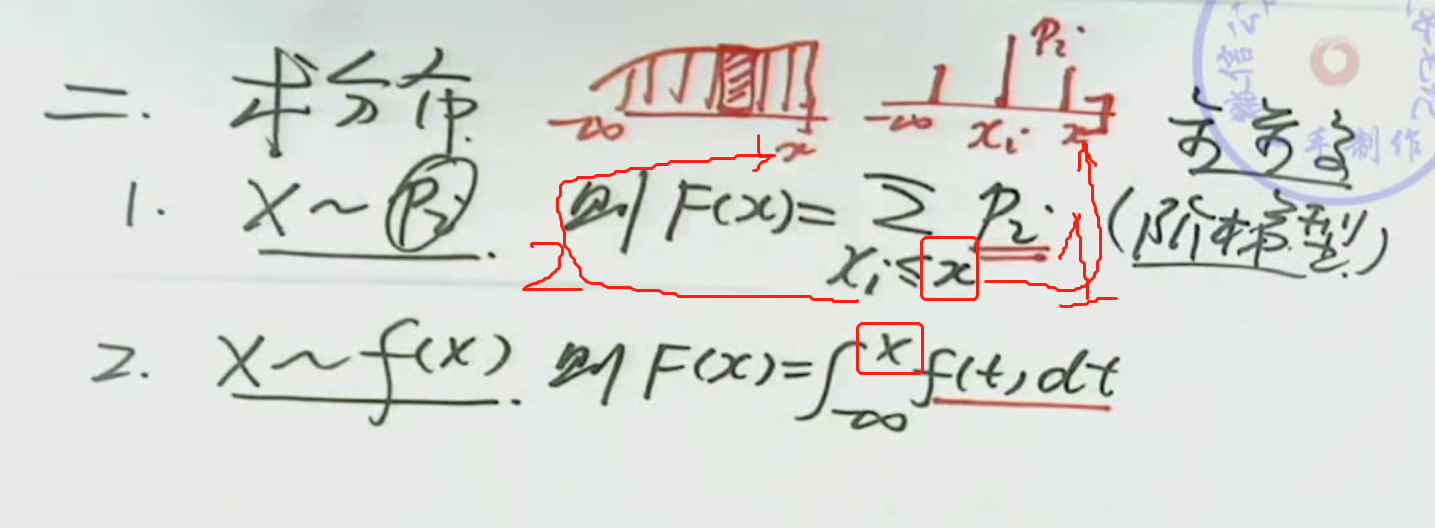
注解:
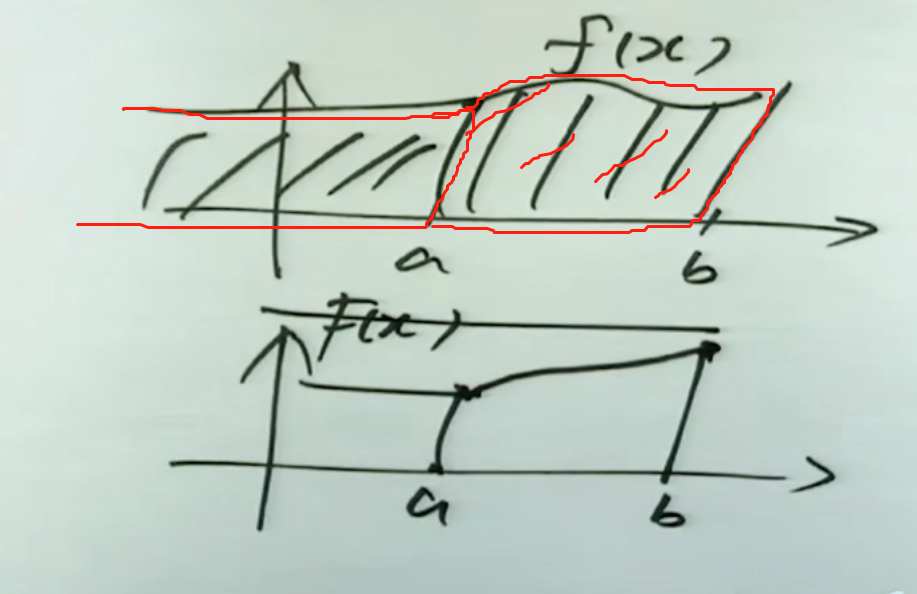
1.图中1是概率累加。2是面积累加。

注解:
1.X的概率密度函数f(x)不一定是连续的函数,是非负可积的函数。


注解:
1.随机变量X是寿命(机器的寿命,兔子的寿命...)(机器打开开始计时,人蹲在树下爱开始计时...),这个分布也是寿命分布,或者等待分布。如守株待兔,随机变量是连续时间,蹲在那里开始计时,以连续时间计时。随着时间的流逝,越往后,兔子继续活的可能性越小。
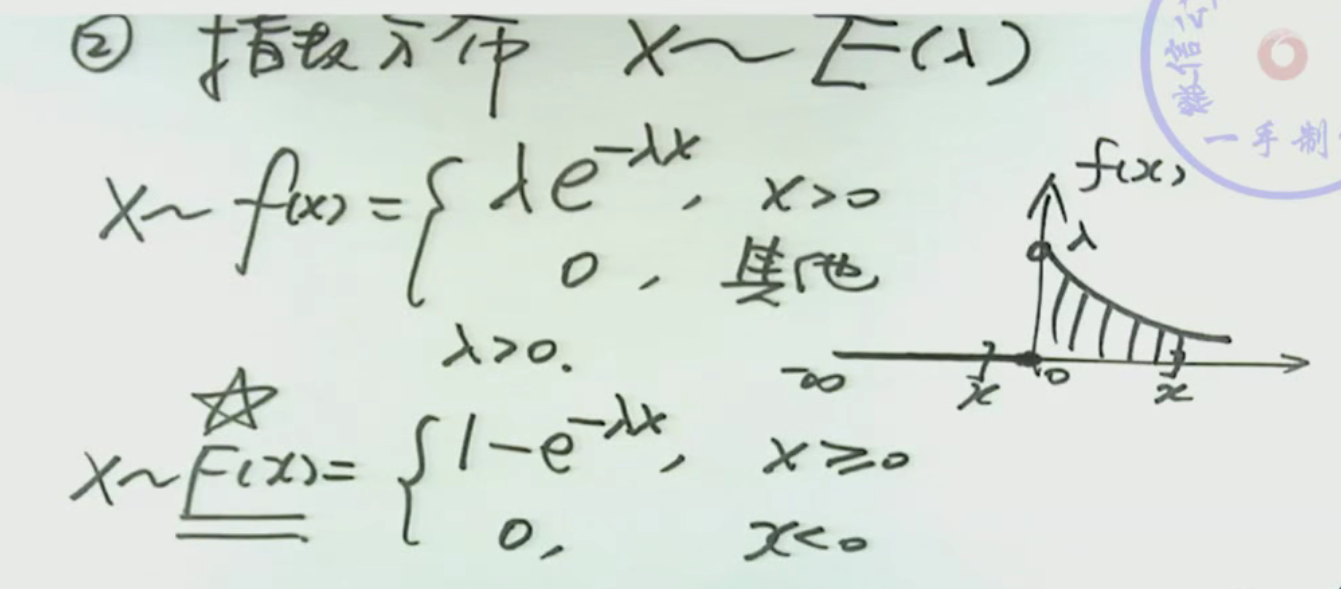
注解:
1.分布函数在x大于等于0的时候的推导:
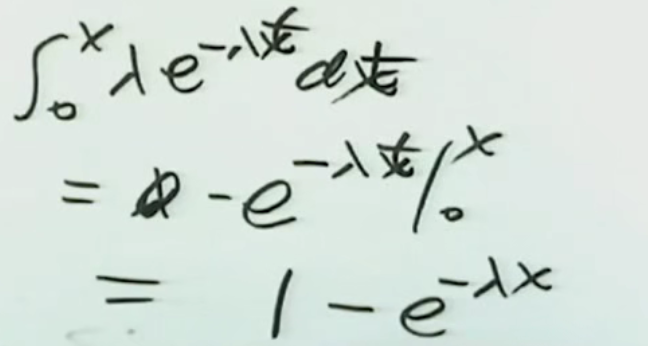
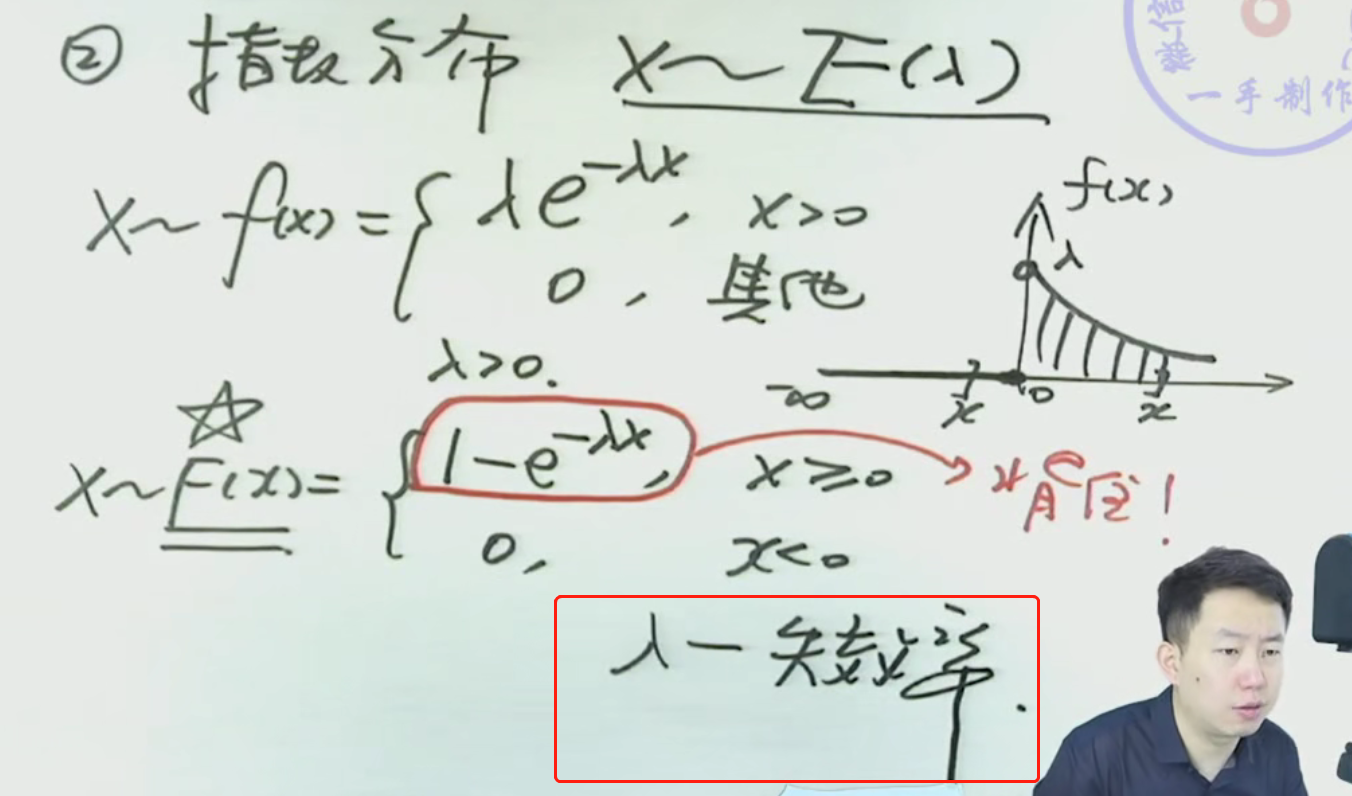
注解:
1.λ是随机变量期望E(X)的倒数。失效率越高,越容易坏掉,平均寿命越短。失效率低,平均寿命高。
2.F(X)的图像:
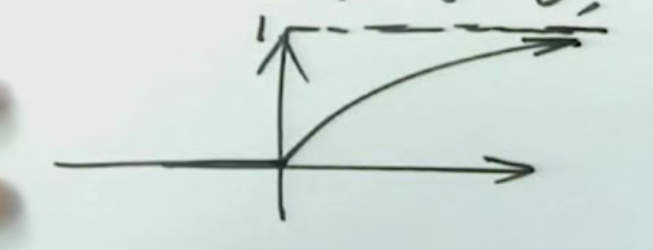
注解:
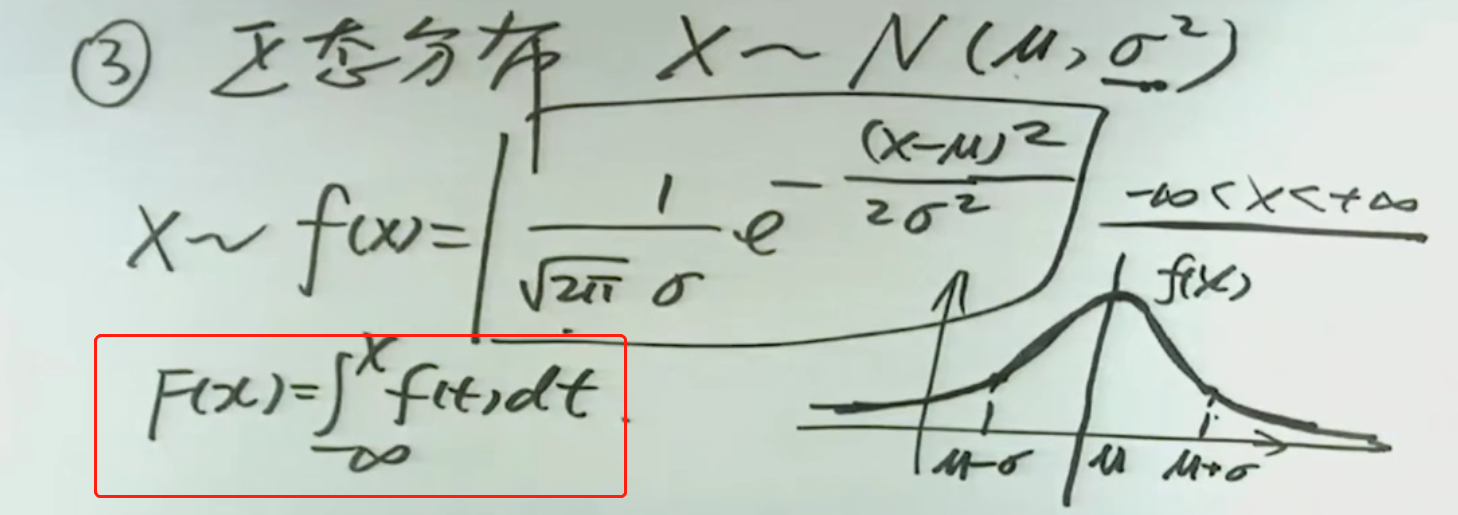
1.X应该被理解为具体发生的事件被映射后的取值,这个取值不是确定的取值,是有一定概率取的值;
2.普天之下,最普遍的概率分布就是正态分布,台湾叫常态分布;
3.中心极限定理会告诉我们,所有分布最后都归结为正态分布;
4.正态分布也叫高斯分布;
5.大样本的情况下,往往都呈现出两头低,中间高的正态分布。
6.μ是数据波动中心,σ是数据波动程度。
7.μ±σ是密度函数凸凹的分界点,是函数拐点。
8.打靶运动员在打出来环数的均值相同的情况下,比较环数数据的波动程度,然后选出来去参加国际比赛。数据上是小波动的更加优秀。
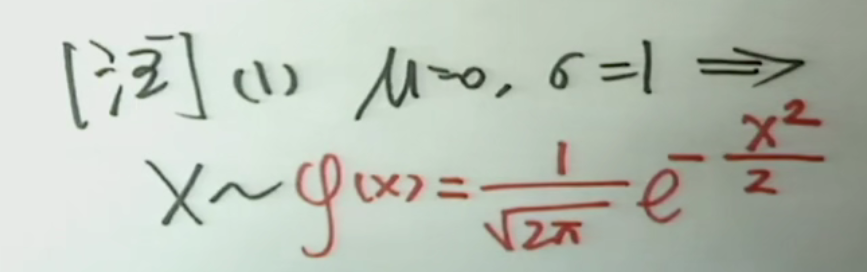
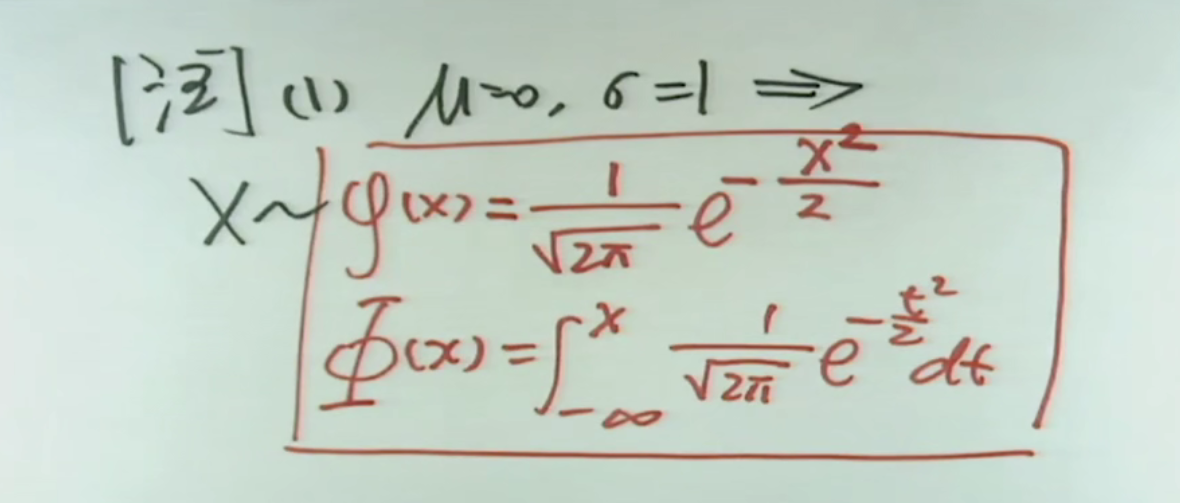
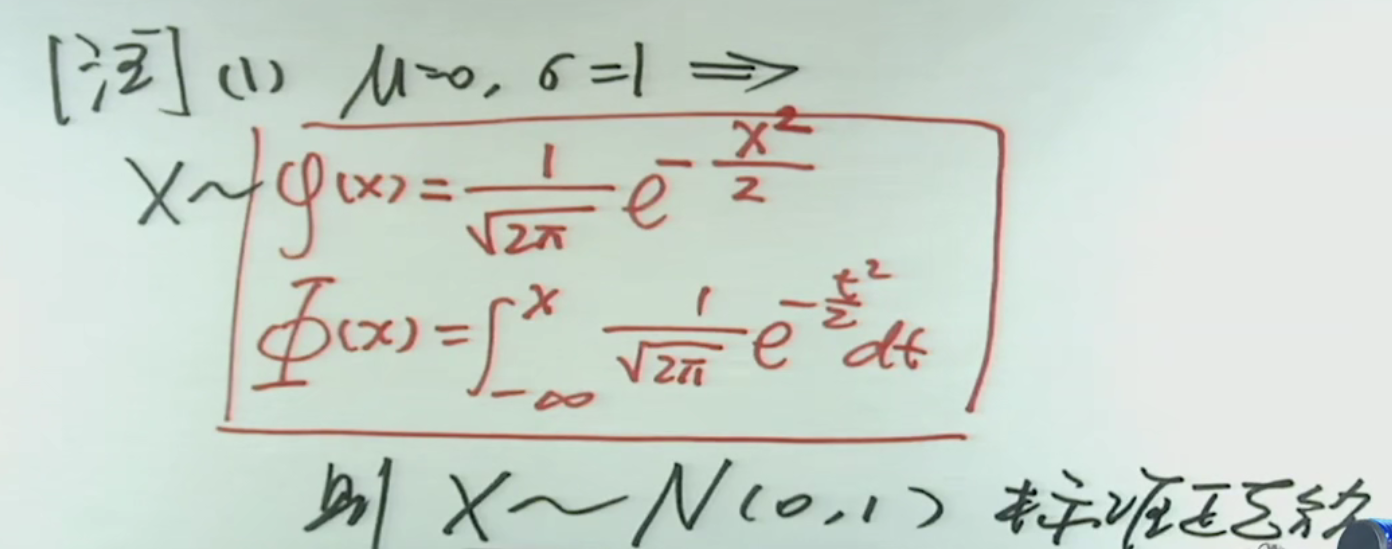
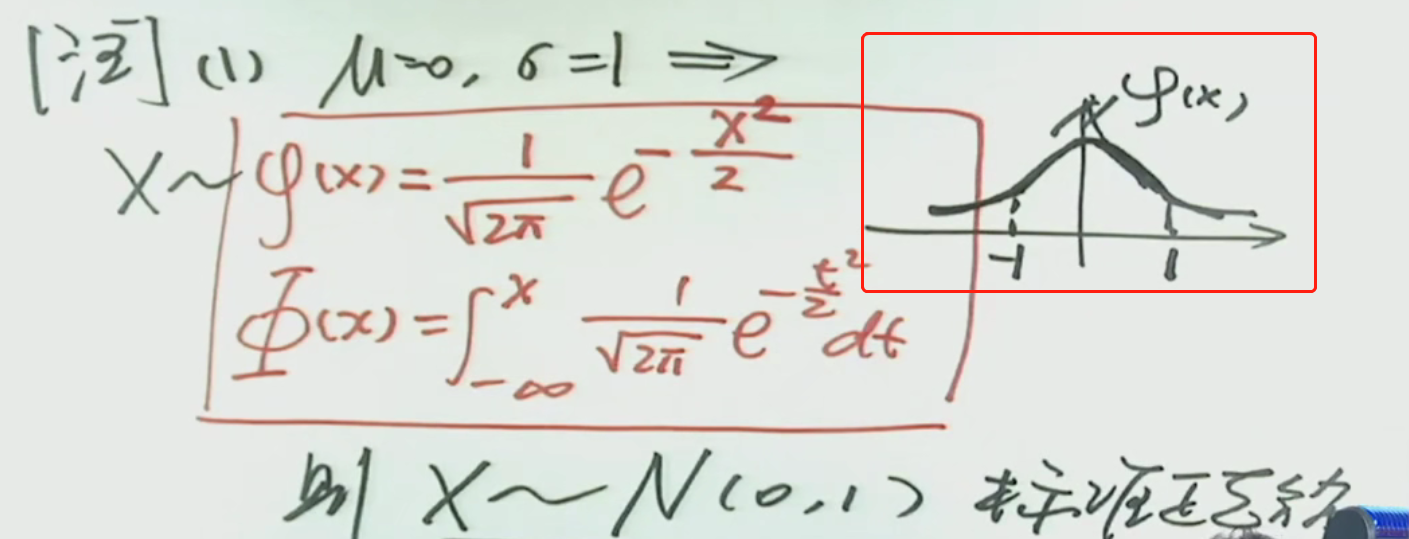
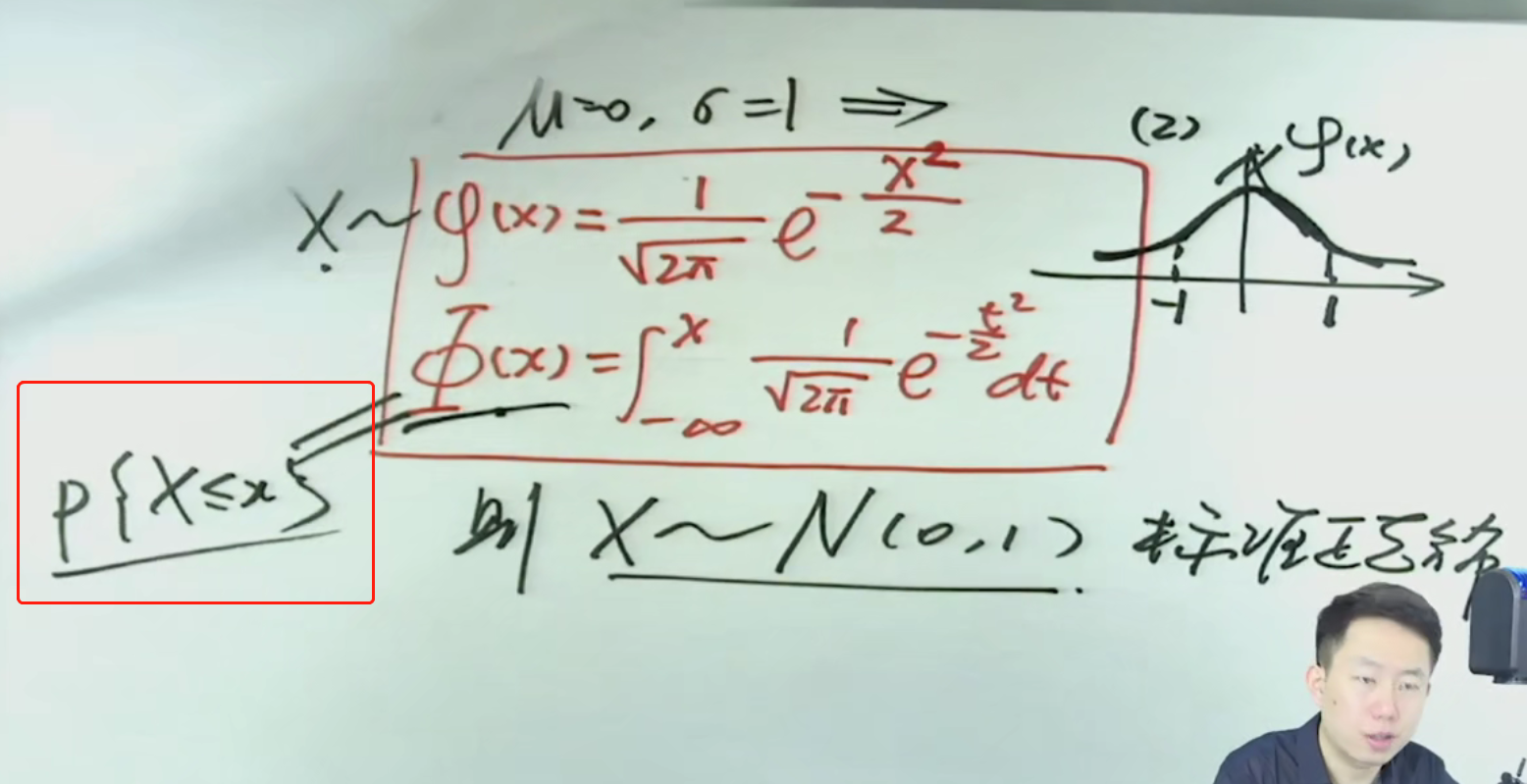
注解:
1.标准正态分布的概率密度函数用小写的φ表示,其它的密度函数都是写成f的。
2.标准正态分布的分布函数用大写的Φ表示,其它的分布函数都是用F表示的。
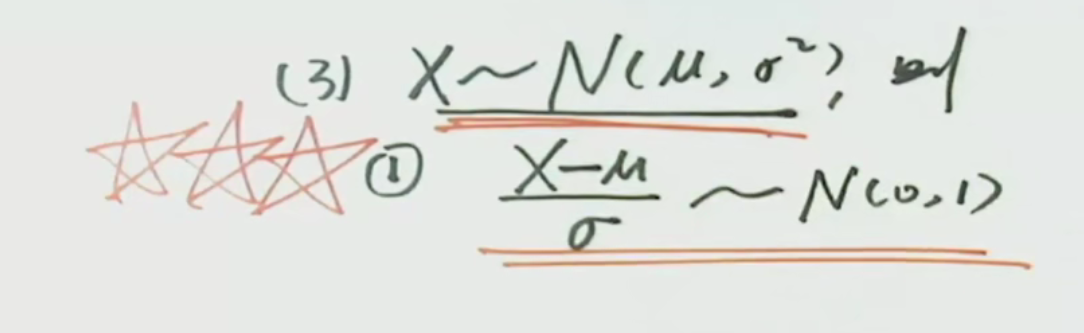
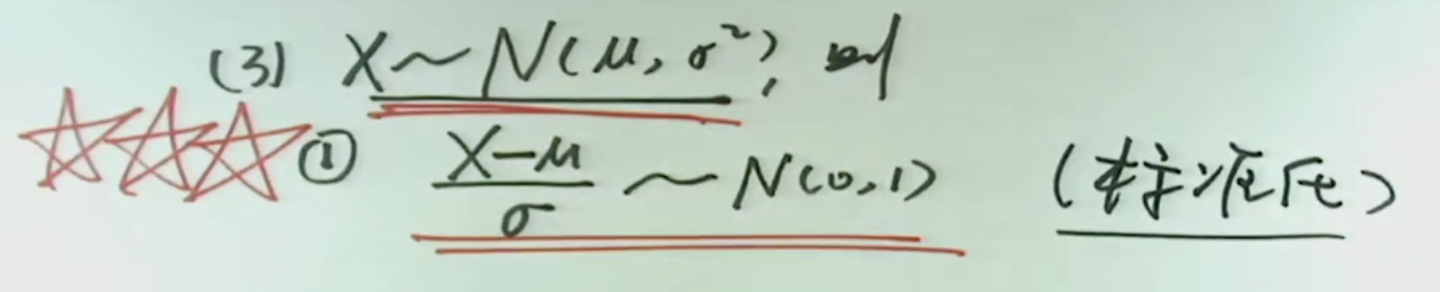
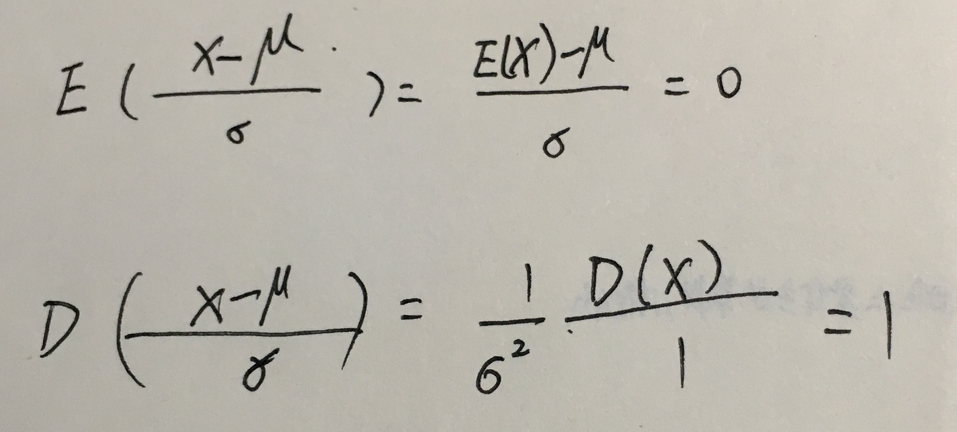

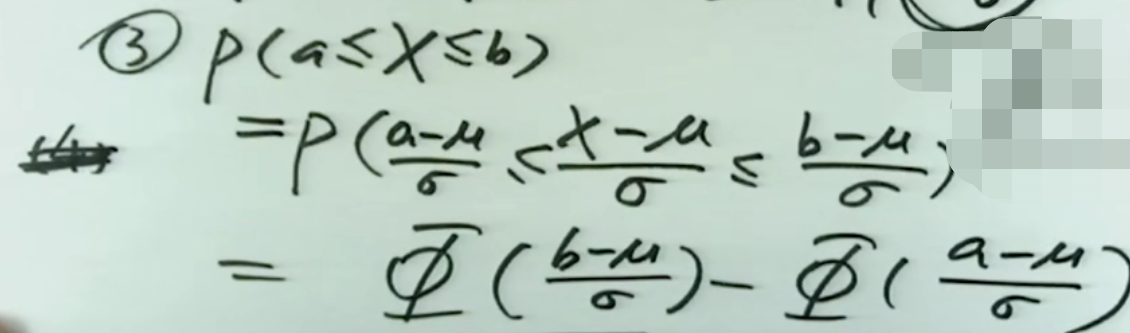
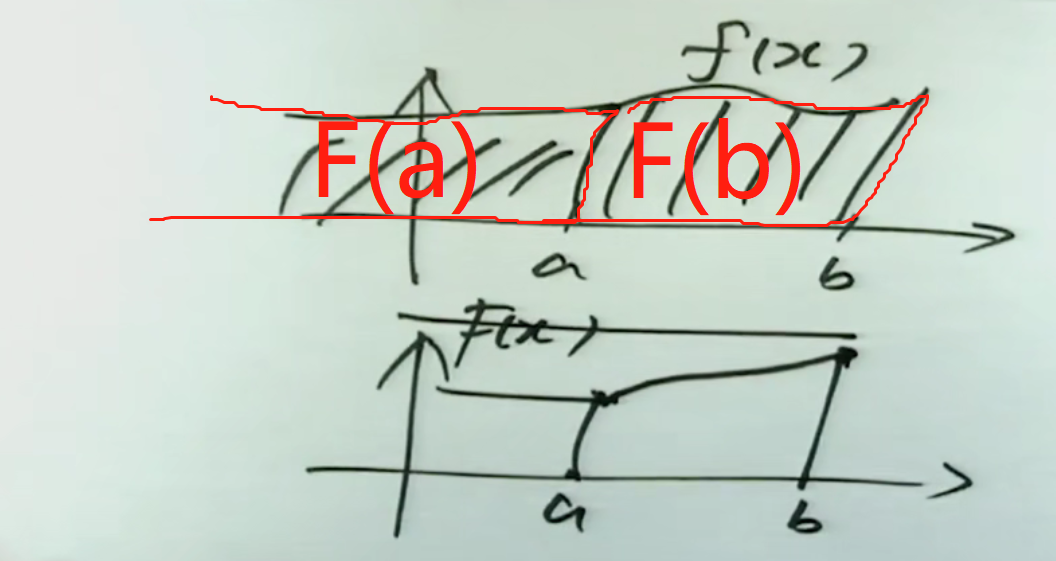
注解:
1.P(b≥X≥a)代表b≥X≥a事件发生的概率。

注解:
1.标准正态分布的概率密度函数是偶函数,所以Φ(-1)=1-Φ(1).
2.这个式子也给出了标准正态分布概率密度函数拐点内的面积值,或者说事件发生在两个拐点之间的概率的大小。
3.看到正态分布首先想到的是标准化。通过正态分布的随机变量的标准化,可以通过查表计算出所有需要求的概率。如Φ(1)的值可以通过查表得到。
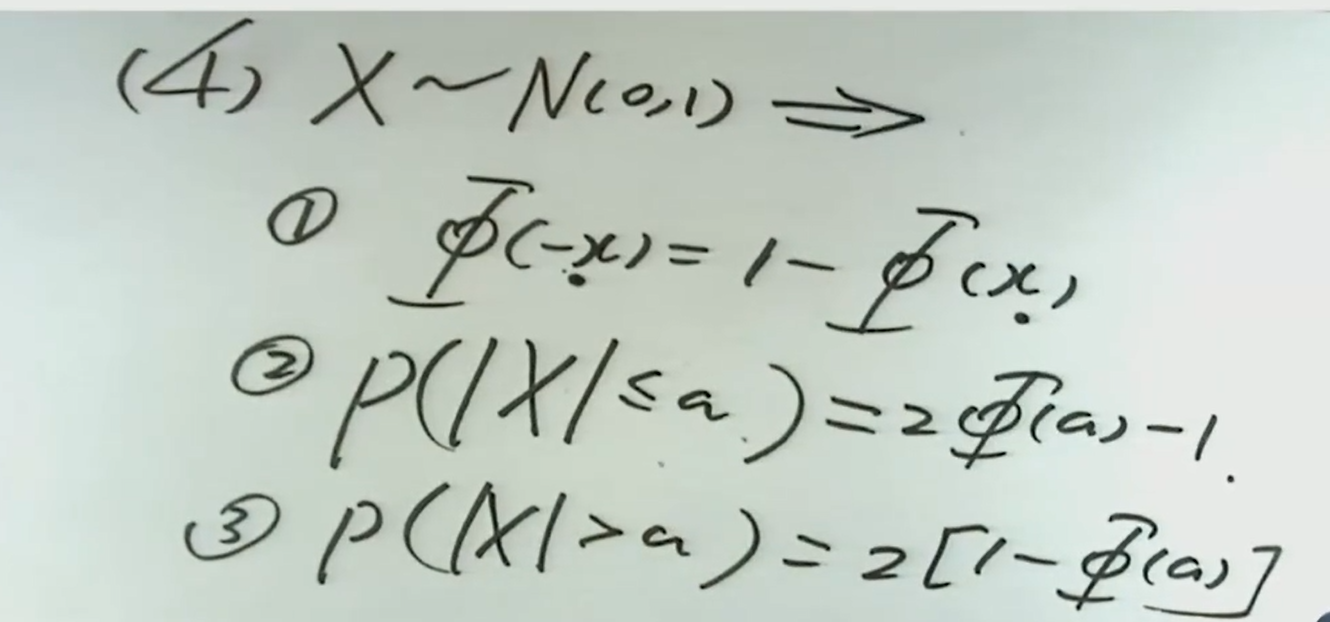
普天之下,最常见的分布有8个:5个离散的(两点或者说0-1,二项,几何,超几何,泊松,)+3个连续型的(均匀,指数,正态)





