神经网络与深度学习-邱锡鹏-学习笔记16-多项式回归
神经网络与深度学习(更新至第6讲 循环神经网络)_哔哩哔哩_bilibili

注解:
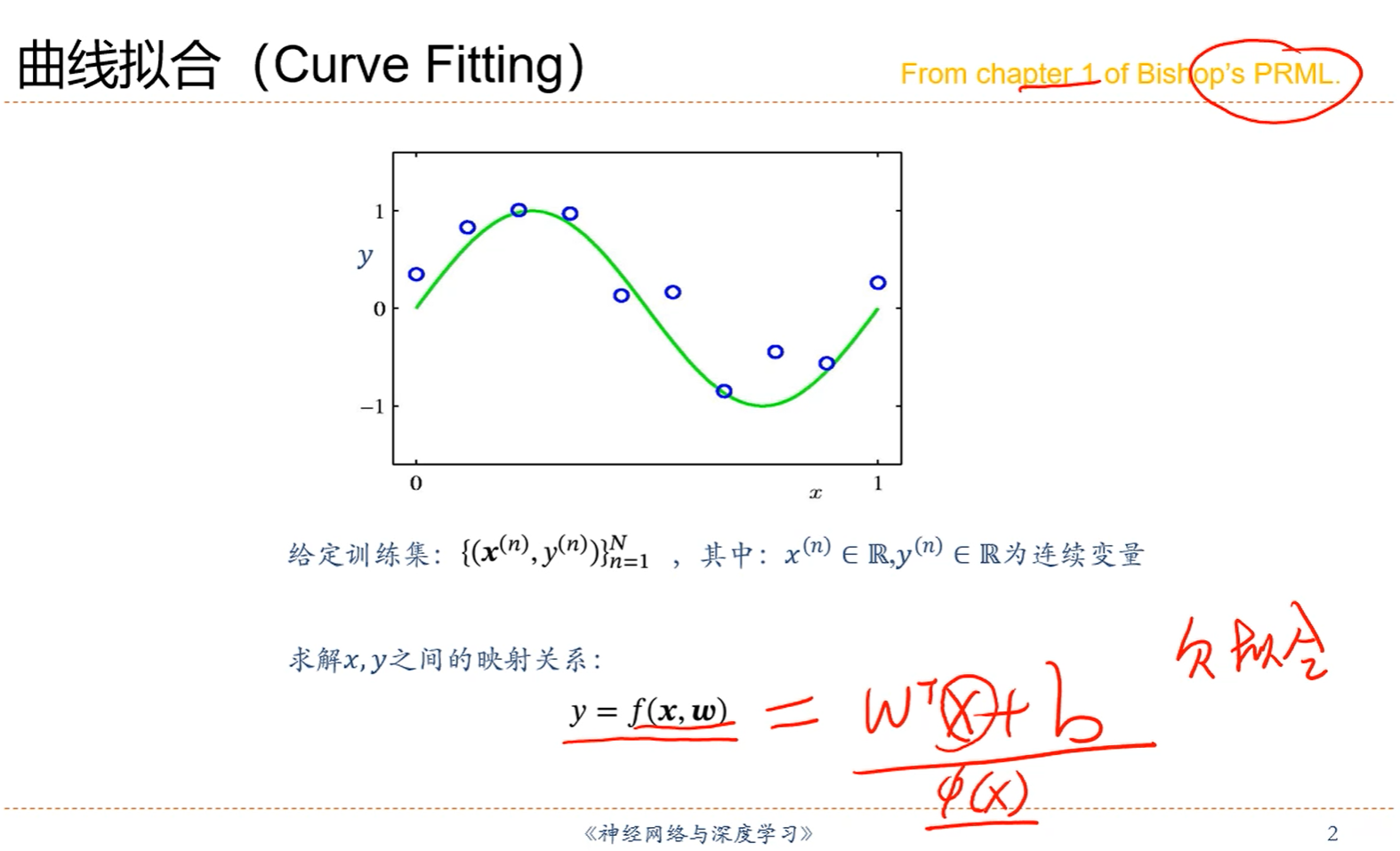
1.非线性的问题假如用线性方程去拟合,那会出现欠拟合的情况。
2.解决办法就是用Ф(X)代替X,如下图:
注解:
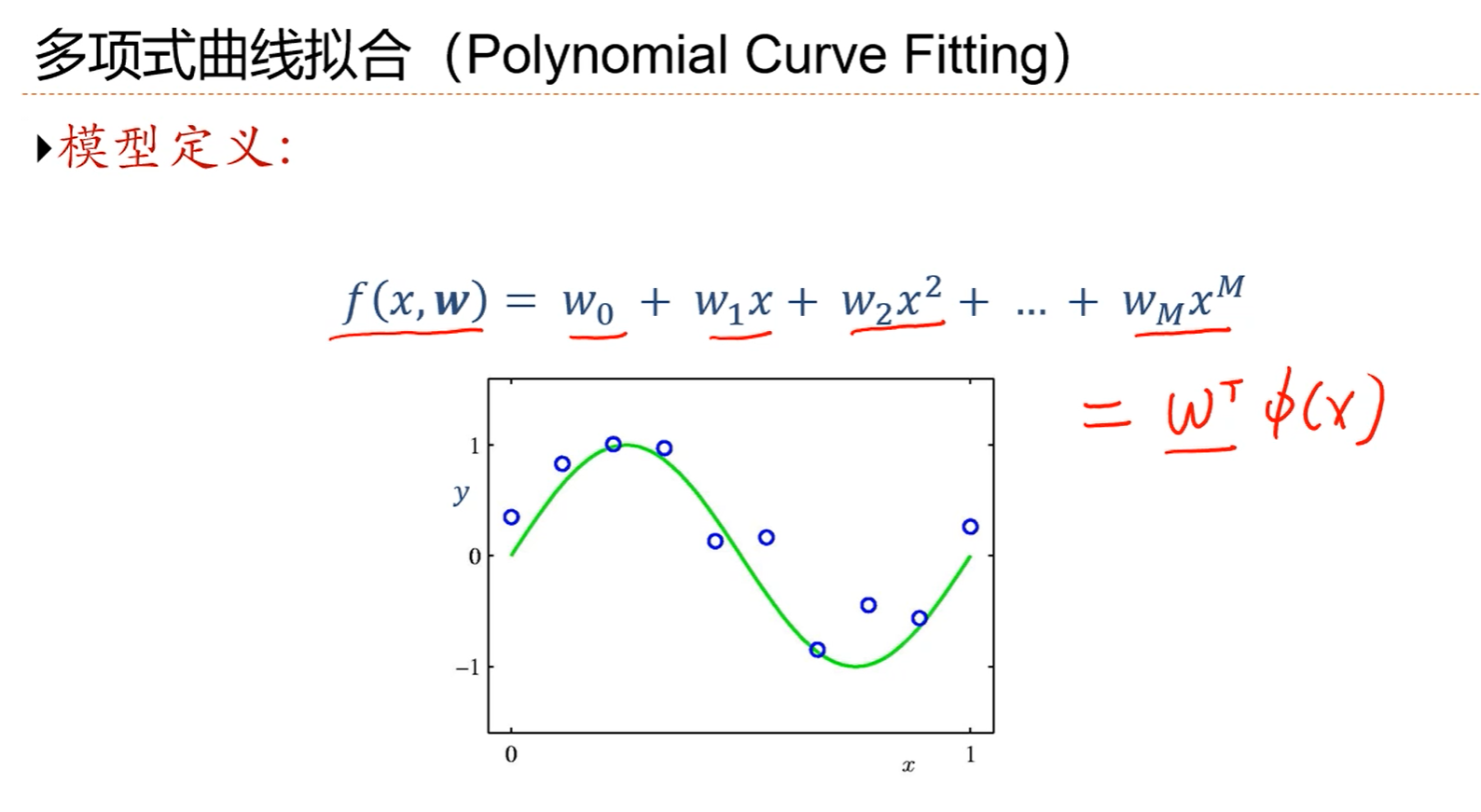
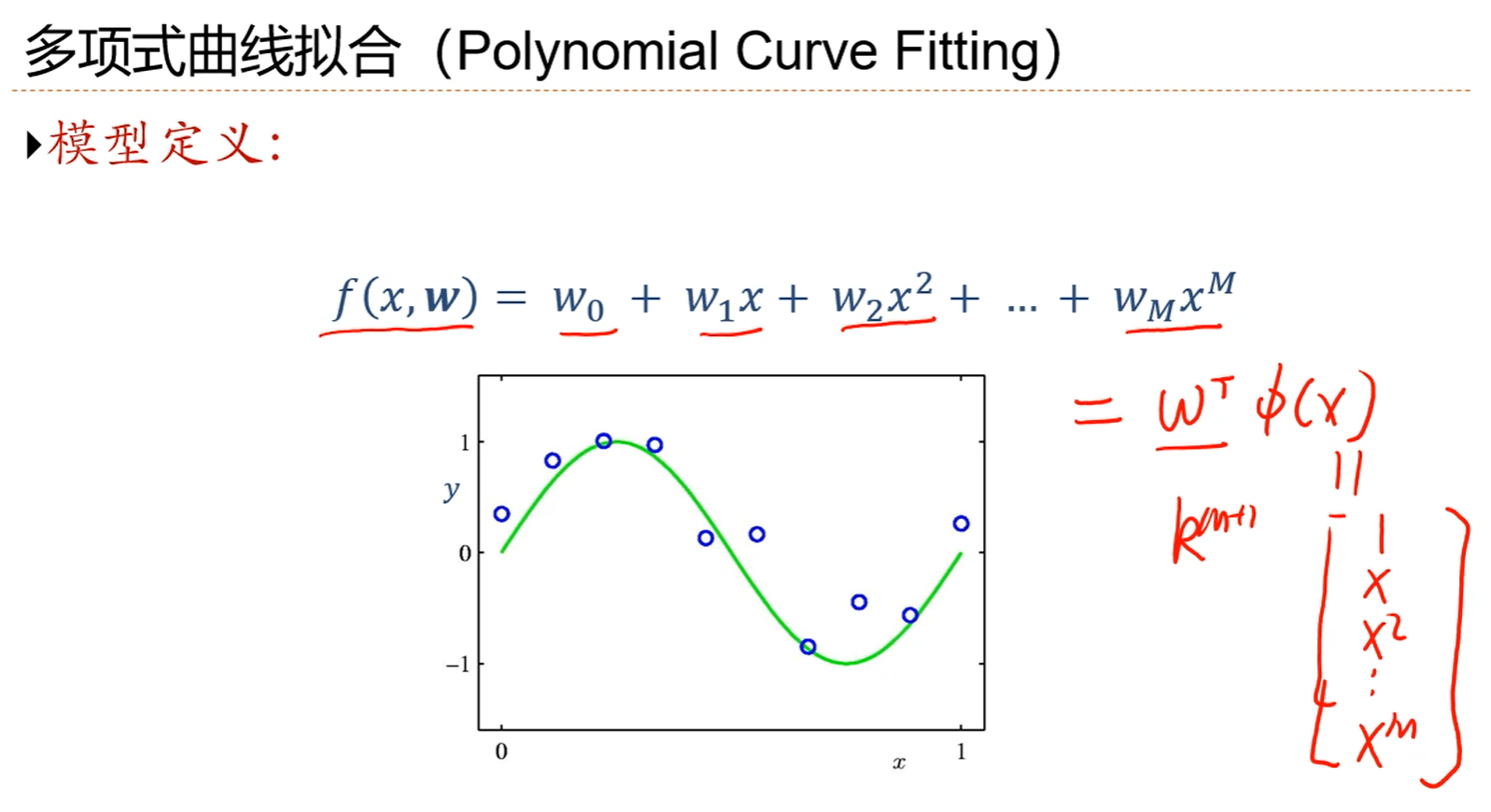
1.依然可以把多项式回归模型写成线性的形式y=wTФ(x),有了这样一个线性形式的话,就可以利用线性回归的最小二乘准则求一个最小二乘解。
2.wT是M+1维度的。
注解:
1.在优化的过程中,模型的次数M并没有当成参数进行优化,所以,M是一个超参数。超参数用来控制函数的形状的。
2.不同的超参数的选择会导致求解出来的权重值w差异很大,那如何选择多项式的次数呢?
3.利用最小二乘准则手工推导权重的最小二乘解。
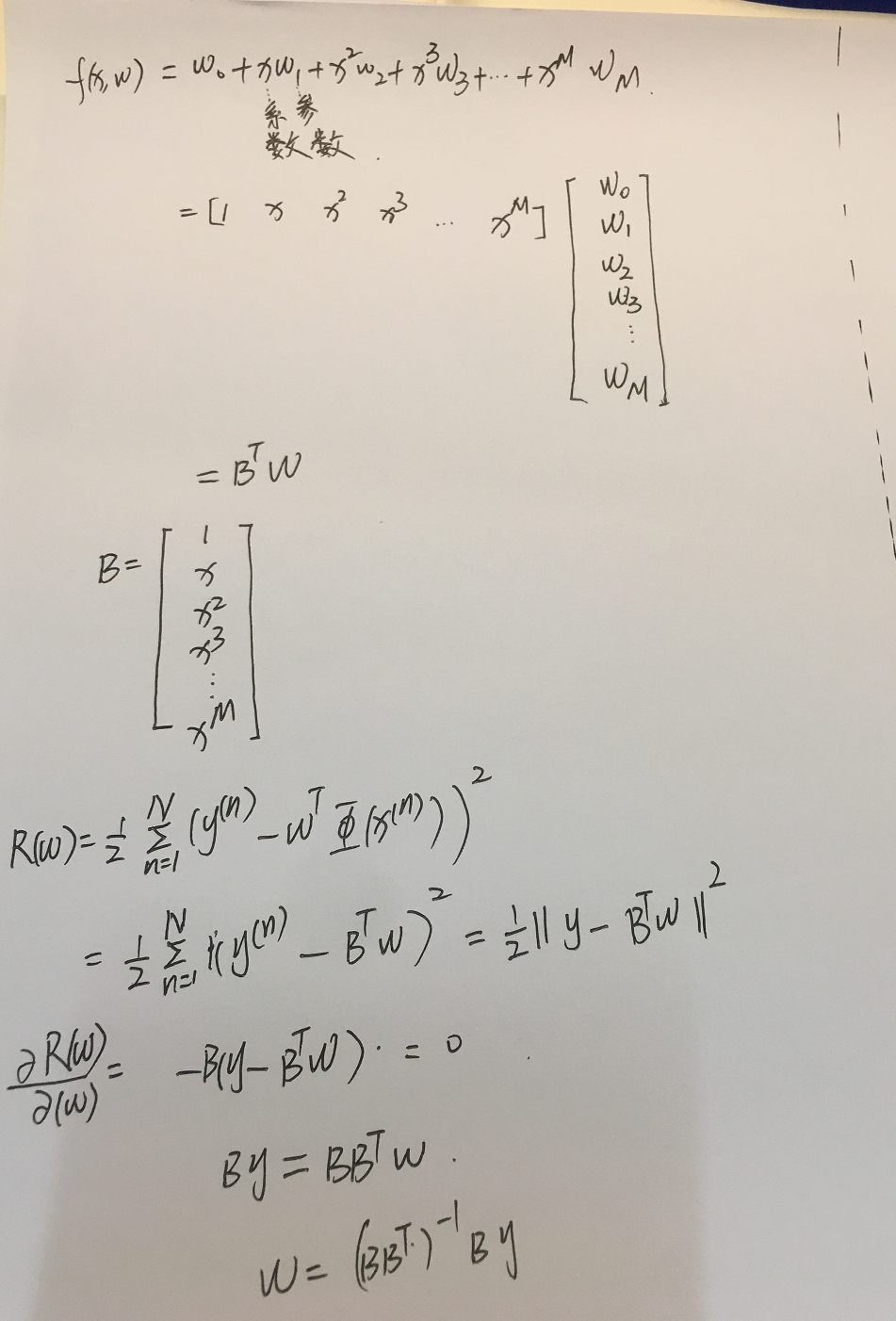

注解:
1.M=0,误差非常大。
2.M=1,比一条横线强一点,但是误差仍然非常的大。
3.M=3,比较符合。
4.M=9,过拟合了,在样本(或者说训练集)上的错误率为0,但是和绿色的真实的线差异很大,加入运用到测试集上,误差一定会很大,因为测试集和训练集是独立同分布的,测试集中的数据一定位于绿色的线附近,此时带入到拟合出来的红色的线里面,误差很大。
5.绿色的线是真实的线。
6.到底M,也就是多项式的次数选择多少合适呢?这就是一个模型选择的问题,这是一个很难的问题。
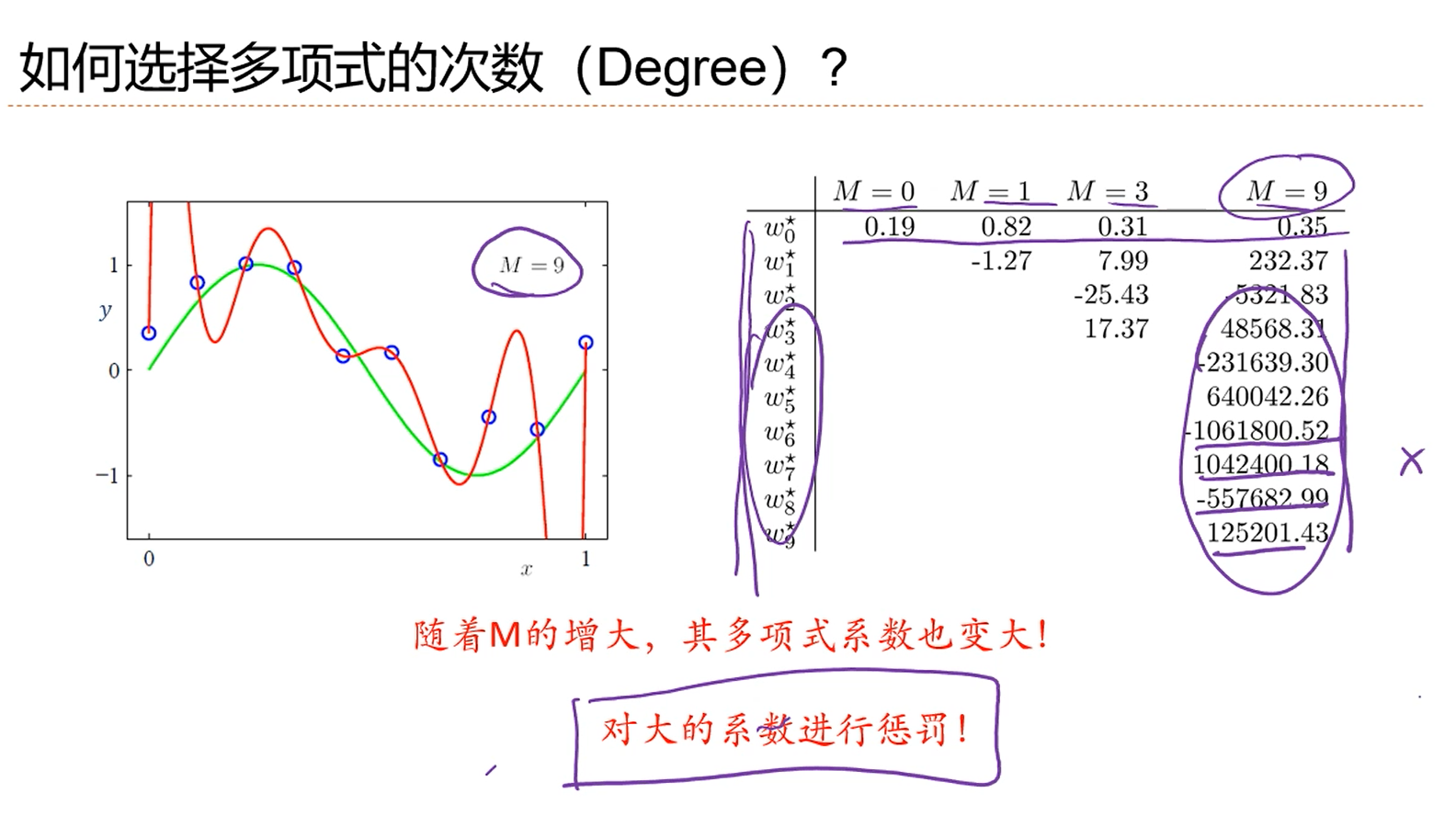
注解:
1.这个拟合问题是x∈(0,1)之间的数,当拟合的次数M=9时候,第一个系数的量级还能和前面的拟合模型还能保持一致,但是后面的自变量(特征)的高次幂的系数非常的大,这是因为1>x>0,高次幂自变量的权重系数必须很大才能匹配当前的y值。y的范围看图应该是[-1,1].这些大的系数,会带来一个问题就是。模型非常的不稳定。不稳定的地方表现在:稍微变动一个x值,所求出的权重系数就会发生很大的变化。或者说,x的一个很小的扰动,会造成权重的一个很大的变动。所以说,求出来的权重很不稳定。或者说,用一批样本点求出的系数和用另一批样本点求出的系数会有很大的差异,这不是我们所希望的结果。此时,属于过拟合,这样的情况下,用异于拟合点的新的样本点带入到拟合模型,误差会很大很大。这个时候,怎么办呢?对大的系数进行惩罚,限制高次幂权重系数的量级。惩罚的方法是:在原有的损失函数(目标函数)的基础上,引入正则化项。
2.x的一个很小的扰动,会造成权重的一个很大的变动:
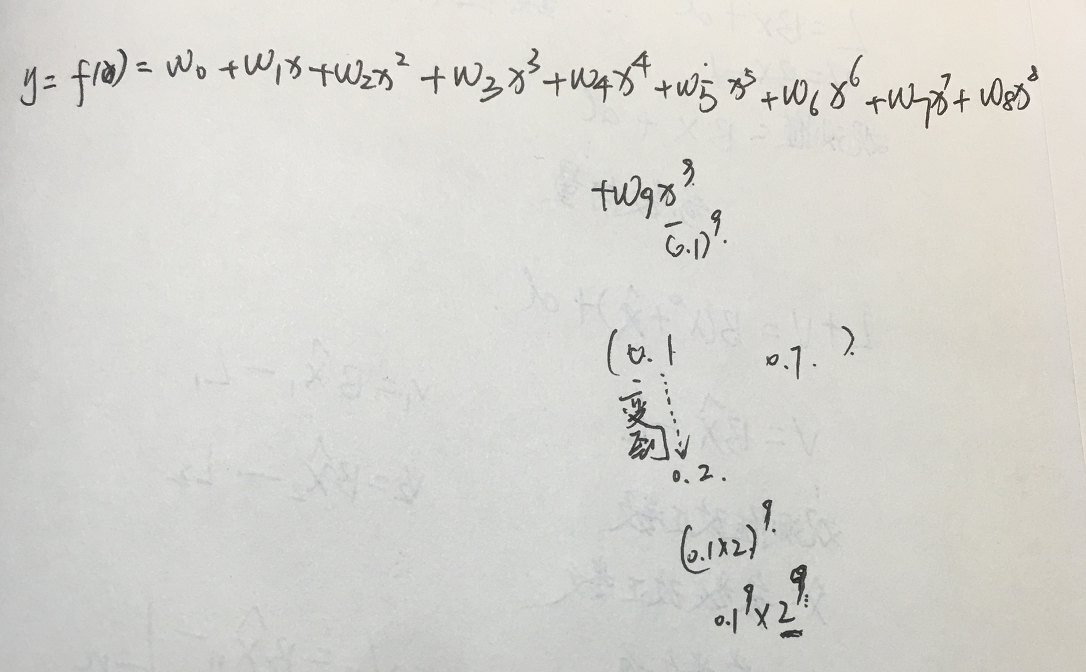

注解:
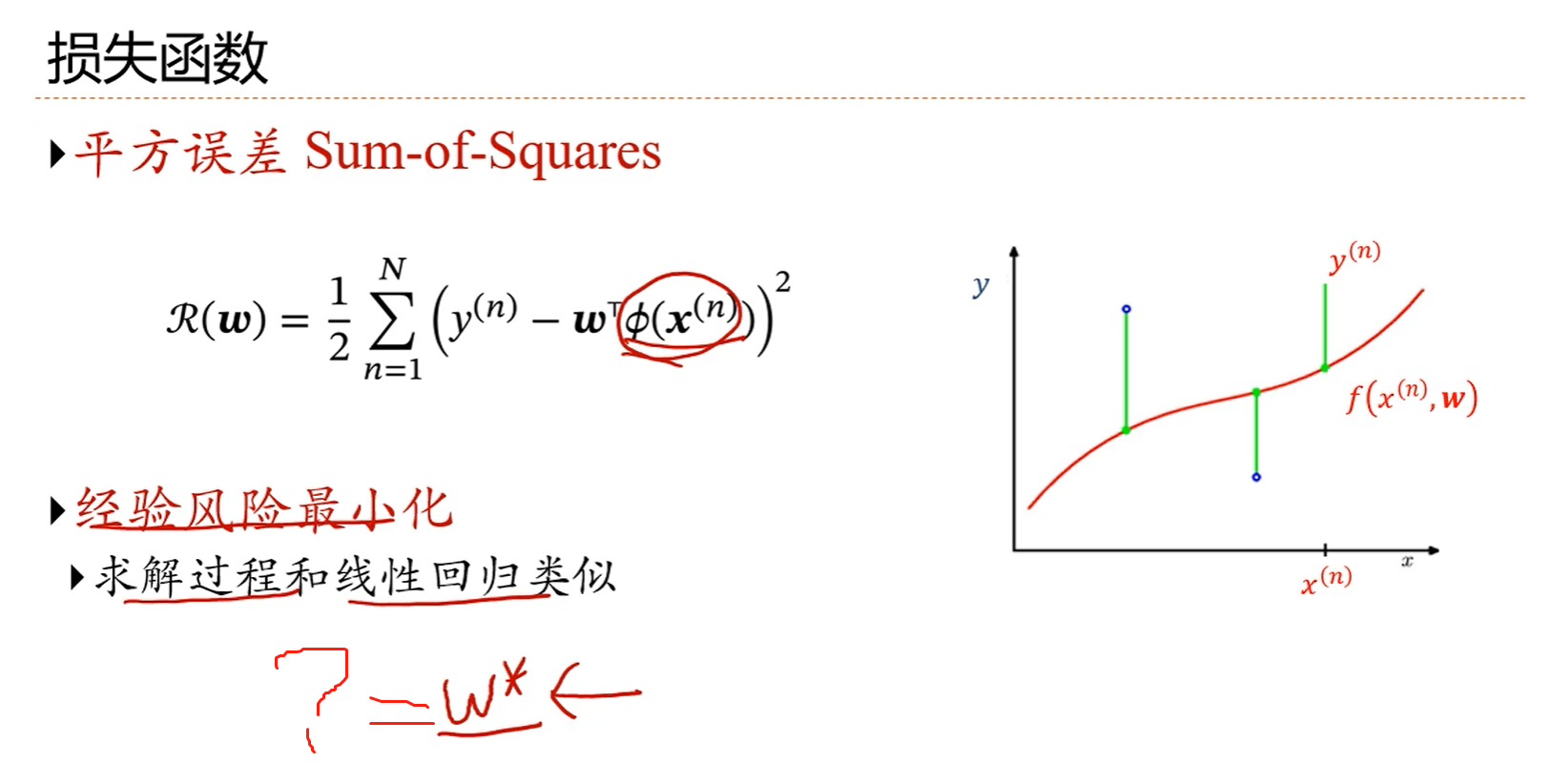
1.若要使得等式左边的R(w)最小,既要等式右边的第一项最小,也要等式右边的第二项最小。
2.若要使得等式左边的R(w)很小,w的值就不能很大。
3.手动推导w*?


注解:
1.λ取e-∞的时候,λ此时接近0,几乎相当于么有约束,此时模型还是过拟合。
2.在λ取e-18的时候,虽然说模型次数M=9,但是拟合的还算不错。权重系数被限制在了一定的范围内了。
3.λ取1的时候,限制的强度更大,模型已经退化成了直线了。
4.λ也是属于一个超参数,因为是人工定制的。人工输入的。它在神经网络中非常关键,它的取值会影响模型的好坏。
5.λ取值的不同,意味着神经网络拟合的是不同的模型。这就是深度学习网络模型在训练的时候需要验证集的原因,因为不同的模型需要在验证集上验证模型误差(残差)的大小。

注解:
1.控制过拟合的另一个办法是:增加训练样本数量。
2.图中是模型次数M=9的情况。
3.当拟合样本量N非常大的时候,经验风险就趋近于期望风险。就是说残差会趋近于真实模型的残差。
本节小结:讲了非线性拟合的情况,也就是高次幂拟合的情况,其实深度学习的神经网络拟合大部分应该是属于非线性拟合的。只是非线性拟合的次数很难确定,如果过小,会欠拟合,过大,会过拟合。一般的话,神经网络的拟合,模型次数应该不会很小,这时候出现过拟合就避免不了,再过拟合的时候,权重系数可能会很大。那如何避免过拟合呢?就是再待优化函数的后面加上一个惩罚项,也叫正则项,这个正则项限制了过大的权重系数的出现。使得虽然模型次数定的很高的时候,也能得到一个较为理想的拟合结果。
另一个避免模型次数高的情况下出现过拟合的办法就是增加训练样本的数量,此时残差会趋近于真实模型的残差,虽然说真实模型永远不可能知道。

