阿贝尔定理

“还我2块钱” 张宇老师爆笑故事+直播事故！_哔哩哔哩_bilibili

 

阿贝尔深入研究了椭圆积分的问题.

1637年，费马去图书馆看书，违反规定，在图书上乱写，写出了费马大定理。

356年后的1993年，费马大定理被美国数学家安德鲁.怀尔斯解决，他使用的核心方法就是椭圆积分。

 

假如生活在19世纪的阿贝尔没有死去，费马大定理可能轮不到20世纪的人解决。

阿贝尔得了肺结核无钱医治死去。

数学上，高斯排名第一，牛顿第二。但阿尔巴的天分应在高斯之上，后者可能感觉到了威胁，所以打算不资助他。后者看了前者的论文只是说：我看不懂，可能没有什么价值。

阿贝尔定理：

 

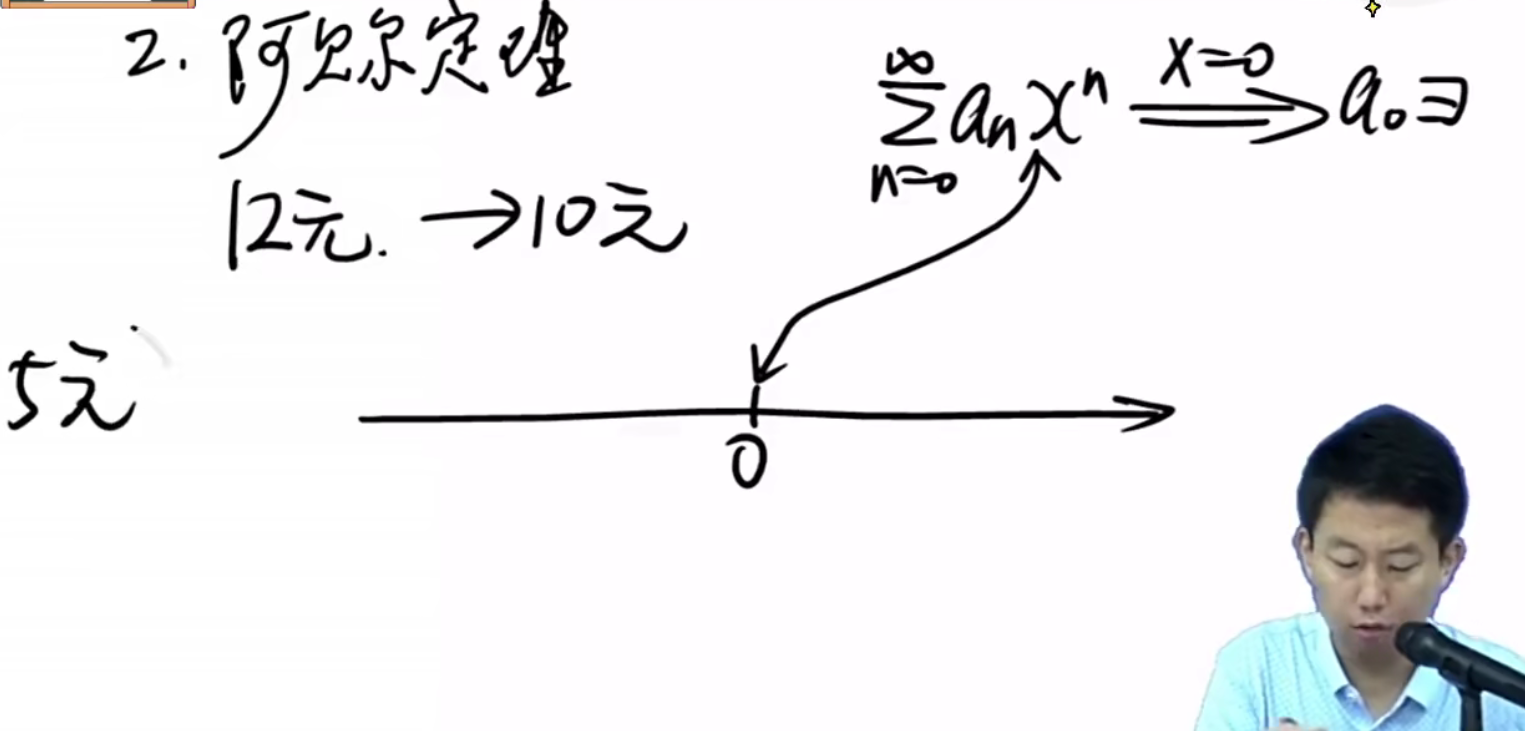
已知：上面的级数在x=0这一点一定是收敛的，因为在x=0这一点有确定的数值a₀.

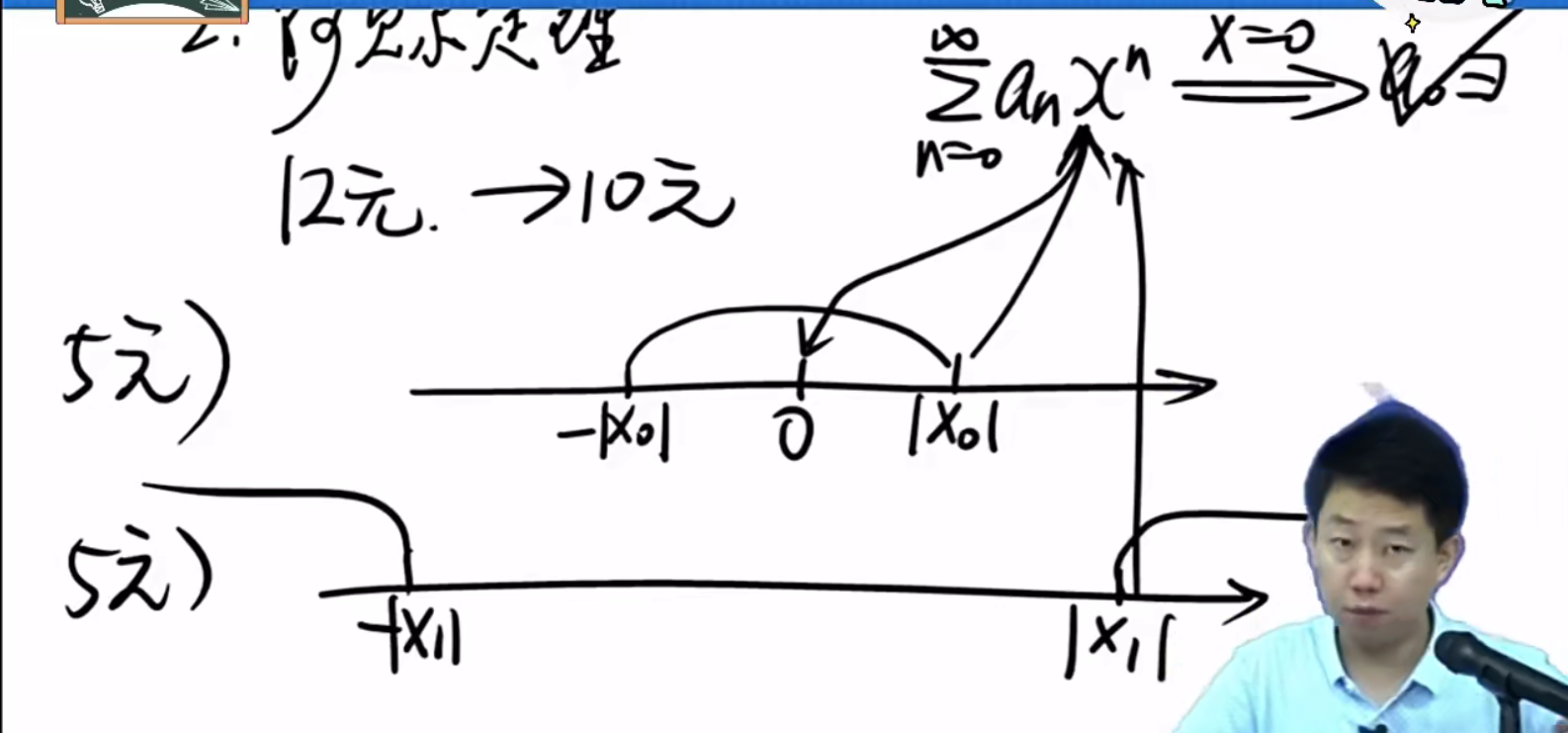
阿贝尔：假如还能找到一个异于x=0的点，使得级数的值存在，即使得级数收敛，那么，在（-|x₀|,|x₀|）区间，级数必定处处绝对收敛。假如能找到一个异于x=0的点x1，带入级数后，级数是发散的，那么级数在(-∞,|x₁|)及(|x₁|,+∞)区间上发散。

 

 

 

 

 

 

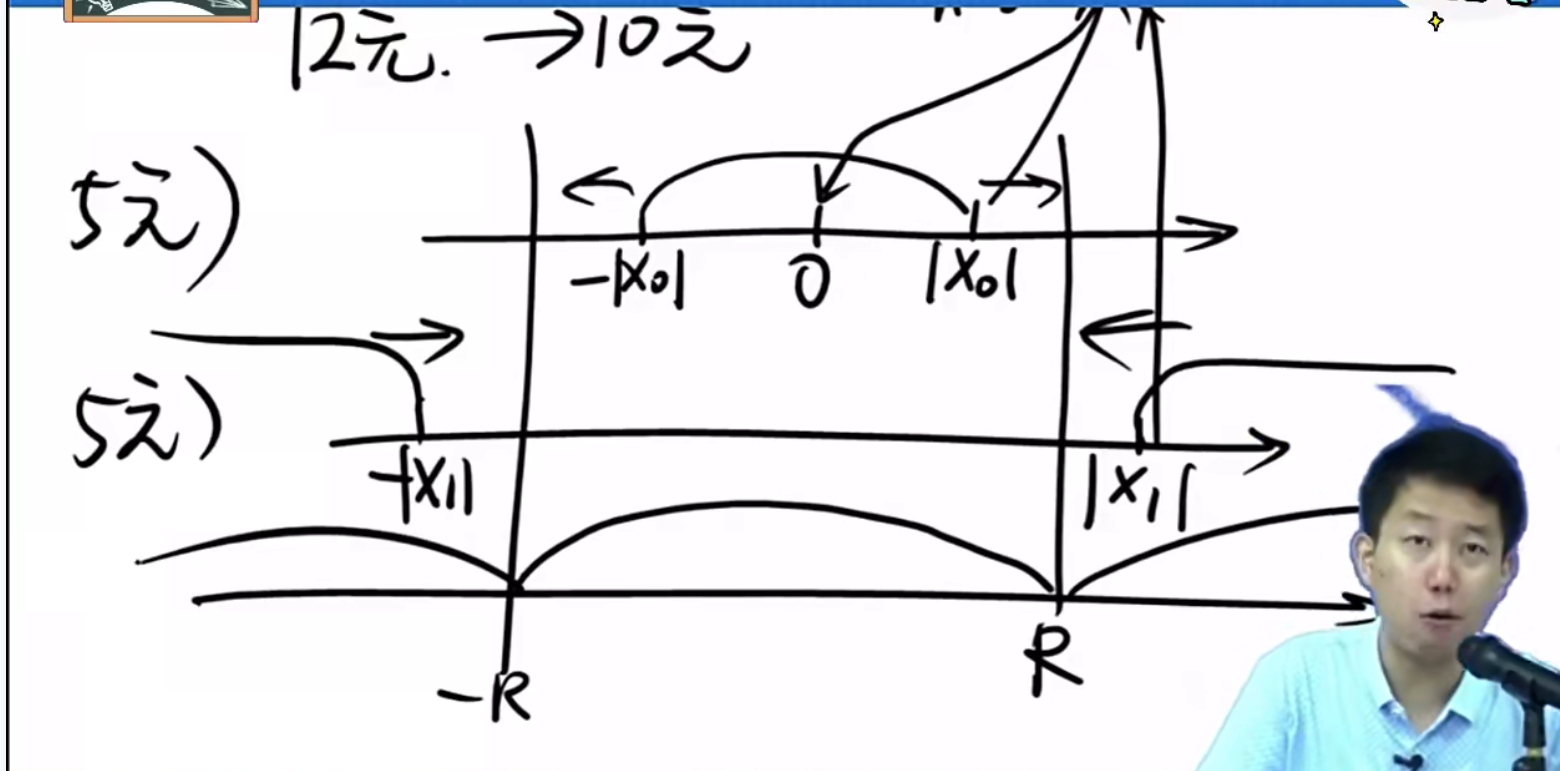
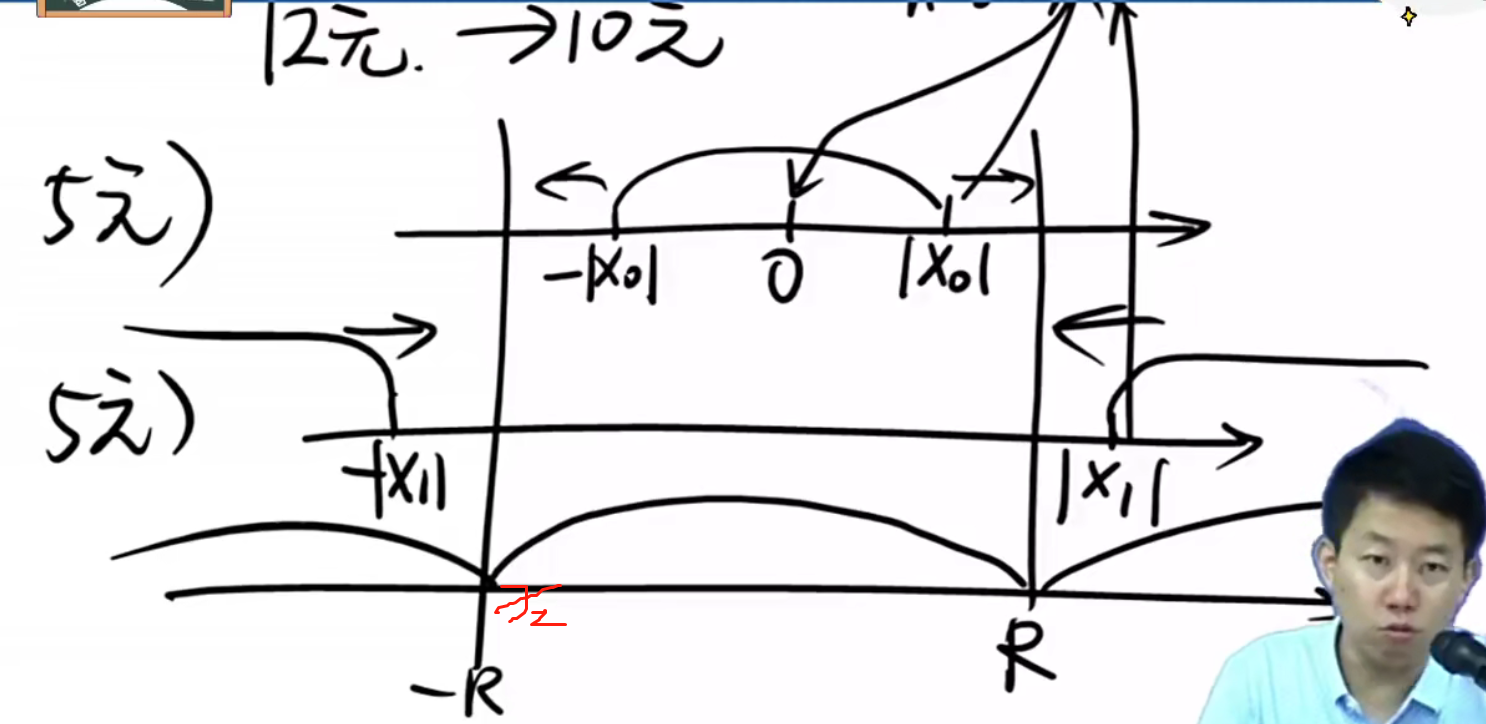
注：

1.当收敛区间扩大和发散区间也叩打的时候，它们一定会相遇在某一点x₂，在这一点处，(-R,+R)区间级数处处绝对收敛，这个区间外发散。

2.在x₂那一点处，级数是收敛还是发散呢？阿贝尔没有说。达朗贝尔，柯西在这一点都不讲话的。只有一个办法：把-R和+R那两个点带入到级数里面再作判断（讨论），很麻烦的。