P6列空间和零空间

https://www.bilibili.com/video/BV1zx411g7gq?p=6

P并L不是R³的子空间的原因：P中的一个向量和L中一个向量相加，其结果不属于P，也不属于L，所以不在P并L的集合里面。可见对加法不封闭，所以不是一个空间，自然也不是一个子空间。

S和T都属于某个空间R³的子空间，则它们的交集也属于R³的子空间。证明：

它们属于交集，它们即属于S，又属于T，

答案是：属于。

v和w都属于S，而S是子空间，即S是一个空间于S。它们对于T也如此。

所谓向量空间，

如果加法封闭，数乘封闭，那么线性组合必然也封闭。

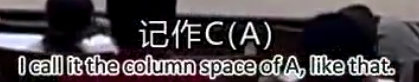
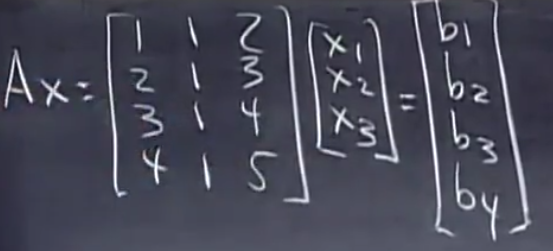
本例的零空间是：

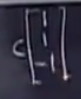
包含原点，向两端无限延伸。

心得体会：

对于线性方程组，矩阵可以看成是由各个列向量线性组合成的列空间，解是另一个子空间。

补充的知识点：

线性代数中一些等价的结论

http://zhuanlan.zhihu.com/p/336413608

$\mathbf{A}\in \mathbb{R}^{n \times n}$

$\mathbf{A}$ 是非奇异的：

$\mathbf{A}$ 是可逆的
$\mathbf{A}$ 的列向量是线性无关的
$\mathbf{A}$ 的行向量是线性无关的
$\mathbf{A}$ 的行列式是非零的
$\mathbf{Ax=0}$ 有唯一解
$\mathbf{Ax=b}$ 有唯一解 $\mathbf{x = A}^{-1}\mathbf{b}$
$\text{rank}(\mathbf{A}) = n$
$\mathbf{A}$ 有 $n$ 个非零的pivot
$\mathbf{A}$ 经过初等行变换和列变换可以化简为 $\mathbf{I}$
$\mathcal{C}(\mathbf{A}) = \mathbb{R}^n$
$\mathcal{C}(\mathbf{A}^T) = \mathbb{R}^n$
$\mathbf{A}$ 所有的特征值非零
$\mathbf{A^TA}$ 是对称正定矩阵
$\mathbf{A}$ 有 $n$ 个正的奇异值

注： $\mathcal{C}(\mathbf{A})$ 是指 $\mathbf{A}$ 的列空间（Column Space）, $\mathcal{C}(\mathbf{A}^T)$ 是指 $\mathbf{A}$ 的行空间（Row Space）

反之，我们可以得到

$\mathbf{A}$ 是奇异的：

$\mathbf{A}$ 是不可逆的
$\mathbf{A}$ 的列向量是线性相关的
$\mathbf{A}$ 的行向量是线性相关的
$\mathbf{A}$ 的行列式是0
$\mathbf{Ax=0}$ 有无穷多个解
$\mathbf{Ax=b}$ 无解或有无穷多个解
$\text{rank}(\mathbf{A}) < n$
$\mathbf{A}$ 有 $r < n$ 个pivot
$\mathbf{A}$ 经过初等行变换和列变换可以化简为 $\mathbf{R}$ , $\mathbf{R}$ 至少有一个行向量是 $\mathbf{0}$
$\text{dim}(\mathcal{C}(\mathbf{A})) < n$
$\text{dim}(\mathcal{C}(\mathbf{A}^T)) < n$
0是 $\mathbf{A}$ 的特征值
$\mathbf{A^TA}$ 是半正定矩阵
$\mathbf{A}$ 有 $r < n$ 个正的奇异值

作者：ACoder
链接：https://zhuanlan.zhihu.com/p/336413608
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

posted on 2021-03-01 19:00 一杯明月阅读(323) 评论(0) 编辑收藏举报

刷新页面返回顶部