P2 矩阵消元

https://www.bilibili.com/video/BV1AC4y187WN?p=3

可以参考的资料：http://max.book118.com/html/2019/0312/5103111210002020.shtm

要点：

1. 消元法求解任意元的线性方程组。
2. 多少元就是多少种线性组合的意思。
3. 整个课程的核心概念是“矩阵变换”。

 

 来源：https://max.book118.com/html/2019/0312/5103111210002020.shtm

对于消元法：

 

 消元法和矩阵运算是联系在一起的。

x+2y+z=2
3x+8y+z=12
      4y+z=2

 用矩阵表示是：

AX=b

  

 

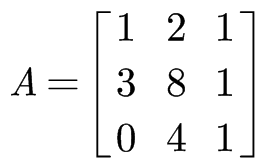
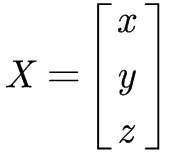
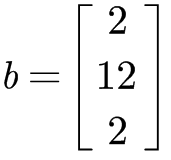
 对方程组实施消元法实际上是对矩阵A进行初等行变换。

在消元的时候，用矩阵来做看上去会更加的简洁。

 

 

最后加上增广矩阵后，消元的结果是下面这个矩阵。

 

 

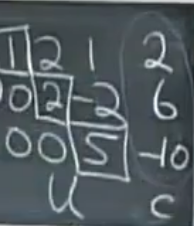
 这个是增广矩阵。c是b化来的，就像U是A化来的一样。

 

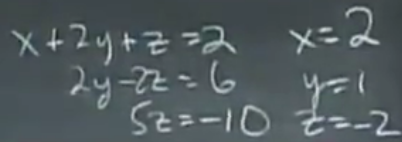
 这个步骤叫做回代，回代后就能解出未知数的值。

 

 

 

 

 什么矩阵能达到消元（消掉x）的目的？

 

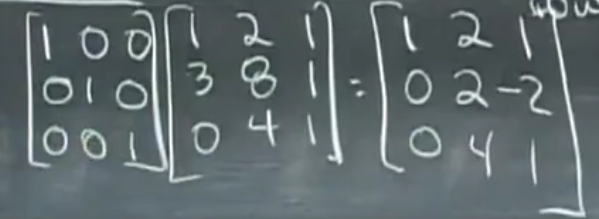
 左边这个叫做单位矩阵。

 

 

 

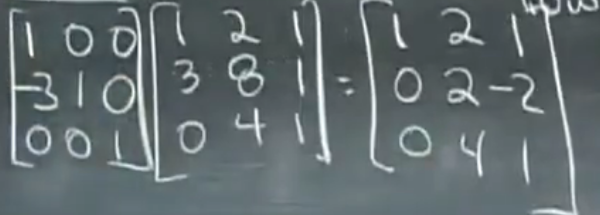
 乘上左边的矩阵就行了，左边的这个矩阵叫做初等矩阵（单位阵经过一次初等变换得到的矩阵 ）。

 

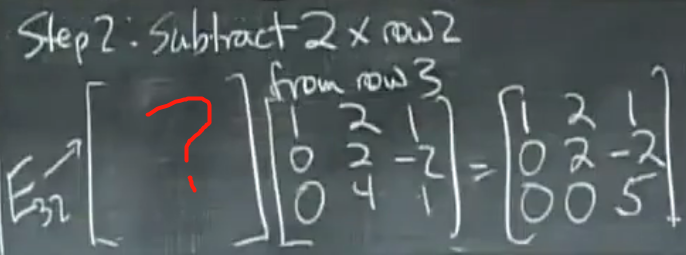
  什么矩阵能达到消元（消掉y）的目的？

 

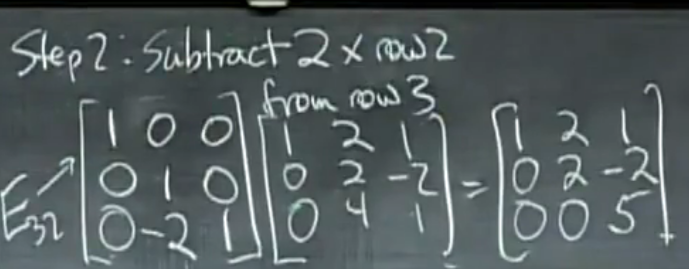
 消元至此结束。每一步都用到了一个初等矩阵。

综合第1步和第2步考虑：

 

 

 

 

 

 

 

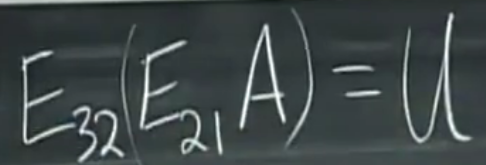
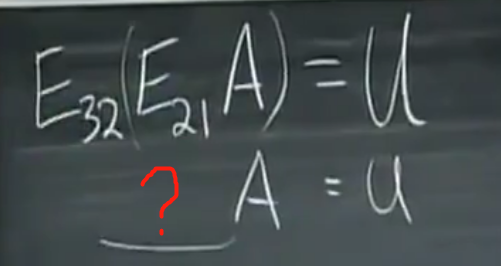
 这就是矩阵乘法的结合律。

 

 

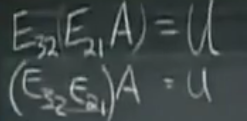
 第1个矩阵的行变换是怎么来的？

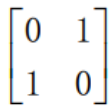可以看成是先取右边矩阵的2行，再取右边矩阵的第1行。这样就完成了对矩阵的行的置换。

 

 列置换在解方程的矩阵消元中用不到。后者只用到了行变换。

矩阵要进行行交换，就在矩阵的左边乘上某个矩阵，矩阵要进行列交换，就在矩阵的右边乘上某个矩阵，在矩阵的右边乘上单位矩阵做相应列交换后的初等矩阵。

 

 

 

 

 

 E₂₁是消元矩阵，现在想找个矩阵取消这次消元。

 E₂₁是单位阵第1行的-3倍加到第2行，现在返回去就是，单位阵的第1行的3倍加到第2行。

 

 

 

 

应该是口误，相当于从行2减去3倍的行1.