训练集、验证集、测试集以及交验验证的理解
在人工智能机器学习中,很容易将“验证集”与“测试集”,“交叉验证”混淆。
训练集、验证集和测试集都有标注吗?
基本上就是从一个数据集中随机分割出来的,所以分布一致,而且都有标注,比如一个人脸数据集分为两部分。
测试集就不同了,通常为真实数据,可能标注都没有或者不告诉你,比如一些比赛中。 训练集和测试集分布可能会有差异。
所以我们用验证集来看模型有没有学到知识,以及会不会过拟合。
用测试集测试模型在真实场景的表现。
大部分情况下,验证集当测试集用了,模型在真实场景表现不好再补充数据。
一、三者的区别
- 训练集(train set) —— 用于模型拟合的数据样本。
- 验证集(development set)—— 是模型训练过程中单独留出的样本集,它可以用于调整模型的超参数和用于对模型的能力进行初步评估。
在神经网络中, 我们用验证数据集去寻找最优的网络深度(number of hidden layers),或者决定反向传播算法的停止点或者在神经网络中选择隐藏层神经元的数量;
在普通的机器学习中常用的交叉验证(Cross Validation) 就是把训练数据集本身再细分成不同的验证数据集去训练模型。
- 测试集 —— 用来评估模最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。
| 类别 | 验证集 | 测试集 |
|---|---|---|
| 是否被训练到 | 否 | 否 |
| 作用 | 用于调超参数,监控模型是否发生过拟合(以决定是否停止训练) | 为了评估最终模型泛化能力 |
| 使用次数 | 多次使用,以不断调参 | 仅仅一次使用 |
| 缺陷 | 模型在一次次重新手动调参并继续训练后所逼近的验证集,可能只代表一部分非训练集,导致最终训练好的模型泛化性能不够 | 测试集为了具有泛化代表性,往往数据量比较大,测试一轮要很久,所以往往只取测试集的其中一小部分作为训练过程中的验证集 |
一个形象的比喻:
训练集-----------学生的课本;学生 根据课本里的内容来掌握知识。
验证集------------作业,通过作业可以知道 不同学生学习情况、进步的速度快慢。
测试集-----------考试,考的题是平常都没有见过,考察学生举一反三的能力。
传统上,一般三者切分的比例是:6:2:2,验证集并不是必须的。
二、为什么要测试集
a)训练集直接参与了模型调参的过程,显然不能用来反映模型真实的能力(防止课本死记硬背的学生拥有最好的成绩,即防止过拟合)。
b)验证集参与了人工调参(超参数)的过程,也不能用来最终评判一个模型(刷题库的学生不能算是学习好的学生)。
c) 所以要通过最终的考试(测试集)来考察一个学(模)生(型)真正的能力(期末考试)。
但是仅凭一次考试就对模型的好坏进行评判显然是不合理的,所以接下来就要介绍交叉验证法
三、交叉验证法(模型选择)
a) 目的
交叉验证法的作用就是尝试利用不同的训练集/验证集划分来对模型做多组不同的训练/验证,来应对单独测试结果过于片面以及训练数据不足的问题。(就像通过多次考试,才通知哪些学生是比较比较牛B的)
交叉验证的做法就是将数据集粗略地分为比较均等不相交的k份,即
然后取其中的一份进行测试,另外的k-1份进行训练,然后求得error的平均值作为最终的评价,具体算法流程如下:
举个例子:假设建立一个BP神经网络,对于隐含层的节点数目,我们并没有很好的方法去确定。此时,一般将节点数设定为某一具体的值,通过训练集训练出相应的参数后,再由交叉验证集去检测该模型的误差;
然后再改变节点数,重复上述过程,直到交叉验证误差最小。
b) 交叉验证算法的具体步骤如下:
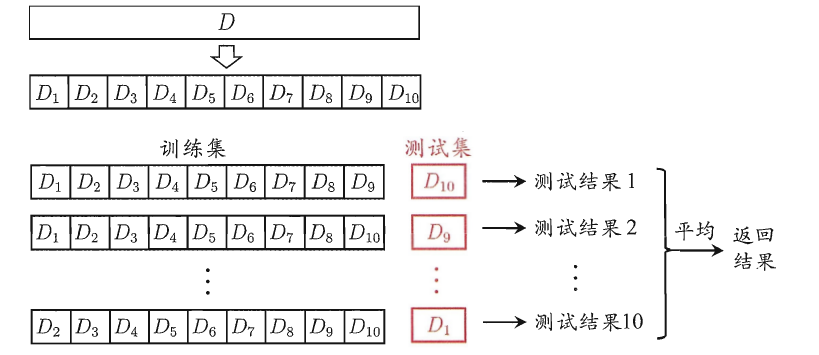
1. 随机将训练数据等分成k份,S1, S2, …, Sk。
2. 对于每一个模型Mi,算法执行k次,每次选择一个Sj作为验证集,而其它作为训练集来训练模型Mi,把训练得到的模型在Sj上进行测试,这样一来,每次都会得到一个误差E,最后对k次得到的误差求平均,就可以得到模型Mi的泛化误差。
3. 算法选择具有最小泛化误差的模型作为最终模型,并且在整个训练集上再次训练该模型,从而得到最终的模型。
K折交叉验证,其主要 的目的是为了选择不同的模型类型(比如一次线性模型、非线性模型、),而不是为了选择具体模型的具体参数。比如在BP神经网络中,其目的主要为了选择模型的层数、神经元的激活函数、每层模型的神经元个数(即所谓的超参数)。每一层网络神经元连接的最终权重是在模型选择(即K折交叉验证)之后,由全部的训练数据重新训练。
目的在模型选择,而非模型训练调整参数。
c) K值的选择
K值的选取是一个偏差与方差的权衡:
K=1时,所有数据用于训练,容易过拟合;
K=N时,相当于留一法LOOCV (Leave-one-out cross-validation ).;
通常建议K=10.,2017年的一项研究给出了另一种经验式的选择方法[3],作者建议 且保证


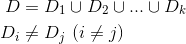


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理