python scipy spatial.KDTree.query用法及代码示例

用法：

KDTree.query(self, x, k=1, eps=0, p=2, distance_upper_bound=inf)

查询kd-tree附近的邻居

参数：

x：array_like, last dimension self.m

要查询的点数组。

k：int, 可选参数

要返回的最近邻点的数量。

eps：nonnegative float, 可选参数

返回近似的最近邻居；第k个返回值保证不超过(k + 1)乘以与第k个最近邻居的距离。

p：float, 1<=p<=infinity, 可选参数

使用哪个Minkowski p-norm。 1是sum-of-absolute值“Manhattan”距离2是通常的欧几里得距离无穷大是maximum-coordinate-difference距离

distance_upper_bound：nonnegative float, 可选参数

仅返回该距离内的邻居。这用于修剪树搜索，因此，如果要执行一 Series nearest-neighbor查询，则可能有助于提供到最近点的最近邻居的距离。

返回值：

d：浮点数或浮点数数组

到最近邻居的距离。如果x具有形状元组+(self.m，)，则如果k为1，则d具有形状元组；如果k大于1，则具有元组+(k，)。丢失的邻居(例如，当k> n或给出distance_upper_bound时)以无限距离表示。如果k为None，则d为形状元组​​的对象数组，其中包含距离列表。不论哪种情况，命中都按距离排序(最接近的优先)。

i：整数或整数数组

self.data中邻居的位置。我与d的形状相同。

例子：

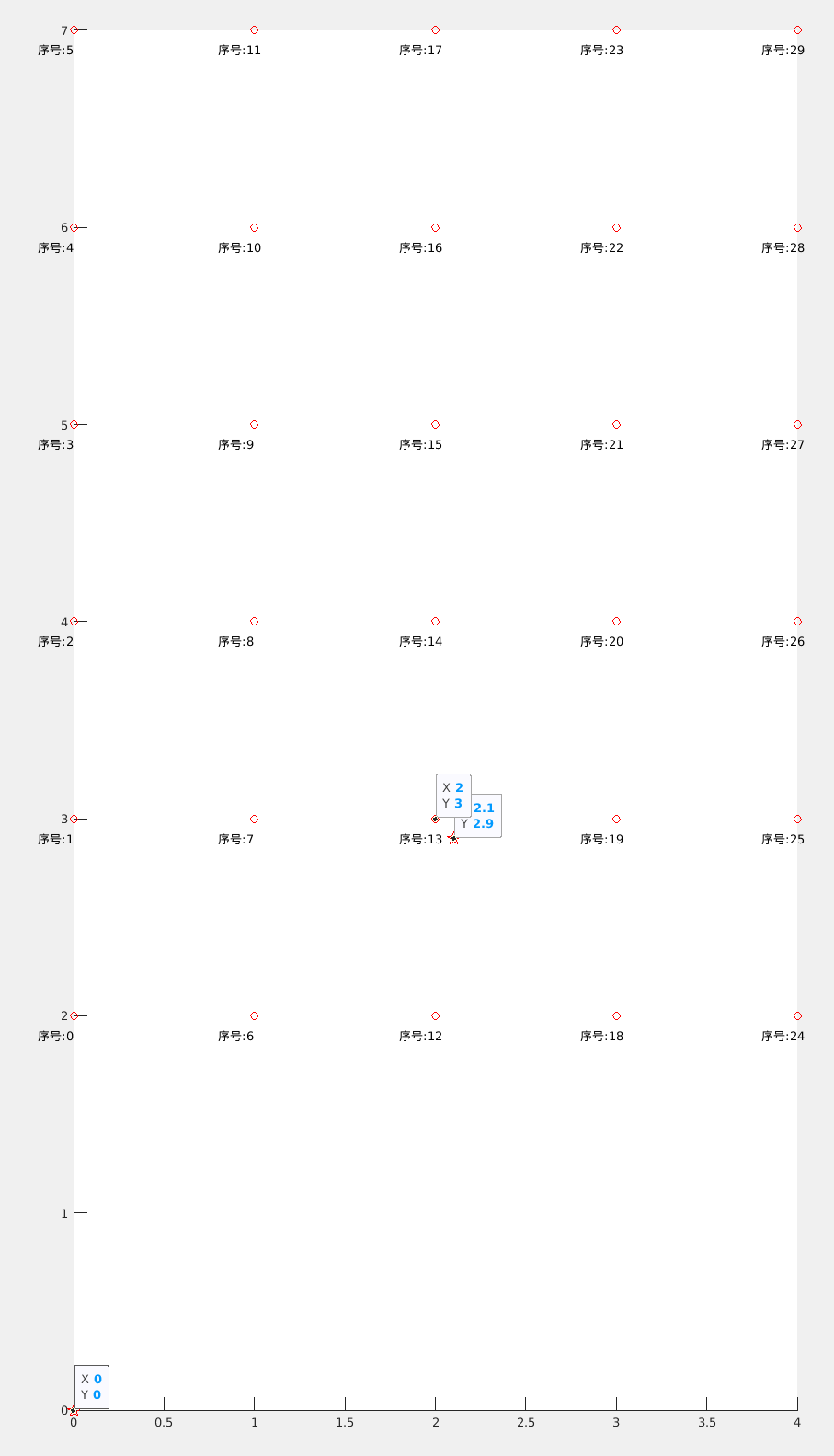
>>> from scipy import spatial
>>> x, y = np.mgrid[0:5, 2:8]
>>> tree = spatial.KDTree(list(zip(x.ravel(), y.ravel())))
>>> tree.data
array([[0, 2],
       [0, 3],
       [0, 4],
       [0, 5],
       [0, 6],
       [0, 7],
       [1, 2],
       [1, 3],
       [1, 4],
       [1, 5],
       [1, 6],
       [1, 7],
       [2, 2],
       [2, 3],
       [2, 4],
       [2, 5],
       [2, 6],
       [2, 7],
       [3, 2],
       [3, 3],
       [3, 4],
       [3, 5],
       [3, 6],
       [3, 7],
       [4, 2],
       [4, 3],
       [4, 4],
       [4, 5],
       [4, 6],
       [4, 7]])
>>> pts = np.array([[0, 0], [2.1, 2.9]])
>>> tree.query(pts)
(array([ 2.        ,  0.14142136]), array([ 0, 13]))
返回值是：离查询点最近的点的距离和索引。(array([ 2. , 0.14142136])是距离，array([ 0, 13]))是索引。
>>> tree.query(pts[0])
(2.0, 0)】
(array([ 2. , 0.14142136])
array([ 0, 13]))

返回值是：离查询点最近的点的距离和索引。

 利用matlab代码可视化：

clc;clear;close all;
dian=[];
for i=0:1:4
    for j=2:1:7
        dian=[dian;[i,j]];
    end
end
pts1=[0,0];
pts2=[2.1,2.9];
figure(1);hold on ;plot(dian(:,1),dian(:,2),'ro');
for k=1:size(dian,1)
    figure(1);hold on ;text(dian(k,1)-0.2,dian(k,2)-0.1,['序号:',num2str(k-1)],'color','k');
end
figure(1);hold on ;plot(pts1(:,1),pts1(:,2),'rp','markersize',11);
figure(1);hold on ;plot(pts2(:,1),pts2(:,2),'rp','markersize',11);

 

源码：

scipy.spatial.KDTree.query的API实现见：[源代码]