正态分布的推导

二项分布跟正态分布有什么关系呢？这就是棣莫弗这人的主要成就之一啦，他1734年发表的一篇关于二项分布文章中提出的，当二项随机变数的位置参数n很大及形状参数p为1/2时，则所推导出二项分布的近似分布函数就是正态分布。当然这个其实就是个极限问题，有兴趣之后我们可以具体讨论。但是这个结果确实是我们直观上可以相像的，当然你还是无法想像，那我们来看看这个计算机的模拟试验。

clc
clear
close all

R3 = binornd(100,0.5,100,1); 
R4 = binornd(1000,0.5,1000,1);
R5 = binornd(10000,0.5,10000,1);

figure
subplot(1,3,1)
histfit(R3)
title('N = 100')
subplot(1,3,2)
histfit(R4)
title('N = 1000')
subplot(1,3,3)
histfit(R5)
title('N = 10000')

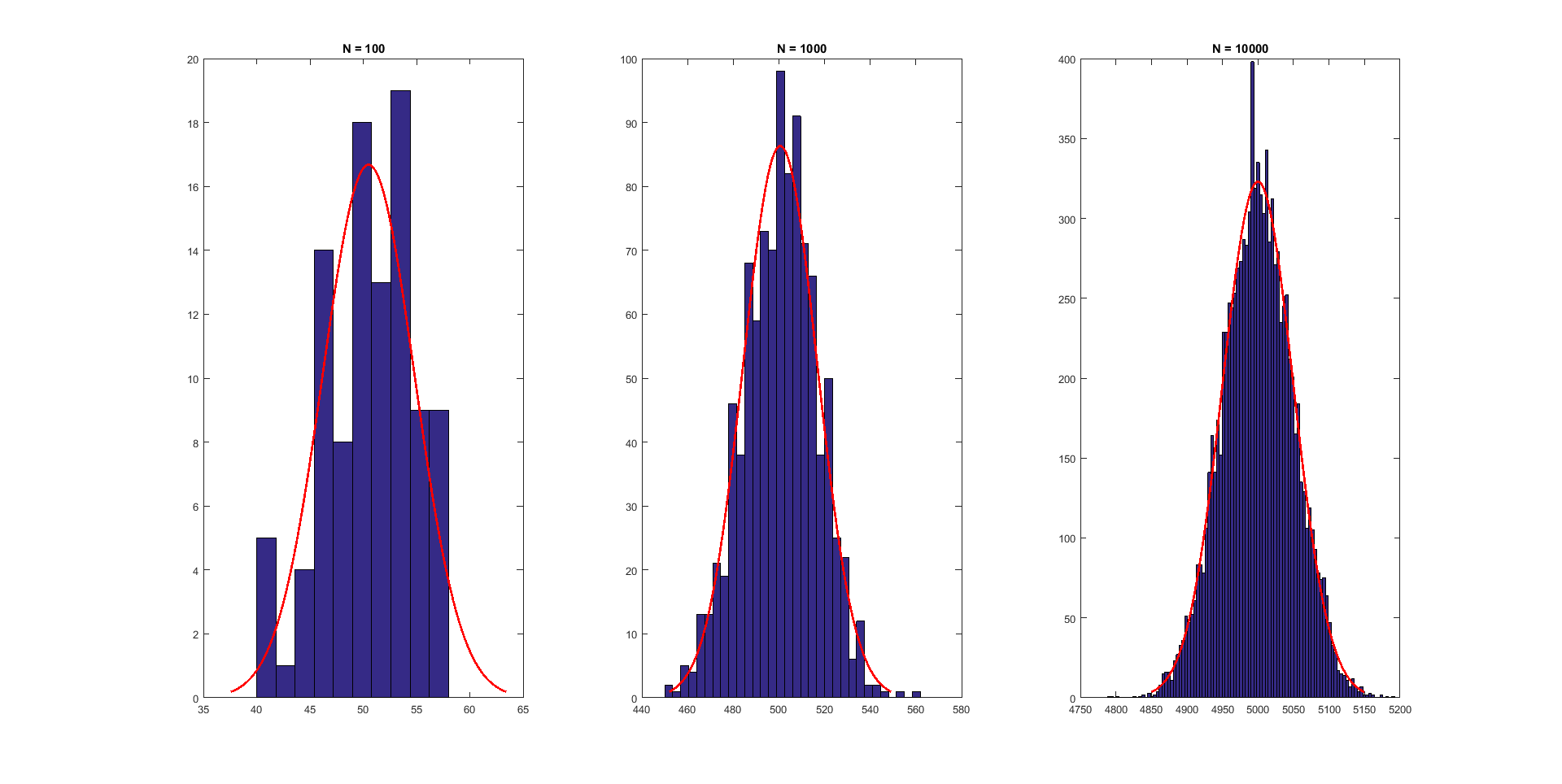
我们的R3,R4,R5分别是从N=100，1000，10000次二项分布中生成的，清晰的看到随着N的增加，这个分布越来越接近我们这个具有代表性的的这个正态分布了。

事实上，这个东西的严格的讲还有特别厉害的名字，中心极限定理， wiki上有一段有趣的历史。Tijms (2004, p.169) 写到：

中心极限定理有着有趣的历史。这个定理的第一版被法国数学家棣莫弗发现，他在1733年发表的卓越论文中使用正态分布去估计大量抛掷硬币出现正面次数的分布。这个超越时代的成果险些被历史遗忘，所幸著名法国数学家拉普拉斯在1812年发表的巨著 Théorie Analytique des Probabilités中拯救了这个默默无名的理论。

拉普拉斯扩展了棣莫弗的理论，指出二项分布可用正态分布逼近。但同棣莫弗一样，拉普拉斯的发现在当时并未引起很大反响。直到十九世纪末中心极限定理的重要性才被世人所知。1901年，俄国数学家里雅普诺夫用更普通的随机变量定义中心极限定理并在数学上进行了精确的证明。如今，中心极限定理被认为是(非正式地)概率论中的首席定理。

然而，正态分布真正走入人们视线的并不是由这个无聊的投硬币试验所得的二项分布的逼近，而是实实在在的工程误差分析中应用。据说wiki说，拉普拉斯在误差分析试验中使用了正态分布。勒让德于1805年引入最小二乘法这一重要方法；而高斯则宣称他早在1794年就使用了该方法，并通过假设误差服从正态分布给出了严格的证明。

高斯对正态分布的导出准备

之前我们说到高斯对测量误差研究中发现了正态分布，并且这项研究也成为了当代统计学的中重要的思想--最大似然发现的源头。下面我们来仔细看看，他是如何导出这个完美的分布的。

首先我们要解释几个概念，第一个是似然（Likelihood）。什么是似然，简单通俗的来讲就是，一系列的概率密度函数的乘积，说白了也就是还是一种特别的复合的“概率”。比如对于正态分布，如果有独立同分布的观察值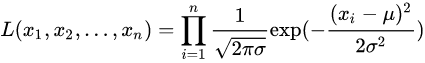 $x_1,x_2,\cdots,x_n$ ,则其的似然为：

当然，我们也可以看到对于正态分布，这里还依赖于两个参数，就是 $\mu,\sigma$ 。所以我们其实也可以将这个似然看成关于 $\mu,\sigma$ 的二元函数。当然在给其中一个参数的情况下，我们也可以将其看成关于另一个的函数。另外，从数值上讲概率是在[0，1]，所以n个连乘之后也还是在[0，1]。

第二点是最大似然（Maximum Likelihood）,刚才说到对对正态这个似然，当然在给其中一个参数的情况下，我们也可以将其看成关于另一个的函数。因而，如果我们给定一个标准，那么是不是可以基于观测值对其中的未知参数进行估计呢？这是个非常朴素想法，就好比方程的思想，原本一个函数，给定自变量，那么对应的函数值自然可以计算。反过来，若是给定一定函数值，理论上我们也希望试图找到对应的自变量。这个想法再进一步就是，给定一个标准，比如最大，最小，我们基于这个标准，也试图去寻找对应达到标准（比如最大，最小函数值）所对应的自变量，这就是参数估计的思想。回到最大似然的核心，在这里这个标准就是使得似然函数（关于某一或某一些参数的）最大，然后去估计对应的参数（基于观测值）的值。至于为什么选择似然函数呢，其实主要也是因为似然函数朴素简单的表达出一种概率，一个基于n次观测的整体的概率，这样的情况下，我们自然朴素的认为或者是希望，似然中包含的合理的参数应该是使得我们整体的概率最大的一个或者是一组，因此才被我们观测到。

好了，介绍这个这个，我们继续重新回到正题，如何基于一些假设导出正态分布。实际的测量中，若 $\mu$ 是分布均值的真实值，当然真实值我们永远都不可能知道，因为我们活在一个误差的世界，然后现在希望根据观测值 $x_1,x_2,\cdots,x_n$ 尽可能的去估计它。首先我们记观察误差 $x_i - \mu$ 的分布密度函数为 $p(x_i -\mu)$ ，然后给以下假设（数学的世界充满假设，没有假设的数学，如没有根的浮萍，毫无意义）。

$p(x)$ 关于 $x=0$ 对称，且对于一切 $x$ 成立 $p(x)>0$ .
$p(x)$ 具有连续的导函数。

下面我们来考察这两个假设的合理性，首先 $p(x)$ 关于 $x=0$ 对称，这个非常合理，因为我们的似然误差分布密度为 $p(x_i -\mu)$ ，也就是观测值与真实均值的差，这个自然在左在右可能性一样喽，不然这个观测试验也就有偏颇了，当然另一个理由也就是经验了。再说非负性要求，这个也是必须的，概率么自然是非负的啦。第二条，连续的导函数，这个自然主要是为了推倒的方便啦。

由于我们的观察误差 $x_i - \mu$ 的分布密度函数为 $p(x_i -\mu)$ ，那么此时的似然函数就是

$L(\mu) = \prod_{i=1}^n p(x_i - \mu)$

实际上，这个似然函数刻画了这组观测值落在真实均值 $\mu$ 附近的可能性大小。当然此处高斯还给出了一个重要的假设：

观察值的平均值 $\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i$ 作为未知参数 $\mu$ 的估计值时使得似然 $L(\mu)$ 最大。

事实上，下面的推导主要还是依赖于这个假设。回头看看这个假设，其实也是符合逻辑和直观感受的，这表明观测的均值作为一个理论均值可以让似然函数最大。

高斯对正态分布的导出的具体过程

若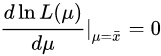 $\bar{x}$ 使得似然函数似然 $L(\mu)$ 最大，则根据数学分析（当然大多数人你们学的是微积分，或者是高等数学）的结论，它的必要条件是关于参数 $\mu$ 导函数在 $\mu = \bar{x}$ 处为0。

..................................... (1)

此时，我们记 $\frac{d \ln p(x)}{d x} = g(x)$ ,根据复合函数的求导法则（链式法则），具体是针对对数函数的那个，我们可以得到 $g(x) = \frac{p'(x)}{p(x)}$ ，同时根据连续函数假设，我们可以对等式（1）进行简化，

其中第一个等号到第二个等号用的是对数函数的性质（积的对数函数等于对数函数的和），第二等式到第三个么是求导的性质（和的导数等于导数的和），第三到第四么就是g(x)的定义以及复合函数求导法则，之后就是带入啦。所以最后我们可以得到的是

$\sum_{i=1}^n g(x_i - \bar{x}) = 0$ .....................................(2)

若此时，我们简化考虑，令n = 2, 则方程(2)进一步简化可以得到

$g(x_1 - \bar{x}) + g(x_2 - \bar{x}) = 0$

由于 $x_1 -\bar{x} = -(x_2 -\bar{x})$ 以及， $x_1,x_2$ 的任意性，我们可以得到g(x)是个中心对称函数，即 $g(x) = -g(-x)$ 对一切实数x成立。

另外，当n=3时，方程（2）可以简化得到

$g(x_1 - \bar{x}) + g(x_2 - \bar{x}) + g(x_3-\bar{x})= 0$

由于 $x_1 -\bar{x} = -[(x_2 -\bar{x}) + (x_3 - \bar{x})]$ 以及， $x_1,x_2,x_3$ 的任意性，我们可以得到对一切实数 $x,y$ 成立，

$g(x) +g(y) = g(x+y)$

这也是个大名鼎鼎的方程，叫柯西函数方程，这类方程在有理数范围内，可以得到唯一的通解(当然根据连续性联系，结合有限覆盖原理可以得出在实数域内也有唯一的此种解，比较复杂，这里就不详细讨论了)， $g(x) = b x$ 。因此，很快我们可以得到一个微分方程，即

$\frac{p'(x)}{p(x)} = bx \Rightarrow \frac{\mathrm{d} p(x)}{p(x)} =b x \cdot \mathrm{d} x$ , 这里可能需要一些简单的微分方程的知识就可以直接得到，不过这里我们可以直观的想一下，哪个函数的的求导之后会出现左边的形式呢？

作者：蓦风星吟
链接：https://zhuanlan.zhihu.com/p/24437232
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

对嘛，ln函数呀！ $\mathrm{d} \ln p(x) = \frac{\mathrm{d} p(x)}{p(x)}$ 。然后再想一下，什么函数的导数会是右边形式呢？

嗯，好像二次函数的求导之后就是这样哦！所以嘛，最后这个方程结果是：

$\ln p(x) = \frac{b}{2}x^2 + c \Rightarrow p(x) = e^{\frac{b}{2}x^2 + c}, -\infty <x < \infty$

由于 $p(x)$ 是密度函数，需要大于0小于1，因此我们需要令 $b<0$ ，否则这样的指数函数分分钟大于1了哈，不妨我们记 $b = - \frac{1}{\sigma^2}$ ，则

$p(x) = K e^{-\frac{x^2}{2\sigma^2}}, \qquad -\infty < x<\infty$ .............................................................................(3)

当然不要忘记了，概率密度函数的在可行范围内的积分需要为1哦，即 $\int_{-\infty}^{\infty} p(x) dx = 1$ ，结合方程（3）可以解出 $K = \frac{1}{\sqrt{2\pi\sigma^2}}$ 。什么？这个积分不会算么？啊？我想想，这个还是去找个多元微积分教材看看吧，对了，还有个好办法，做题神器，高级计算器，maple,非常好用，下面有连接，输入公式，再复杂的微积分题也可以算出来（不对，其实不一定哈，不过至少你们课本上的题无论常义积分还是反常积分都是秒算哈，不过用多了你的数学基础估计就废了，考试也不用指望了），所以想要打基础好好学习把，不过想要快速解决问题，这个一定是上选！

Maple 2016 - Technical Computing Software for Engineers, Mathematicians, Scientists, Instructors and Students - Maplesoft

最后系数算出来之后我们就得到了z著名的误差公式，当然也是正态分布的密度函数，看着是不是很眼熟，对，没错，我想你应该有印象，对，你应该记住了，就是这个完美的分布！

$p(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{x^2}{2\sigma^2}}, \qquad -\infty < x<\infty$

参考文献

李贤平, 概率论基础 (第三版). 高等教育出版社, 2010.

作者：蓦风星吟
链接：https://zhuanlan.zhihu.com/p/24437232
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

posted on 2020-08-05 15:36 一杯明月阅读(5261) 评论(0) 编辑收藏举报