插值和拟合

2020.4.8

matlab插值

预先选用什么插值方法，可以关注曲线的实际形状。比如道路标线的话，可以选用分段线性插值，因为道路标线一般是直的，卫星轨道的话可以选择三次多项式插值。因为卫星轨道是椭圆。

clc;clear;close all;
x=0:2*pi;
y=sin(x);
xx=0:0.5:2*pi;

%interp1对sin函数进行分段线性插值，调用interp1的时候，默认的是分段线性插值
y1=interp1(x,y,xx);
subplot(2,2,1);plot(x,y,'o',xx,y1,'r')
title('分段线性插值')

%临近插值
y2=interp1(x,y,xx,'nearest');
subplot(2,2,2);
plot(x,y,'o',xx,y2,'r');
title('临近插值')

%球面线性插值
y3=interp1(x,y,xx,'spline');
subplot(2,2,3);
plot(x,y,'o',xx,y3,'r')
title('球面插值')

%三次多项式插值法
y4=interp1(x,y,xx,'cubic');
subplot(2,2,4);
plot(x,y,'o',xx,y4,'r');
title('三次多项式插值')

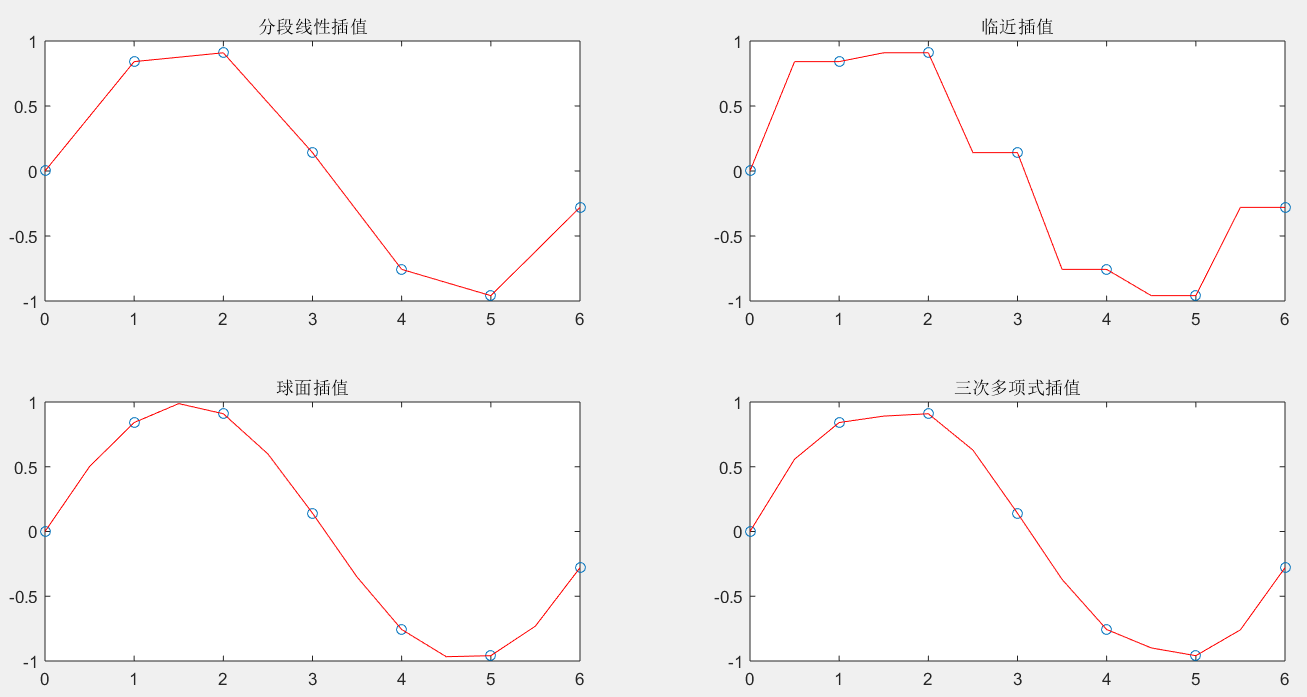
(1) Nearest方法速度最快，占用内存最小，但一般来说误差最大，插值结果最不光滑。

(2) Spline三次样条插值是所有插值方法中运行耗时最长的，插值函数及其一二阶导函数都连续，是最光滑的插值方法。占用内存比cubic方法小，但是已知数据分布不均匀的时候可能出现异常结果。

(3) Cubic三次多项式插值法中，插值函数及其一阶导数都是连续的，所以插值结果比较光滑，速度比Spline快，但是占用内存最多。
————————————————
版权声明：本文为CSDN博主「风翼冰舟」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/zb1165048017/article/details/48343507

2020.4.6

一、插值和拟合的区别

什么叫插值？插值是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。

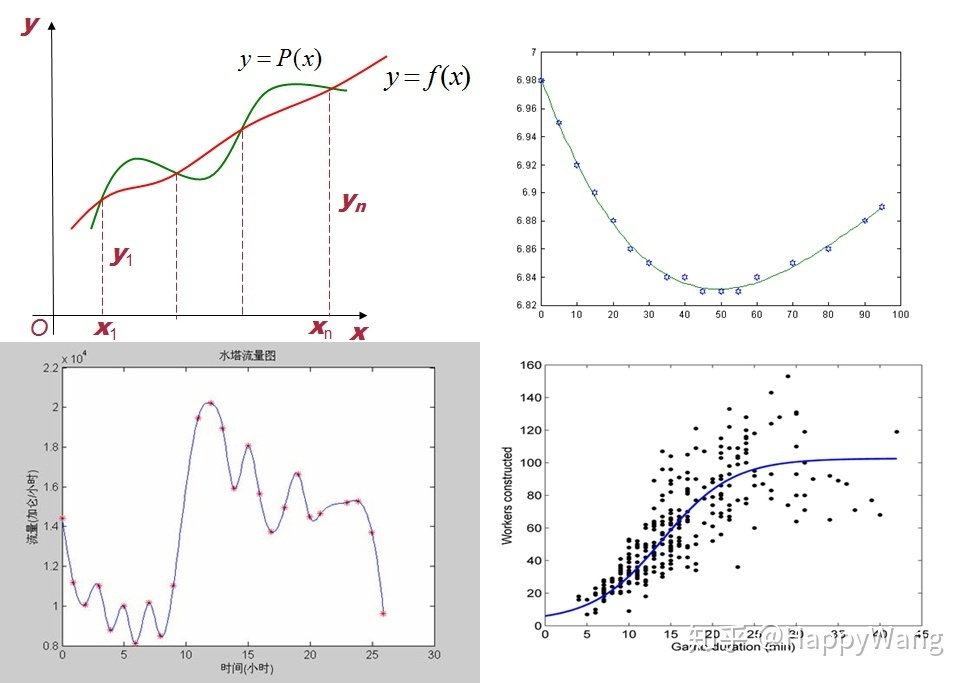
首先插值和拟合都是根据某个未知函数（或已知但难于求解的函数）的几个已知数据点求出变化规律和特征相似的近似曲线的过程。但是插值法要求的是近似的曲线需要完全经过数据点，而拟合则是得到最接近的结果，强调最小方差的概念。插值和拟合的区别如下图所示^[1]（其中左边为插值，右边为拟合）：

二、常见插值法

1.基本概念

设函数 $y=f(x)$ 有n个已知数据点 $[x_i,y_i],i=0,1,…,n$ ，若存在一简单函数 $P(x)$ ，使 $P(x_i)=y_i,i=1,2,…,n$ 成立。则 $P(x)$ 为 $f(x)$ 的插值函数，点 $x_i$ 为插值节点，求 $P(x)$ 的方法称为插值法。

2.拉格朗日插值（可以参考：https://www.zhihu.com/question/58333118/answer/262507694）

在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法。许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解。如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日（插值）多项式。数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现^[1]，不久后（1783年）由莱昂哈德·欧拉再次发现。1795年，拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法，从此他的名字就和这个方法联系在一起^[2]。

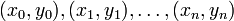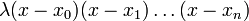对于给定的若n+1个点 $(x_0, y_0),(x_1, y_1),\ldots,(x_n, y_n)$ ，对应于它们的次数不超过n的拉格朗日多项式 $\scriptstyle L$ 只有一个。如果计入次数更高的多项式，则有无穷个，因为所有与 $\scriptstyle L$ 相差 $\lambda (x-x_0)(x-x_1)\ldots(x-x_n)$ 的多项式都满足条件。

Lagrange插值多项式的公式如下：

基函数：

$\begin{aligned} l_{i}(x) &=\frac{\left(x-x_{0}\right) \cdots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right) \cdots\left(x-x_{n}\right)}{\left(x_{i}-x_{0}\right) \cdots\left(x_{i}-x_{i-1}\right)\left(x_{i}-x_{i+1}\right) \cdots\left(x_{i}-x_{n}\right)} \\ &=\prod_{j=0 \atop j \neq i}^{n} \frac{x-x_{j}}{x_{i}-x_{j}}, \quad(i=0,1, \cdots, n) \end{aligned}$

插值多项式：

$L_{n}(x)=\sum_{i=0}^{n} y_{i} l_{i}(x)=\sum_{i=0}^{n} y_{i}\left(\prod_{j=0 \atop j \neq i}^{n} \frac{x-x_{j}}{x_{i}-x_{j}}\right)$

插值余项：

$R_{n}(x)=f(x)-L_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !} \omega_{n+1}(x), \xi \in(a, b)$

当 $\max\limits_{a\leq{x}\leq{b}}|f^{n+1}(x)|=M_{n+1}$ 时，截断误差界是：

$R_{n}(x)=\frac{M^{(n+1)}(x)}{(n+1) !} \omega_{n+1}(x)$

其中： $\omega_{n+1}(x)=\prod_{i=0}^{n}\left(x-x_{j}\right)$

范例

假设有某个多项式函数 $f ，已知它在三个点上的取值为：$

$f (4) = 10$
$f (5) = 5.25$
$f (6) = 1$

要求 $f (18)的值。$

首先写出每个拉格朗日基本多项式：

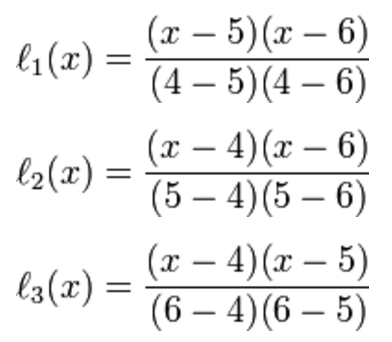
matlab代码：

function y=Lagrange(x0,y0,x)
%输入：x0:节点变量数据
%      y0:节点函数值
%      x:插值数据
%输出：y:插值函数值
    n=length(x0);m=length(x);
    for i=1:m
        z=x(i);
        s=0.0;
        for k=1:n
            p=1.0;
            for j=1:n
                if j~=k
                    p=p*(z-x0(j))/(x0(k)-x0(j));
                end
            end
            s=p*y0(k)+s;
        end
        y(i)=s;
    end
end

例1：设 $f(x)=ln(x)$ ,并给出如下节点数据

x0=[0.4,0.5,0.7,0.8]

y0=[-0.916291,-0.693147,-0.356675,-0.223144]

估计x=0.6的值

带入Lagrange()函数，得到 $y=-0.5100$ ，实际值： $ln(0.6)= -0.5108$

优点与缺点

拉格朗日插值法的公式结构整齐紧凑，在理论分析中十分方便，然而在计算中，当插值点增加或减少一个时，所对应的基本多项式就需要全部重新计算，于是整个公式都会变化，非常繁琐^[5]。这时可以用重心拉格朗日插值法或牛顿插值法来代替。此外，当插值点比较多的时候，拉格朗日插值多项式的次数可能会很高，因此具有数值不稳定的特点，也就是说尽管在已知的几个点取到给定的数值，但在附近却会和“实际上”的值之间有很大的偏差（如右下图）^[6]。这类现象也被称为龙格现象，解决的办法是分段用较低次数的插值多项式。

2.分段线性插值：

2.1基本原理：

将每两个相邻的节点用直线连起来，如此形成的一条折线就是分段线性插值函数。计算点的插值时，只用到左右的两个节点，计算量与节点个数n（初始值x0，y0的长度,n=length(x0)）无关，而拉格朗日插值与n值有关。分段线性插值中n越大，分段越多，插值误差越小。

2.2 Matlab实现分段线性插值：

用matlab实现分段线性插值不需要自己手动编写函数，matlab有现成的一维插值函数interp1

y=interp1(x0,y0,x,'method')

该式可以根据X，Y的值来计算函数在X1处的值。其中X，Y是两个等长的已知向量，分别表示采样点和采样值。X1是一个向量或标量，表示要插值的点。

method指定插值方法，其值可为：

linear：线性插值（默认）线形插值，默认方法。将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。

nearest：最近项插值，最近点插值。选择最近样本点的值作为插值数据。

spline：逐次3次样条插值，每一个分段内构造一个三次多项式，使其插值函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。

cubic：保凹凸性 3 次插值

pchip: 分段3次埃尔米特插值。采用分段三次多项式，除满足插值条件，还需满足在若干节点处相邻段插值函数的一阶导数相等，使得曲线光滑的同时，还具有保形性。

所有插值方法都要求x0单调。

MATLAB的二维插值函数为interp2(),

调用格式：y1 = interp2(X,Y,Z,X1,Y1,method)

其中X，Y两个向量，表示两个参数的采样点，Z是采样点对应的函数值。X1，Y1是两个标量或向量，表示要插值的点。指定的算法method计算二维插值。

’linear’：双线性插值算法(缺省算法);
’nearest’：最临近插值;
’spline’：三次样条插值;
’cubic’：双三次插值。

3.三次样条插值：

使用三次样条插值有两种方法：其中一种就是第二种插值方式（分段线性插值），只需要将method修改为spline即可实现。

还有一种实现方式如下：

pp=csape(x0,y0);

y=ppval(pp,x);

其中x0，y0，x与前面含义相同，返回值y即插值结果。

4.彩蛋（例题）：

表1给出的 x, y 数据位于机翼断面的下轮廓线上，假设需要得到 x 坐标每改变0.1 时的 y 坐标。试完成加工所需数据，画出曲线。要求用 Lagrange、分段线性和三次样条三种插值方法计算。

表1

x 0 3 5 7 9 11 12 13 14 15
y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
解：编写代码如下：

clear,clc;close all;
x0=[0,3,5,7,9,11,12,13,14,15];
y0=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];
x1=[0:0.1:15];

%拉格朗日插值
y1=lagrange(x0,y0,x1);
subplot(1,3,1);hold on;plot(x0,y0,'ro');
subplot(1,3,1);hold on;plot(x1,y1,'b.');%axis equal;axis off;
title('拉格朗日插值')
%分段线性插值
y2=interp1(x0,y0,x1);
subplot(1,3,2);hold on;plot(x0,y0,'ro');
subplot(1,3,2);hold on;plot(x1,y2,'b.');%axis equal;axis off;
title('分段线性插值')
%三次样条插值
y3=interp1(x0,y0,x1,'spline');
subplot(1,3,3);hold on;plot(x0,y0,'ro');
subplot(1,3,3);hold on;plot(x1,y3,'b.');%axis equal;axis off;
title('三次样条插值');
function y=lagrange(x0,y0,x)
%输入：x0:节点变量数据
%      y0:节点函数值
%      x:插值数据
%输出：y:插值函数值
    n=length(x0);m=length(x);
    for i=1:m
        z=x(i);
        s=0.0;
        for k=1:n
            p=1.0;
            for j=1:n
                if j~=k
                    p=p*(z-x0(j))/(x0(k)-x0(j));
                end
            end
            s=p*y0(k)+s;
        end
        y(i)=s;
    end
end

结果图为:

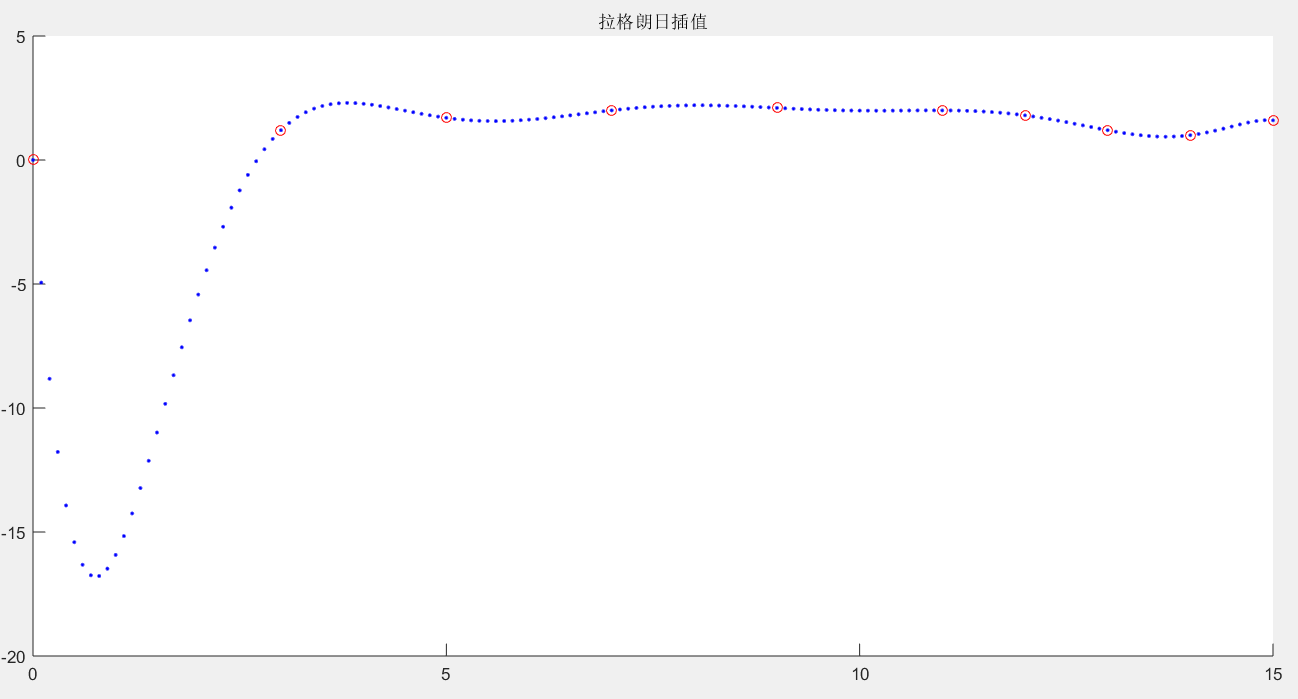
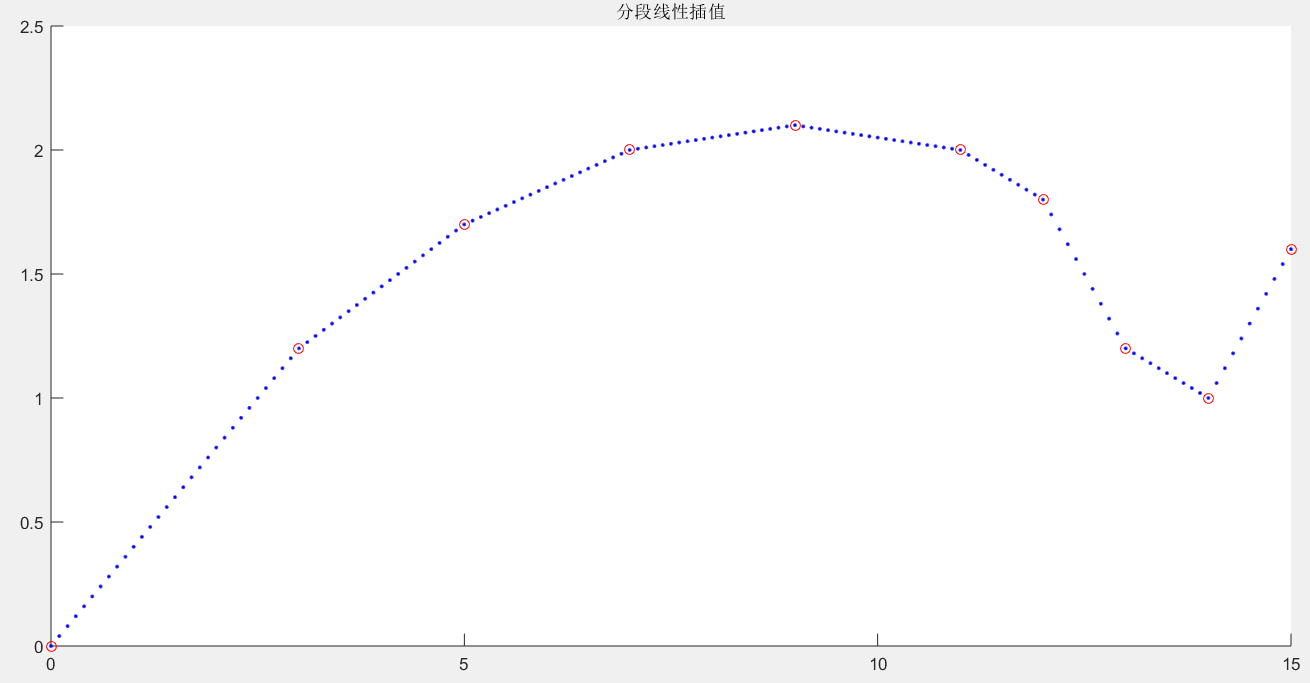
红色圆圈是原始数据点，蓝色点点是插值点（包含插值位置和插值值）。

由图可知：拉格朗日插值误差较大，插值大量点的时候不建议使用。分段线性插值结果最好，使用的是method是linear（默认）。三次样条插值有点误差，但不是很大，得到的曲线比较光滑。

————————————————
版权声明：本文为CSDN博主「Da_wan」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Da_wan/article/details/82223572

3.Newton插值

上面介绍的拉格朗日插值多项式，当插值节点增减时，计算要全部进行，很不方便，所以提出一种Newton插值。

（1）差商和差分的性质

一阶差商（均差）：

$f\left[x_{i}, x_{j}\right]=\frac{f\left(x_{i}\right)-f\left(x_{j}\right)}{x_{i}-x_{j}}$

二阶差商（均差）：一阶差商的差商

$f\left[x_{i}, x_{j},x_{k}\right]=\frac{f\left[x_{i}, x_{j}\right]-f\left[x_{j}, x_{k}\right]}{x_{i}-x_{k}}$

$k$ 阶差商（均差）：

$f\left[x_{0}, x_{1}, \cdots, x_{k}\right]=\frac{f\left[x_{0}, x_{1}, \cdots, x_{k-1}\right]-f\left[x_{1}, x_{2}, \cdots, x_{k}\right]}{x_{0}-x_{k}}$

（2）Newton插值多项式

$\begin{aligned} N_{n}(x) &=f\left(x_{0}\right)+\left(x-x_{0}\right) f\left[x_{0}, x_{1}\right]+\cdots \\ &+\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n-1}\right) f\left[x_{0}, x_{1}, \cdots, x_{n}\right] \end{aligned}$

（3）误差

$\begin{aligned} R_{n}(x) &=\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n}\right) f\left[x_{0}, x_{1}, \cdots, x_{n}\right] \end{aligned}\\=w_{n+1}(x)f[x,x_{0},x_{1},…,x_{n}]\\=\frac{M^{(n+1)}(x)}{(n+1) !} \omega_{n+1}(x)$

(4)差商与导数的关系

$f\left[x_{0}, x_{1}, \cdots, x_{k}\right]=\frac{f^{n}(\xi)}{n!}$

matlab代码如下：

function [YY,y]=newton_chazhi(X,Y,x,M)
%输入为：X-插值点的x轴向量
%Y-插值点的y轴向量
%需要求解的x变量
%M为多项式次数
%输出YY为差分表
%y是x对应的因变量
m=length(X);
YY=zeros(m);
YY(:,1)=Y;
%求查分表
for i=2:m
    for j=i:m
        YY(j,i)=(YY(j,i-1)-YY(j-1,i-1))/(X(j)-X(j-i+1));
    end
end
y=Y(1);
%计算newton插值公式
for i=1:M
    xl=1;
   for j=1:i
       xl=xl*(x-X(j));
   end
   y=y+xl*YY(i+1,i+1);
end
end


function [YY,y]=main()
X=[0.40,0.55,0.65,0.80,0.90,1.05];
Y=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];
x=0.596;
M=4;
[YY,y]=newton_chazhi(X,Y,x,M);
end

4.三次Hermite插值

$P(x)=f(x_0)+f[x_0,x_1](x_1-x_0)+f[x_0,x_1,x_2](x-x_0)(x-x_1)+A(x-x_0)(x-x_1)(x-x_2)$

其中： $A=\frac{f'(x_1)-f[x_0,x_1]-(x_1-x_0)f[x_0,x_1,x_2]}{(x_1-x_0)(x_1-x_2)}$ ，余项表达式：

$R(x)=\frac{1}{4!}f^{(4)}(\xi)(x-x_0)(x-x_1)^2(x-x_2)$

用Hermite进行插值时需要有确定的三个数据点以及中间点的一阶导数。

例：给定 $f(x)=x^{3/2},x_0=\frac{1}{4},x_1=1,x_2=\frac{9}{4},$ 求三次样条插值多项式 $P(x)$ ，及余项表达式。

matlab代码：

function y=hermiter_chazhi(X,Y,x1,x)
%求差分表
m=length(X);
YY=zeros(m);
YY(:,1)=Y;
for i=2:m
    for j=i:m
        YY(j,i)=(YY(j,i-1)-YY(j-1,i-1))/(X(j)-X(j-i+1));
    end
end
%求A
A=x1-YY(2,2)-(X(2)-X(1))*YY(3,3);

%求插值
y=Y(1)+YY(2,2).*(x-X(1))+YY(3,3).*(x-X(1)).*(x-X(2))+A.*(x-X(1)).*(x-X(2)).*(x-X(3));
end

function y=main_her()
x=[1/4:0.01:9/4];
f=x.^(3/2);
X=[1/4,1,9/4];
Y=[1/8,1,27/8];
x1=3/2;
y=hermiter_chazhi(X,Y,x1,x);

plot(x,y,"r")
grid on
hold on 
plot(x,f,"b")
scatter(X,Y)
legend("插值曲线","实际曲线")
end

5.三次样条插值

三次样条插值参考下面的博客：

HappyWang：轨迹生成--三次样条插值zhuanlan.zhihu.com

三、常见的拟合方法

HappyWang：回归预测（1）--线性回归和多项式拟合zhuanlan.zhihu.com

参考

^https://www.zhihu.com/question/24276013

作者：HappyWang
链接：https://zhuanlan.zhihu.com/p/98431641
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

posted on 2020-04-05 22:13 一杯明月阅读(2928) 评论(0) 编辑收藏举报