高斯滤波
高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
高斯滤波后图像被平滑的程度取决于标准差。它的输出是临域像素的加权平均，同时离中心越近的像素权重越高。因此，相对于均值滤波（mean filter）它的平滑效果更柔和，而且边缘保留的也更好。高斯滤波被用作为平滑滤波器的本质原因是因为它是一个低通滤波器，而且大部份基于卷积平滑滤波器都是低通滤波器。GAUSS 滤波算法克服了边界效应，因而滤波后的图像较好。
原文链接：https://blog.csdn.net/weixin_41445387/article/details/90142404
其中μ是x的均值,δ是x的方差。当中心点为原点时，u为0，此时的公式如下：
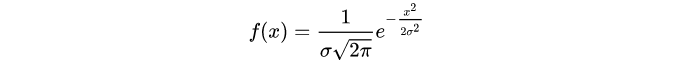
根据一维高斯函数，可以推导出二维高斯函数（中心为原点）：
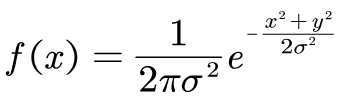
通过上述两个维度的高斯滤波器函数可以得到下图的函数图像。其中的大小决定了高斯函数的宽度， σ越大函数图像跨幅越宽，反之则越窄。
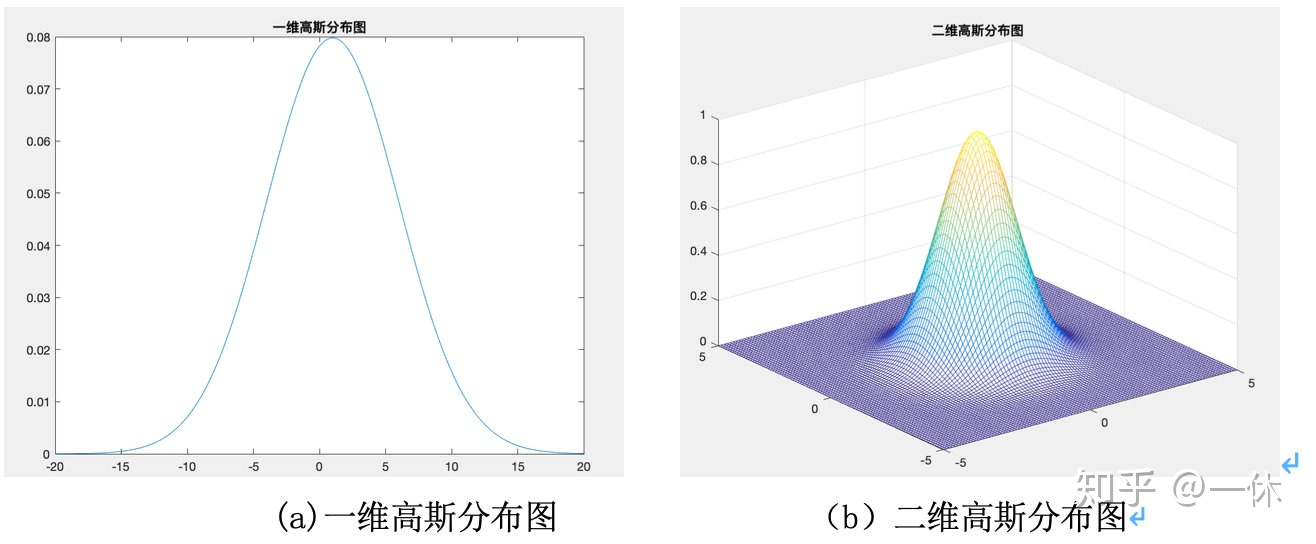
在图像处理中，高斯滤波一般有两种实现方式，一是用离散化窗口滑窗卷积，另一种通过傅里叶变换。最常见的就是第一种滑窗实现，只有当离散化的窗口非常大，用滑窗计算量非常大（即使用可分离滤波器的实现）的情况下，可能会考虑基于傅里叶变化的实现方法。
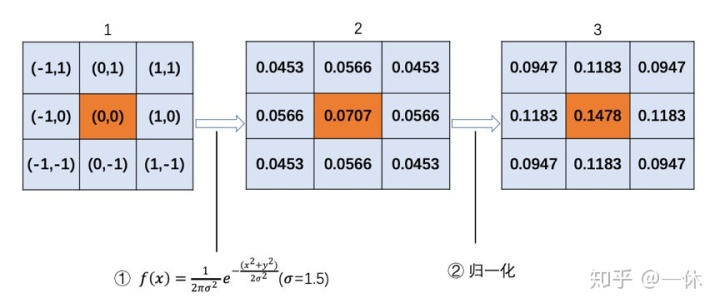
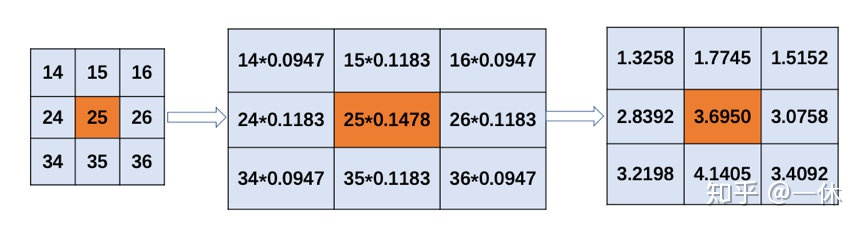
通过上述步骤计算出高斯核，基于该高斯核便可进行高斯滤波操作。假设现有9个像素点，灰度值（0-255）如下图中第一个卷积核所示，计算图中中心点的滤波后的值。每个像素点乘以相对应的权重值，得到最终的分布值。将这9个像素的值相加得到的结果，就是中心位置图像滤波后的值。对所有点重复这个过程，就得到了高斯滤波后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯滤波。
讲解完卷积核的过程，通过代码具体的实现高斯滤波。由于高斯滤波主要针对高斯噪声表现的比较好，所有gasuss_noise在原始图片中添加随机噪声，其中的参数mean和var对应二维高斯核函数的 和 。调用了opencv的GaussianBlur函数，针对下面代码中的（3，3）是高斯矩阵的长和宽，0是高斯核的标准差是0，具体代码如下：
def gasuss_noise(img, mean=0, var=0.005): ''' 添加高斯噪声 mean : 均值 var : 方差 ''' image = img.copy() image = np.array(image/255, dtype=float) noise = np.random.normal(mean, var ** 0.5, image.shape) out = image + noise if out.min() < 0: low_clip = -1. else: low_clip = 0. out = np.clip(out, low_clip, 1.0) out = np.uint8(out*255) return out #读取图片 gasuss_noise_img = gasuss_noise(img) #均值滤波 gasuss_filter_img = cv2.GaussianBlur(img, (3, 3), 1.1) gasuss_filter_img1 = cv2.GaussianBlur(gasuss_noise_img, (3, 3), 1.1) gasuss_filter_img2 = cv2.GaussianBlur(gasuss_noise_img, (9, 9), 1.1) ## 显示 plt.figure(figsize=(15, 10)) plt.subplot(2, 2, 1), plt.imshow(img) plt.axis('off'); plt.title('原图') plt.subplot(2, 2, 2), plt.imshow(gasuss_noise_img) plt.axis('off'); plt.title('添加随机高斯噪声') plt.subplot(2, 2, 3), plt.imshow(gasuss_filter_img1) plt.axis('off'); plt.title('高斯核为3') plt.subplot(2, 2, 4), plt.imshow(gasuss_filter_img2) plt.axis('off'); plt.title('高斯核为9') plt.show()
运行代码得到，通过matplotlib函数可以得到下图所示的图像。从结果图中可以看出卷积核越大，高斯噪声过滤的效果越好，但是最终的结果图也就越模糊，清晰度越差。具体过滤需要结果过滤效果和图像清晰度综合选取滤波卷积核尺寸半径。
双边滤波
双边滤波（Bilateral filter）是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折衷处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的。具有简单、非迭代、局部的特点。
双边滤波器之所以能够做到在平滑去噪的同时还能够很好的保存边缘（Edge Preserve），是由于其滤波器的核由两个函数生成：空间域核（又称定义域核，空间系数或空间域）和值域核(又称像素范围域)。
空间域核是由像素位置欧式距离决定的模板权值 ，公式如下：
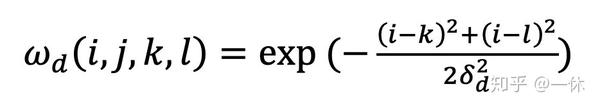
其中i,j,k,l代表的是坐标点q(i,j)和 p(k,l)。q(i,j)是卷积核模板窗口的其他系数的坐标；p(k,l)为模板窗口的中心坐标点；p(k,l)为高斯函数的标准差。为高斯函数的标准差该核函数属于上面讲解的高斯核函数。从第一个公式可知，
是计算临近点q到中心点p的临近程度，因此空间域核 是用于衡量空间临近的程度。
值域核是由像素值的差值决定的模板权值，公式如下：
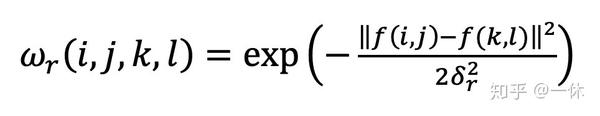
其中q(i,j)为模板窗口的其他系数的坐标，而f(i,j)表示图像在点a(i,j)处的像素值。p(k,l)为模板窗口的中心坐标点，对应的像素值为f(k,l);为高斯函数的标准差，值域核范围在[0,1]之间。
将上述公式2-12和2-13中的两个模板相乘就得到了双边滤波器的模板权值：
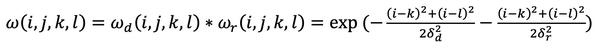
化简的双边滤波器的数据公式可以表示为：
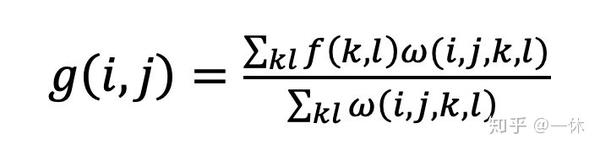
从以上公式可知，双边滤波是综合了高斯滤波和α-截尾均值滤波器的特点，同时考虑了空间域与值域的差别，而高斯滤波和α均值滤波分别只考虑了空间域和值域差别。高斯滤波器只考虑像素间的欧式距离，其使用的模板系数随着和窗口中心的距离增大而减小；α-截尾均值滤波器则只考虑了像素灰度值之间的差值，去掉像素灰度值的最小值和最大值后再计算均值。
空域权重衡量的是p,q两点之间的距离，距离越远权重越低。而值域权重
衡量的是p,q两点之间的像素值相似程度，越相似权重越大。在图像上直观的理解就是，当图像处于没有边缘跳变的平坦区域，临近像素的像素值得差值较小，对应的值域w_r就比较小接近于1，此时的空域权重
起主要作用，相当于直接对该区域进行高斯滤波。因此，在平坦区域相当于高斯滤波。在有边缘的区域，相临近的像素的差值较大，对应的值域权重
就接近于0，导致此处函数下降，即双边滤波的模板权值 w就接近于0。当前像素受到的影响就越小，从而保持了原始图像的边缘细节信息。
这里使用opencv中的bilateralFilter(src=image, d=0, sigmaColor=100, sigmaSpace=15)函数实现图像双边滤波，参数src表示的是图像的输入图像；d是过滤时周围每个像素图像领域的直径；sigmaColor是颜色空间过滤器的sigma值(对应上式，参数越大，会有越远的像素被混合到一起；sigmaSpace是坐标空间滤波器的sigma值(对应上式
，参数越大，那些颜色足够相近的的颜色的影响越大。总体的代码如下：
#双边滤波
bilateral_filter_img1 = cv2.bilateralFilter(img, 9, 75, 75)
bilateral_filter_img2 = cv2.bilateralFilter(gasuss_noise_img, 9, 75, 75)
#显示
plt.figure(figsize=(15, 15))
plt.subplot(3, 2, 1), plt.imshow(img)
plt.axis('off'); plt.title('原图')
plt.subplot(3, 2, 2), plt.imshow(gasuss_noise_img)
plt.axis('off'); plt.title('添加随机高斯噪声')
plt.subplot(3, 2, 3), plt.imshow(bilateral_filter_img1)
plt.axis('off'); plt.title('原图双边滤波')
plt.subplot(3, 2, 4), plt.imshow(bilateral_filter_img2)
plt.axis('off'); plt.title('加噪声后双边滤波')
plt.subplot(3, 2, 5), plt.imshow(gasuss_filter_img2)
plt.axis('off'); plt.title('原图高斯滤波')
plt.show()
运行上述代码可得下图所示的结果图，对比第三张图片和其它图片，可以发现双边滤波有很好的祛斑磨皮效果，通过调整代码中的两个sigma参数和半径d可以进一步优化表现。
链接：https://zhuanlan.zhihu.com/p/118496347
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
高斯滤波，本文主要讲其如何通过C语言实现。不太擅长写理论性质的文章，这里仅仅阐述自己怎么实现以及简单的优化过程。
通常我们对获取的图像进行进一步处理时，往往需要先进行一次降噪，而通常我们选择的是高斯滤波也称高斯模糊，其因为较好的降噪效果而被广泛使用，具体的原因大家可以做实验以及看相关的论文去理解。
如果你经常使用MATLAB或者Python，可能只需要调用一下库函数即可实现。以matlab为例，其高斯滤波的常见使用，如下：
% Generate Kernel[5, 5], sigma = 1.0.
gaussKernel = fspecial('gaussian', [5, 5], 1.0);
% Compute gaussian filter result.
gaussResult = imfilter(Image, gaussKernel, 'replicate');真的是方便至极，但自己不实现一下，好像没什么意思。并且嵌入式设备没有相应的库函数让你使用，所有还是有必要对其进行理解和学习。以下为正文分割线。
理论公式与模板生成
高斯滤波作为一种线性滤波器，其本质是带权值的加权均值滤波，相对于均值滤波，高斯滤波除了中心位置为1，其他位置根据距离的远近，越远滤波系数权重越低。
对高斯滤波的公式进行理解学习，参考如下公式：
其中， 为模板中心坐标，即坐标系原点。有了该公式，我们就可以实现高斯模板的生成了，参考如下
C代码：
void kernelGenerate(float *gaussKernel, int k_size, float k_sigma) {
float flag = 1 / (2 * PI * k_sigma * k_sigma);
float coef;
float sum = 0;
int center = (k_size - 1) / 2;
for (int i = 0; i < k_size; i++) {
float x2 = (float)pow((i - center), 2);
for (int j = 0; j < k_size; j++) {
float y2 = (float)pow((j - center), 2);
coef = (-x2 - y2) * flag;
gaussKernel[i * k_size + j] = flag * exp(coef);
sum += gaussKernel[i * k_size + j];
}
}
/* Normalize */
if (sum) {
for (int i = 0; i < k_size * k_size; i++) {
gaussKernel[i] /= sum;
}
}
}这个模板是生成的小数模板，要是生成整数模板呢？如下，将左上角置1。然后再进行取整操作。
void kernelGenerate(float *gaussKernel, int k_size, float k_sigma) {
float flag = 1 / (2 * PI * k_sigma * k_sigma);
float coef;
int center = (k_size - 1) / 2;
for (int i = 0; i < k_size; i++) {
float x2 = (float)pow((i - center), 2);
for (int j = 0; j < k_size; j++) {
float y2 = (float)pow((j - center), 2);
coef = (-x2 - y2) * flag;
gaussKernel[i * k_size + j] = flag * exp(coef);
}
}
/* Intergel Normalize */
if (gaussKernel[0]) {
float normal = 1.0 / gaussKernel[0];
for (int i = 0; i < k_size * k_size; i++) {
gaussKernel[i] *= normal;
}
}
}有了模板之后，就需要进行滤波了。通过公式，可以发现滤波最关键的就是滤波的核的标准差，因此需要根据实际的需要对其进行相应的设置。
滤波处理
如果直接使用公式，进行滤波则可以写出如下代码：
void gaussian_filter(unsigned char *src, unsigned char *dst, int src_w, int src_h, int k_size, float k_sigma, int padd_type, int out_type) {
int img_w, img_h;
if (k_size == 1)
dst = src;
if (k_size % 2 == 0) {
printf("The kernel size not odd and ksize > 1! Convert it to k_size + 1");
k_size += 1;
}
int padd_size = (k_size - 1) / 2;
img_w = src_w + padd_size * 2;
img_h = src_h + padd_size * 2;
unsigned char *pBlur = (unsigned char *)malloc(img_w * img_h);
unsigned char *pDst = dst;
float *gaussKernel = (float *)malloc(sizeof(float) * k_size * k_size);
for (int i = 0; i < src_h; i++) {
unsigned char *pTmp = pBlur + (padd_size + i)* img_w + padd_size;
memcpy(pTmp, src + i * src_w, src_w);
/* col padding */
for (int j = 0; j < padd_size; j++) {
if (padd_type == 0) { // zero padding.
pTmp[j - padd_size] = 0;
pTmp[src_w + j] = 0;
} else { // reflect padding.
pTmp[j - padd_size] = pTmp[padd_size - j];
pTmp[src_w +