高斯投影,高斯-克吕格投影、UTM投影
百度Apollo|无人驾驶|图解传感器地球之间的坐标关系以及如何转换 - 知乎 (zhihu.com)
动画说明高斯投影:
工程测量:3_1-3高斯投影 - 【工程测量】 - 西瓜视频 (ixigua.com)



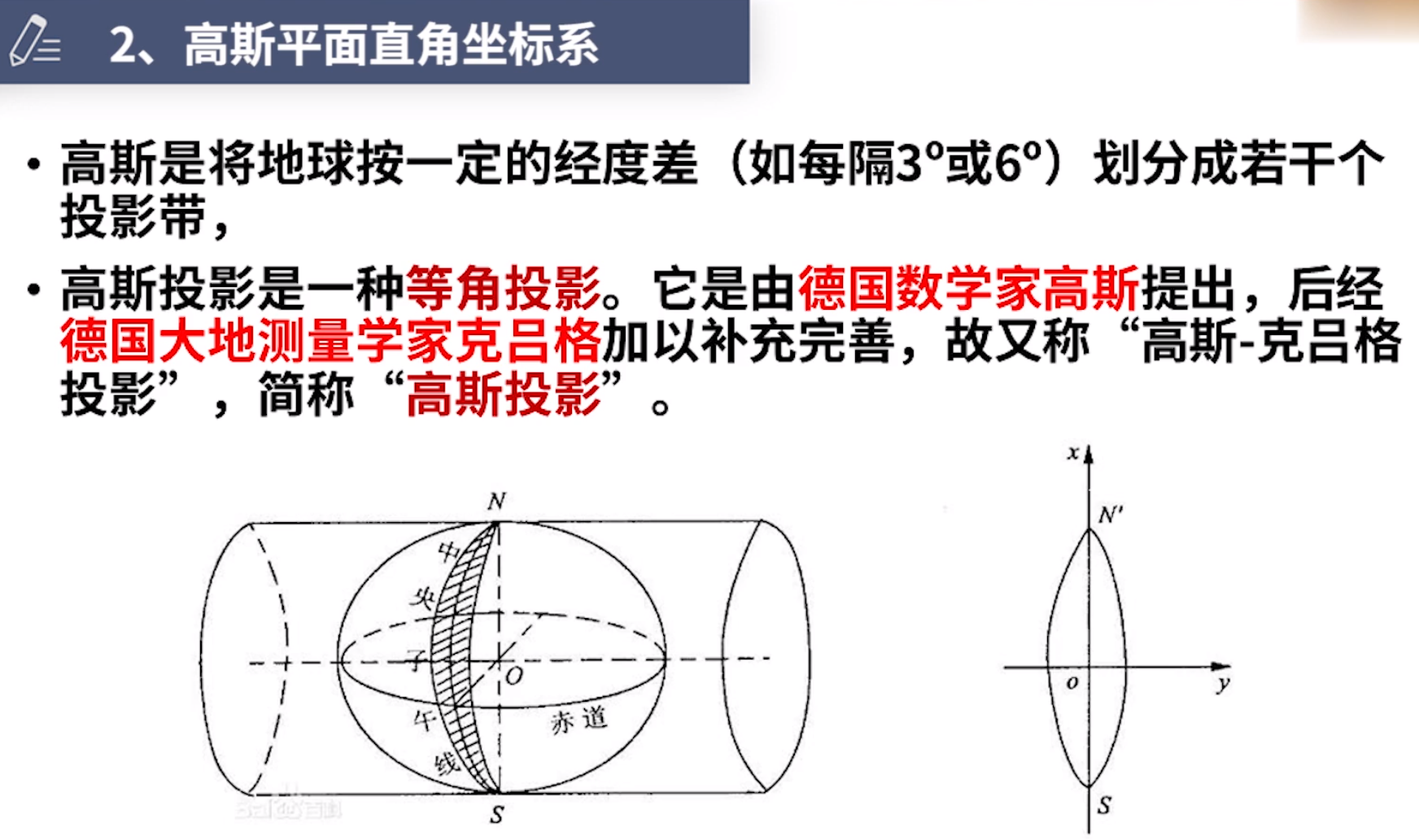



测绘基础视频教程1高斯投影 - 西瓜视频 (ixigua.com)

(202) UTM投影 | 高斯克吕格投影 | UTM Projection | Gauss-Kruger Projection | 变形系数 | Scale Factor - YouTube
小结:
1.高斯投影是等角正轴切椭圆柱投影。
2.UTM(universal tranverse mercator)是的等角横轴割椭圆柱投影。
投影
在地球椭球面和平面之间建立点与点之间函数关系的数学方法,称为地图投影。
高斯克里格投影
像拨开的橘子瓣,我国大中比例尺地图均采用这种投影。
高斯-克吕格投影分带规定
该投影是国家基本比例尺地形图的数学基础,为控制变形,采用分带投影的方法,在比例尺1:2.5万—1:50万图上采用6°分带,对比例尺为1:1万及大于1:1万的图采用3°分带。
6°分带法:从格林威治零度经线起,每6°分为一个投影带,全球共分为60个投影带,东半球从东经0°—6°为第一带,中央经线为3°,依此类推,投影带号为1—30。其投影代号n和中央经线经度L0的计算公式为:L0=(6n—3)°;西半球投影带从180°回算到0°,编号为31—60,投影代号n和中央经线经度L0的计算公式为L0=360—(6n—3)°。
问:东半球和西半球的划分依据是什么?
答1:格林威治天文台的0度经线。
答2:东西半球的划分是按照经线圈来划分的,但是这里有一个误区,有人认为东半球就是经度是东经的区域,西半球就是经度是西经的区域,也就是从0°经线往东至180°经线是东半球。其实不对,现实当中的东西半球不是这样划分的,由于0°经线刚好经过了英国伦敦的格林威治天文台,所以如果以0°经线作为东西半球的分界,那么英国等国家就会分属不同半球,为此实际上东西半球是以主要经过海洋的经线西经20°和东经160°为界划分的,也就是西经20°往东至160°为东半球。
3°分带法:从东经1°30′起,每3°为一带,将全球划分为120个投影带,东经1°30′—4°30′,…178°30′—西经178°30′,…1°30′—东经1°30′。
东半球有60个投影带,编号1—60,各带中央经线计算公式:L0=3n,中央经线为3°、6°…180°。西半球有60个投影带,编号1—60,各带中央经线计算公式:L0=360°—3°n,中央经线为西经177°、…3°、0°。
为了便于地形图的测量作业,在高斯-克吕格投影带内布置了平面直角坐标系统,具体方法是,规定中央经线为X轴,赤道为Y轴,中央经线与赤道交点为坐标原点,x值在北半球为正,南半球为负,y值在中央经线以东为正,中央经线以西为负。由于我国疆域均在北半球,x值均为正值,为了避免y值出现负值,规定各投影带的坐标纵轴均西移500km,中央经线上原横坐标值由0变为500km。为了方便带间点位的区分,可以在每个点位横坐标y值的百千米位数前加上所在带号。
高斯-克吕格投影特点
1、中央子午线是直线,其长度投影前后不变形;其他子午线是凹向中央子午线的弧线,并以中央子午线为对称轴;
2、赤道线是直线,但有长度变形;其他纬线为凸向赤道的弧线,并以赤道为对称轴;
3、经线和纬线投影后仍然保持正交;
4、离开中央子午线越远,变形越大;
5、投影前后角度不变,投影后经线和纬线仍然垂直。
l:经差
B:纬度
N:法线长(法线位于椭球面和短轴之间的长度)

%======================================================================%
2021.9.13
%======================================================================%
参考:




注:
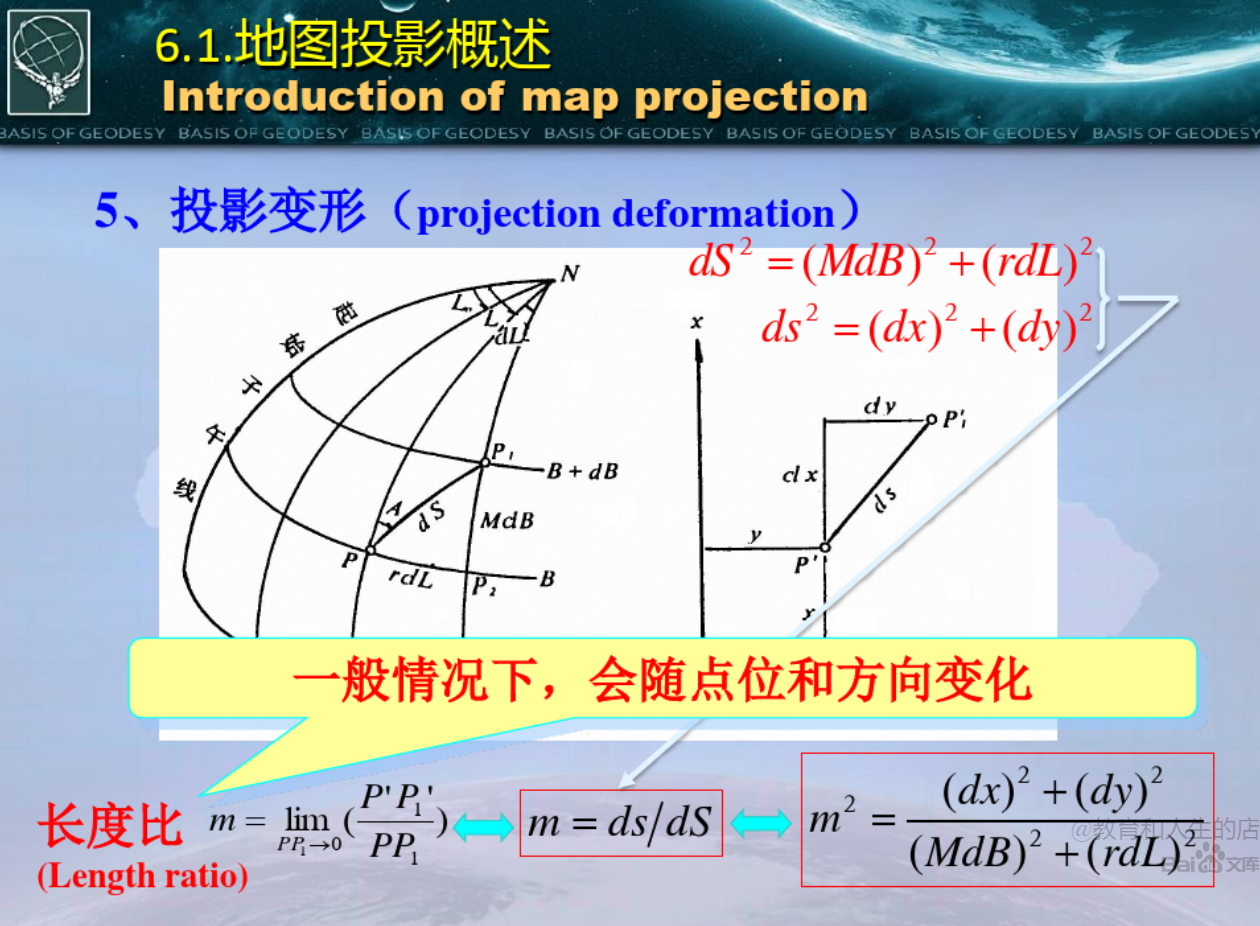
1.长度比是投影后的长度和投影之前的长度的比值,也就是投影后的一段弧素比上投影前的一段弧素。
2.长度比是一个取极限的值。
3.ds和dS分别是椭球面上和平面上的一段弧素。
注:
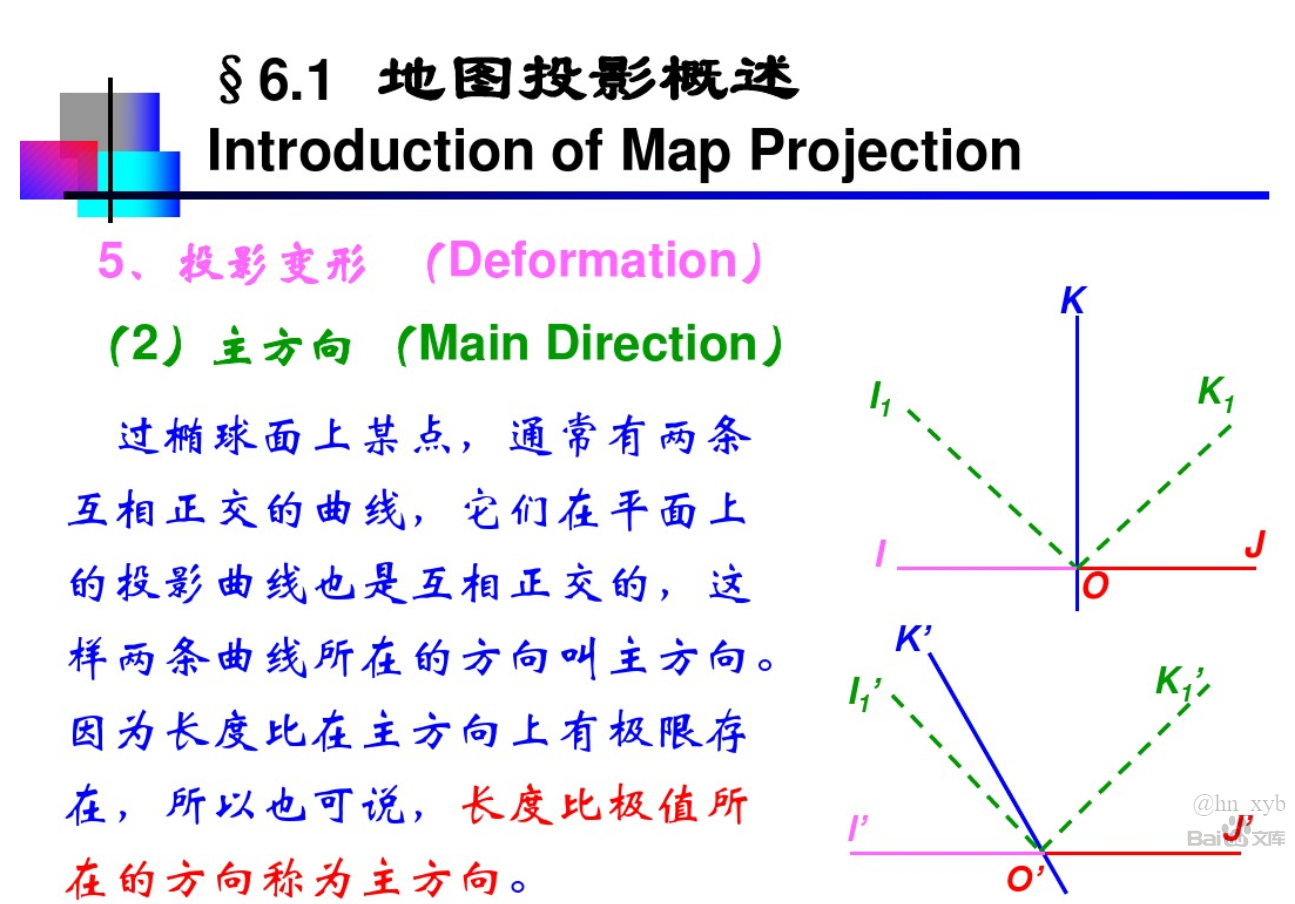
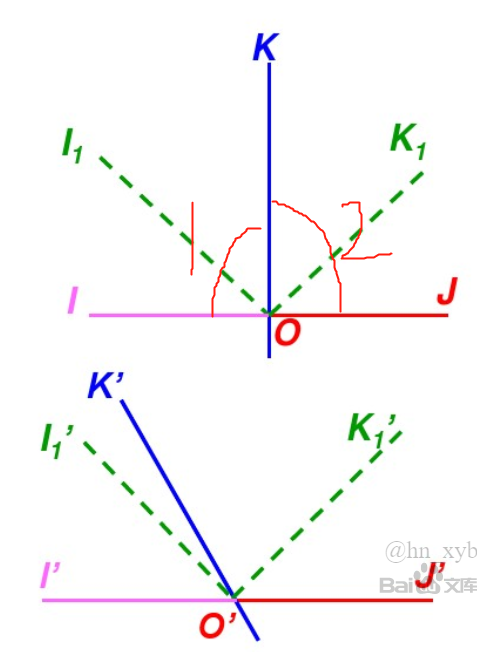
1.右上图是椭球上的图像,右下图是投影到平面上的图像。可以看到曲线OK发生了变形,方向变化了。
2.投影前后,IOK直角和JOK直角分别变成了锐角I'O'K'和钝角J'O'K'.
3.从椭球面到平面的投影结果是角1投影变成了锐角,角2投影变成了钝角,直角1顺时针旋转到角度2的过程中,中间一定有一个瞬间,是投影之后仍然保持直角的,如图绿色所示。
4.简单来说,椭球面上的正交的曲线在投影到平面上之后还能保持正交的话,那这两条曲线所在的方向就叫主方向。


1.研究发现,在主方向上,长度比往往存在着极值。
2.两个长度比的极值中的两个长度比是指主方向上的两个长度比。

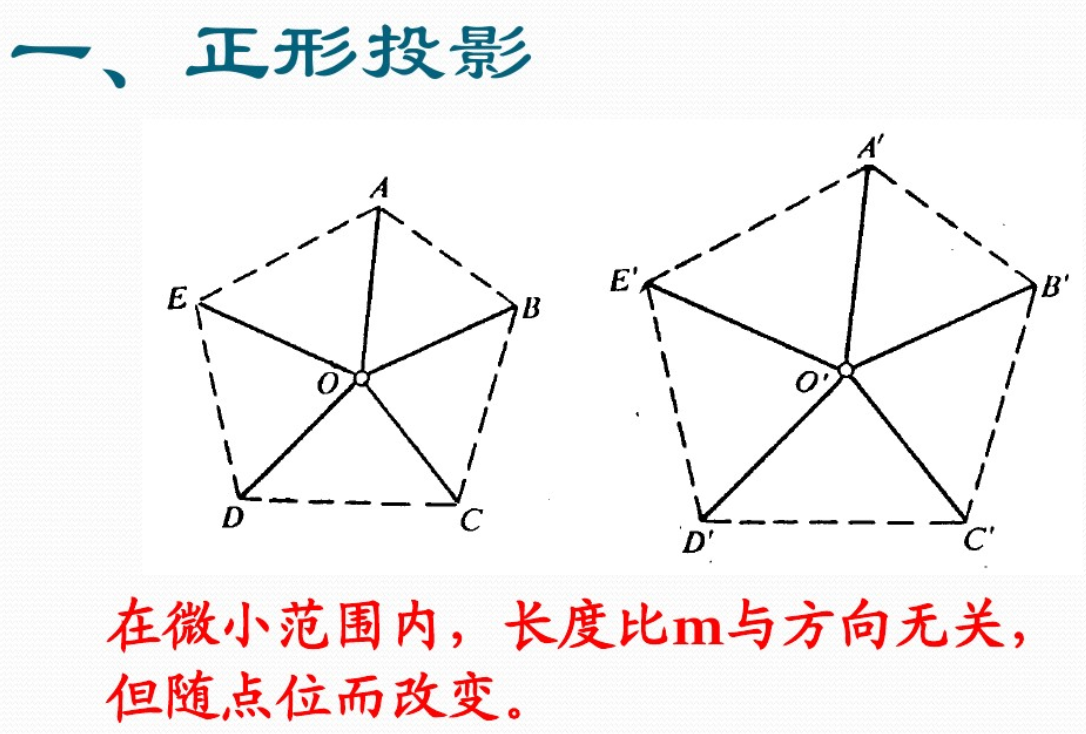





注:
平面投影是不涉及到高程的。

%======================================================================%
2021.9.14 高斯投影和高斯平面直角坐标系
%======================================================================%
参考:
https://www.bilibili.com/video/BV1na4y1s7NX?p=30
本节主要讲的是高斯投影和高斯平面直角坐标系。
大地空间直角坐标和大地坐标之间的转换:
![]()
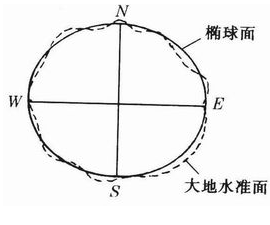
大地坐标和天文坐标之间的转换:
![]()
H大代表的是椭球面中的大地高。
A代表大地方位角,注意是大地方位角,不是大地坐标方位角,大地方位角和坐标方位角是两个概念。
右边四个字符表示:天文经度,天文纬度,正高,天文方位角。
天文测量的高程是以大地水准面为基准面的,测出来的高程称为正高。
L,B和lamna,fai之间的公式是垂线偏差公式。
A和α之间的公式是拉普拉斯方位角公式。
大地极坐标和大地坐标之间的转换关系:
![]()
今天的内容是椭球面大地坐标和平面直角坐标之间的转换关系:
![]()
地面测量元素归算到椭球面上:
![]()
方向归算加了三差改正。
距离:斜距归算。
方位:把α归算成A。
今天的任务是继续把椭球面的元素归算到(高斯)平面上。

通过观测量计算坐标的流程图:
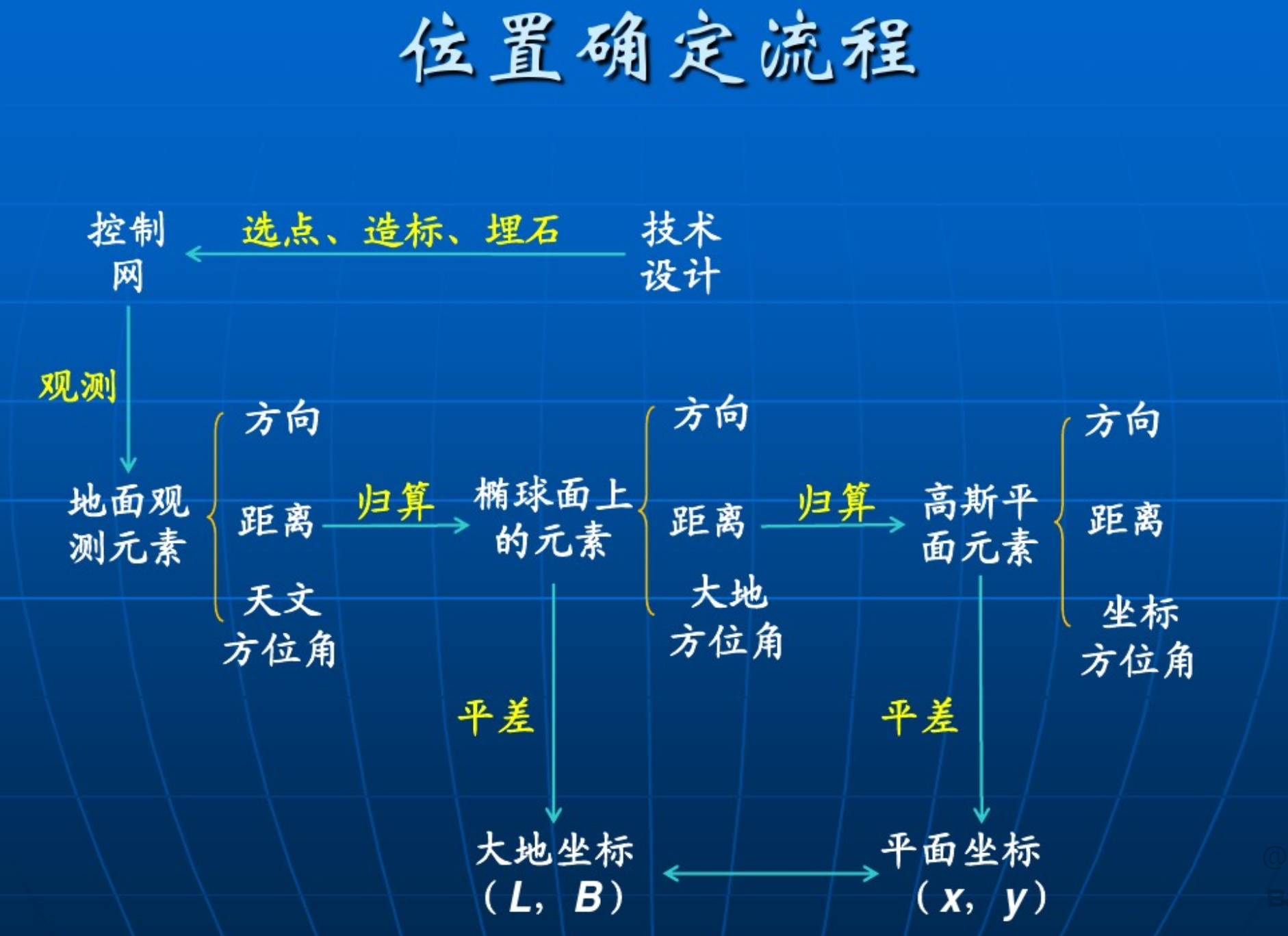
有边和角怎样推算坐标?这个是大地问题正解。根据多余观测进行平差,求取大地坐标。但是现在有了GPS了,直接测出来的就是大地坐标了,所以这个过程不用人为计算了。但是理论不会过时。比如,测量控制是根据大地坐标反算地面上的方向、椭球面上的距离和地面上的距离。

注:
平差模型涉及到最小二乘平差的方法。
问题1:为什么要投影?
问题2:什么是投影?
问题3:怎样投影?
问题1的解答:
椭球上建立的坐标系不能用于测图,因为测出来的图是以图纸的形式展现的,是二维的。

控制测图的第一件事情就是建立大地控制,画了很多的方里网,实际上是为了控制这个区,使得每个测区的误差都限制在1Km范围之内。
%======================================================================%
2021.9.17 高斯投影和高斯平面直角坐标系
【大地测量学基础】解放军信息工程大学丨含课件_哔哩哔哩_bilibili
%======================================================================%
控制测图的第一件事情就是建立大地控制,画了很多的方里网,实际上是为了控制这个区,使得每个测区的误差都限制在1Km范围之内。然后在这个基础上,再把公路,桥梁,山脉,水系等地图要素叠加上去。
但这是平面,地球小范围内可以作为平面,但大范围内就不可以了。投影就是解决椭球面到平面投影时候的变形问题。实际上是把变形这个误差平均的分配掉,使得在任意一个图幅内,这种变形误差都小到可以忽略掉的程度。这就是要投影最主要的原因。
简单来说,第一个原因是测图需要做控制,控制的话需要平面上的坐标。椭球上的大地坐标不能直接用作控制测图。
第二个是第一个原因带来的副产品,就是投影之后,在平面上做各种计算会变得简单。椭球面上算坐标要用白塞尔公式,很复杂的。如果这个问题放在平面上,会非常的简单。
什么是投影?

投影就是建立一种数学模型。

投影的方法:
1.几何法:比如通过光线的方式把电影由投影机放大到屏幕上,这个是一种几何投影;
2.椭球面到曲面的投影是一种解析投影,是通过一种数学关系做的投影,跟方法1不是一回事。严格的说,这种数学关系的投影是没有几何意义的。


大地线是什么样子的线呢?待解答。。。

圆柱面依据其母线展开成平面不会有任何变形的,具体的说就是,圆柱面上的图形不会有任何变形的。这样的曲面叫可展曲面。
三维的圆锥面也是可展曲面。
但球面、椭球面不是可展曲面。如果强制展开,会出现褶皱,破裂。必然会出现变形的问题。

通过调整函数模型,来合理的分配变形引起的误差。使得变形符合我们的应用需求。

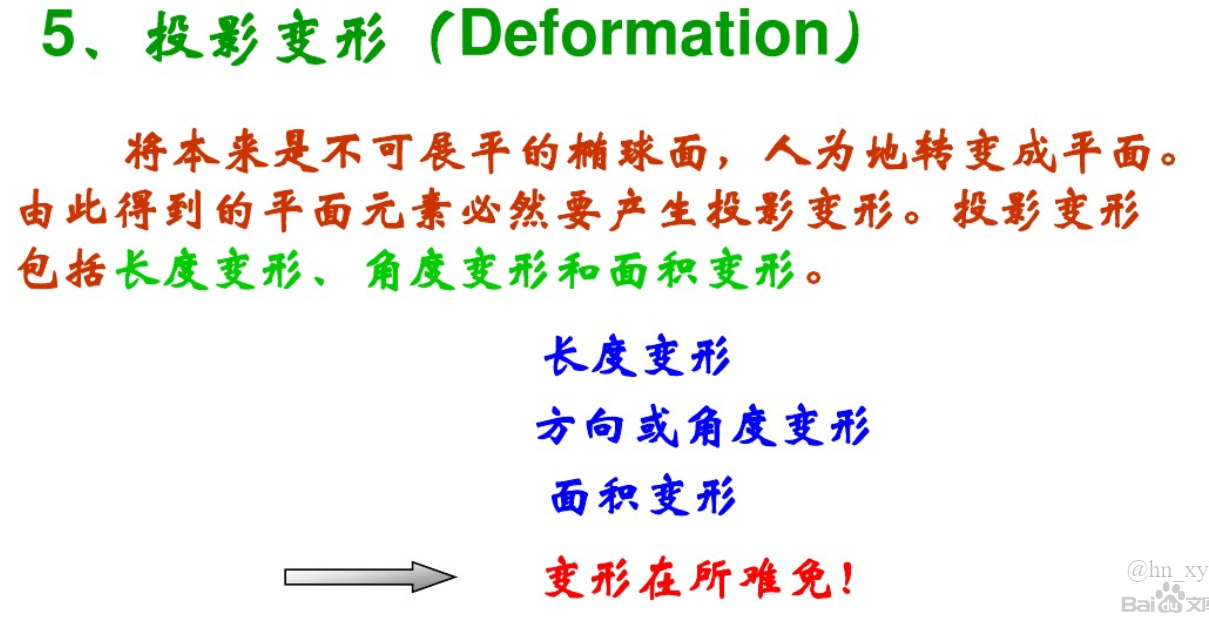
四类变形:
航海的话,希望投影到图纸上,方向不要有变换。土地管理的话,希望投影到图纸上,面积不要有变化,大地测量中,希望是等角的投影,因为等角投影就意味着图形投影前后是相似的。军事上也比较适合等角投影,因为可以在相似的图形上排兵布阵。
下面的问题就是:建立投影前后的数学模型,或者说函数关系,建立的数学模型要保证角度在投影前后保持不变。即椭球面上的角度是多少度,投影到平面上之后,还是多少度。一个90°的角投影到平面上之后还是90°。就是说建立的模型中要包含等角这个性质。


先找到一个和等角性质等价的一个数学性质,这就是:正形特性。
m叫做长度比。

A:大地方位角。
![]()
![]()
大地方位角的解释来自:大地方位角 - 《中国大百科全书》第三版网络版 (zgbk.com)
dS是椭球面上的微分线段(椭球面上的大地线弧素),ds是平面上的微分线段,微分状况下的曲线可以认为是直线。投影后平面上的微分线段与投影前椭球面上的微分线段的比值称为长度比。
正形特性是说:长度比与方向无关。
下面证明这个正形特性:

看上图:da是椭球面上A点任意一个方向的一段大地线弧素,db是另外一个方向的大地线弧素,现在正形特性是说,图中红色方框处可以画个“=”号。
分别在椭球面上和平面上作一个辅助线,分别构成两个三角形,为何要构成三角形?答:可以 利用到三角形的相似性。

我们的已知条件是我们要求投影前后角度保持不变,所以要构建三角形,这样可以充分的利用已知条件。把已知条件包含进推到的过程。
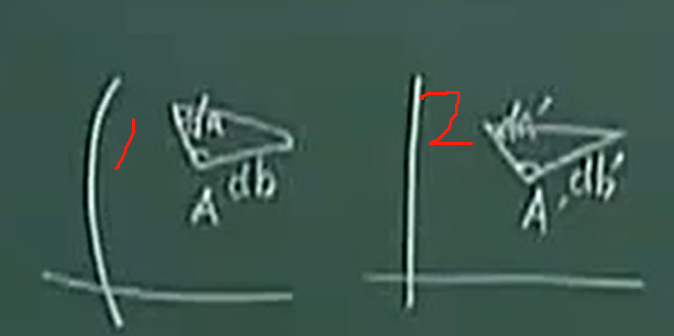
小范围内,图形1和2都可以看成是三角形。1中的球面三角形可以看成是平面三角形(小范围内),2中的曲线可以看成是直线(小范围内)。因为前提要求等角特性,所以这两个三角形形似,可得出,它们对应的边成比例。既然相似,那可以画等号。
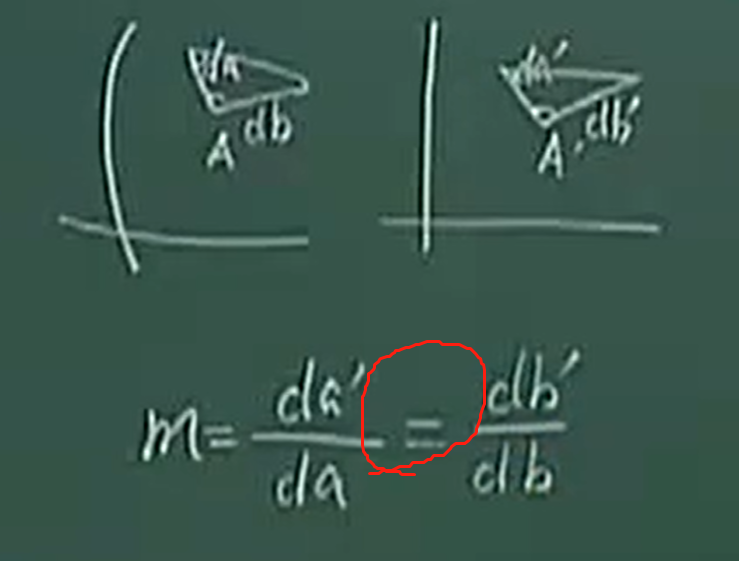
下面再任取一个方向,可以很自然的得出下图中的等式:

长度比和方向无关相当于是等角的另外一个表示方法。


反证法证明方框中的不等式:B点是任意取的,假如mA=mB,那么就说明投影前后没有变形了,这个应该是圆柱面或者圆锥面了,而事实上,椭球面投影前后,变形不可以避免,所以,mA=mB,一定不成立。

这个比值跟方向应该是没有关系的。
引入A的目的是为了消去A。


下面通过m的表达式引入大地方位角。
dS是子午圈弧素,ds是平行圈弧素。
问:平行圈(纬度圈)弧长公式:
答:

注:
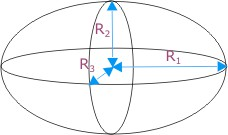
1.纬度圆半径r=NcosB,是纬度的函数。N是法线长。N=a/w=c/v 是跟椭球有关的一个常数,椭球确定了,N也就确定了。
关于a和w,c、v的说明见下面2图:


问:子午圈(子午线)弧长公式?
答:

注:
1.M是子午圈曲率半径。
M=a(1-e2)/w3,也是纬度的函数。w=sqrt(1-e2sin2B).子午圈曲率半径与纬度成正比,赤道处最小,等于椭球长半轴,往两极逐渐增大,到极点处无限大。
因为M/r是纬度的函数,所以M*dB/r可以看作是某个函数的微分:

下面这个积分完全取决于大地纬度,大地纬度已知了,q也就知道了。

给小q一个新的名字,叫做:等量纬度。
【大地测量学基础】解放军信息工程大学丨含课件_哔哩哔哩_bilibili
为何叫等量纬度,因为q是只是一个纬度的函数,就相当于q=f(B).B和q一一对应。
q和归化纬度不一样,q是没有几何意义的。归化纬度有几何意义,大地纬度也有几何意义,可以画个图看一下,q不行。这里的q的出现只是为了推导公式的方便。后面的高斯投影的推导和解算都只解算等量纬度就行了,因为q知道了,就意味着B也知道了。

椭球面上的就推到这里,下面看平面上的情况。
![]()
平面上的情况很简单:ds2=dx2+dy2,可以看下图。

注:
纵轴微分变化量是dx,横轴微分变化量是dy。
问:为何测量上的坐标轴和笛卡尔坐标系的坐标轴不一样?
答:因为角度定义不一样,数学上的笛卡尔坐标系从x轴横轴逆时针方向定义的角度,而测量学上的角度是从纵坐标轴顺时针定义的方向。
在引入了等量纬度以后,
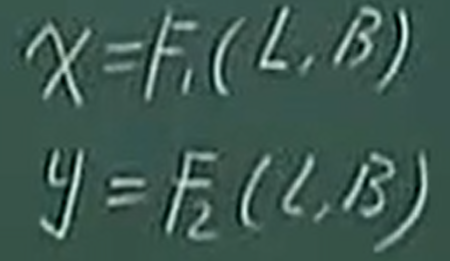
可以变成:
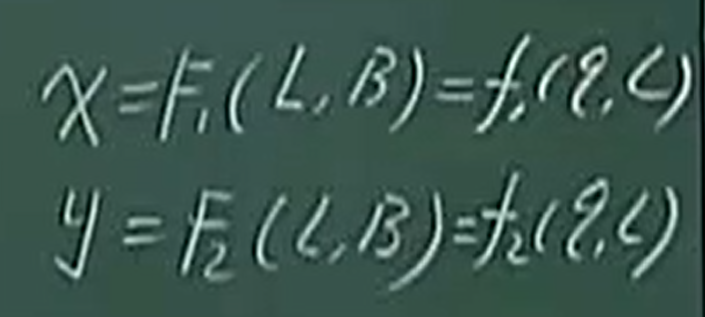
既然有这个表达式,ds2=dx2+dy2 (1),那么根据上图,我们就对x、y分别求全微分:
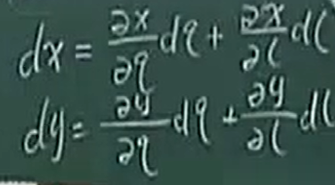
然后带入(1)式,如下:

下面是公式推导过程:

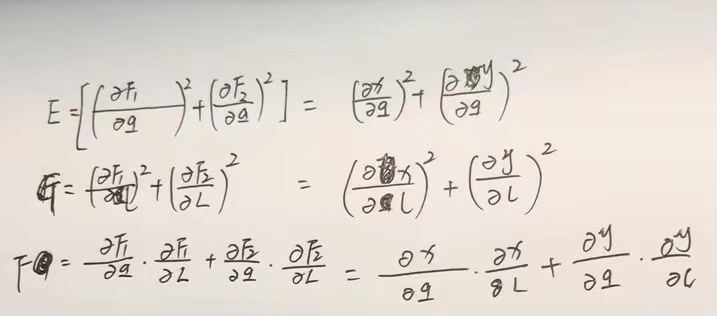

要始终记住任务:在m=ds/dS中,利用长度比和方向无关进行投影函数关系的推导。现在要看m的表达式中,有没有哪个量代表方向,或者说哪个量里面隐含有方向的信息。上图那些偏导数的值跟方向是没有关系的。偏导数相当于对坐标轴求偏导,dq、dl可以看成是两个坐标轴,偏导数的值只跟点有关系,跟方向是没有关系的,线段才跟方向有关系。
跟方向有关系的是什么量呢?
答:dq、dL。
这一段线段在两个坐标轴上的投影,是跟这一段线段的方向是有关系的。即跟A是有关系的。如下图中的dS这一线段:
dq、dL相当于是dS在两个坐标轴上的投影,方向不一样,投影长度自然不一样。所以跟A有关系的是dq、dL。

跟方向没有关系的看成是常数:E,F,G。
下面要做的事情是把A引进到dq,dL中。
因为是微分三角形,从上图中可以得出(分子分母同时除以r):
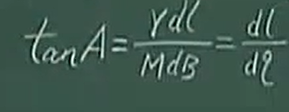
dl=tanA*dq,从而有:

下面是推导过程:

这样长度比m就显式的含大地方位角(方向)A了。椭球面到平面的投影的正形特性要求的是m与A无关。当上面化简出来的式子中,E=G,F=0的时候,m与A没有关系了。E=G=F=0也能满足m与A无关,此时m=0,这意味着ds=0,这时候地球投影到平面上之后,不是一个线段了,而是便成平面上的一个点了,这不是我们想要的结果。于是有:

幻灯片中应该是有一点小错误的,应改成:

解一下方程:
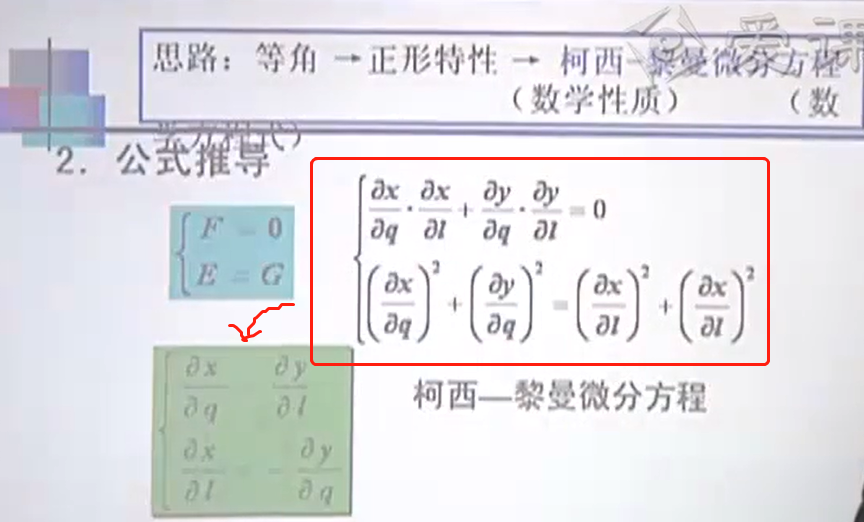

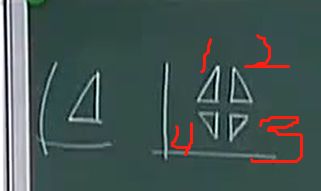
实际上,有1、2、3、4,共4组解(a/b/c/d的前面取正负对应这4组解),但是测绘上只取第1组解。即:投影前是东西方向的,投影后还保持东西方向,投影前是南北方向的,投影后还保持南北方向。
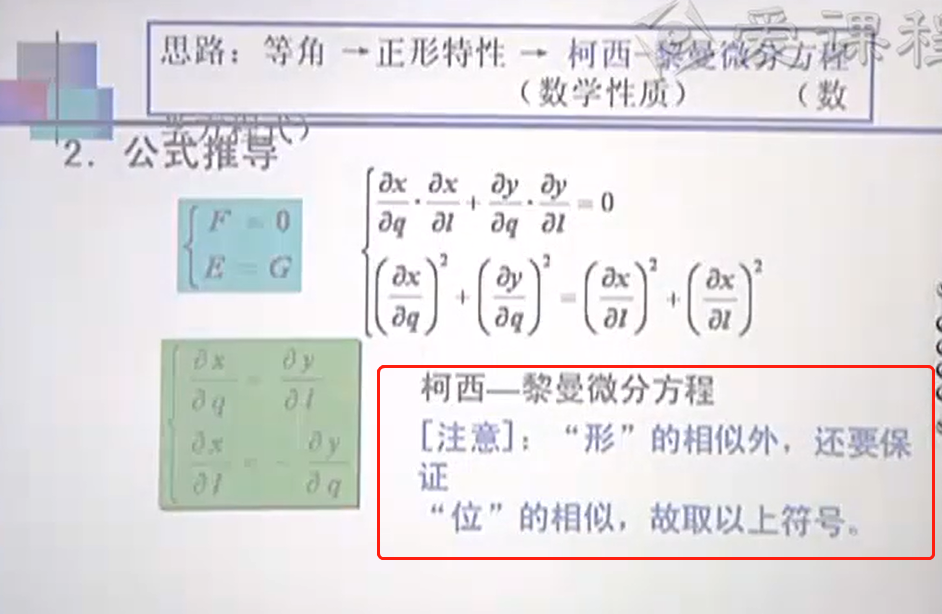
注:
"形"代表"形状"。
"位"代表"位置"。
一开始的问题是:根据投影前后的等角特性建立投影前后变量的函数关系式,----->下面建立x、y和q、l的关系,
这就是解上面这个微分方程。

另外,根据:

得到化简后的m:

这一节结束了,这一节的重点是推导代表椭球面到平面的正形(等角)投影条件,即:柯西-黎曼微分方程。
最终的目的还是要建立一种函数关系,关于椭球面到平面上的投影的函数关系。这个函数关系使得椭球面上的点和平面上的点一一对应。建立这种函数关系的时候,柯西黎曼微分方程是最基本的一个方程式,有了这个方程式,就可以求柯西黎曼偏微分方程的解了。
下一节开始:
【大地测量学基础】解放军信息工程大学丨含课件_哔哩哔哩_bilibili
前面建立的柯西黎曼微分方程是正形投影(等角投影)的一般的条件,解微分方程可以(也只能)得到一个通解,但要得到特解,还要加上一个积分常数,也就是说 ,要有附加条件的。
问:这个特解要附件的条件是什么呢?
答:高斯投影的特殊条件。
高斯投影就是在正形投影这个特征的前提下,再加上高斯投影的特殊的条件。特殊的两个条件,因为有两个偏微分方程,所以要附件两个特殊条件以求得两个积分常数。
可见,高斯投影是正形等角投影的一种,是正形投影加上两个特定条件的结果。
高斯投影的定义:

19世纪20年代相当于等角横切椭圆柱投影是高斯1825年左右提出的。克吕格对其进行完善是相当于差不多又过了87年之后的事情了。简称高斯投影好像对克吕格不太公平,个人认为应该简称为高-克投影。
上图中:x、y的表达式相当于是柯西黎曼微分方程的一个解。
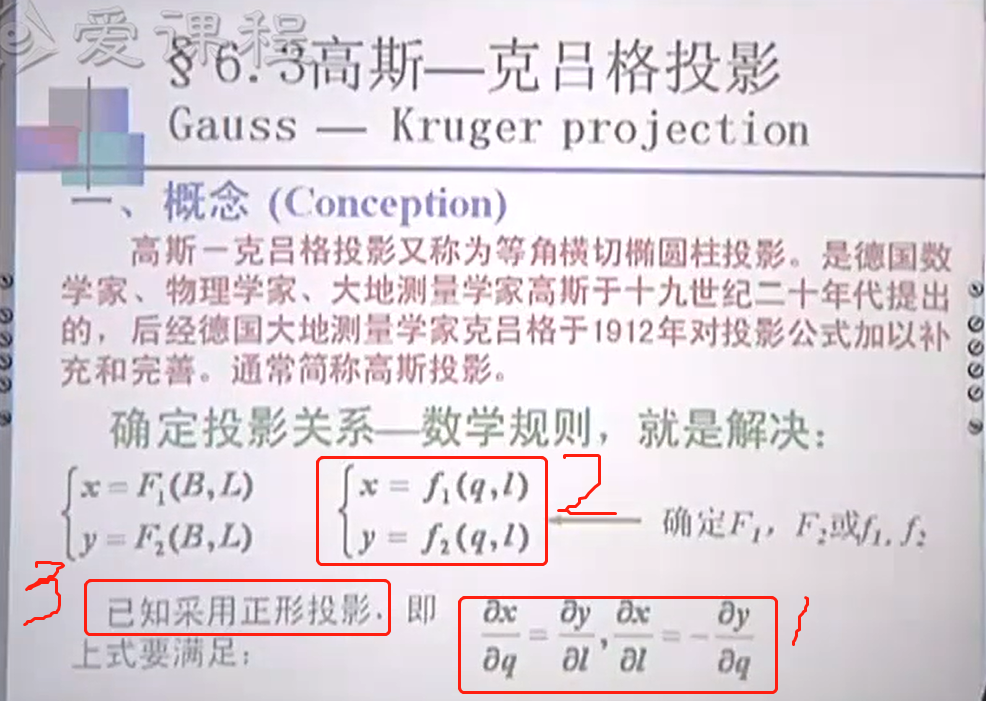
注:
1. 3是椭球面上的图形投影到平面上的一个要求;
2. 2是柯西黎曼偏微分方程1的一个解,这个解涉及到高斯投影的时候,要加2个积分常数变成特解,这两个积分常数由两个特殊条件确定。
两个特殊条件就是下图中的(2)和(3)。

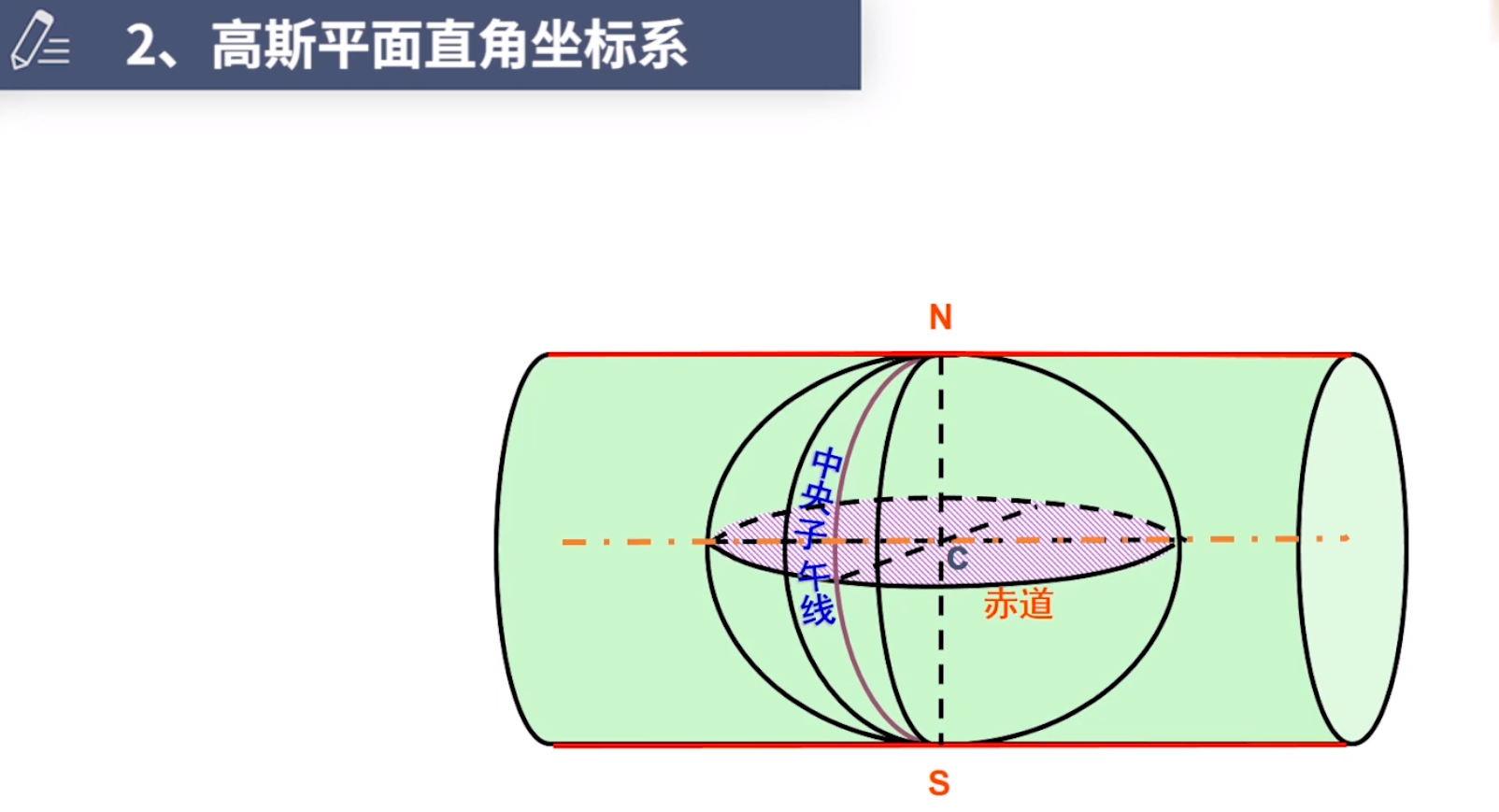
在投影的时候是取一个狭窄的地带投影。中央子午线的定义就是这个狭窄地带的中央经线。正形投影即角度保持不变的投影,角度保持不变的话,必然导致其他几何量的变化,比如长度,距离、面积等。带来的其他变形我们尽量限制它。限制变形的方法之一,就是小范围投影。目的就是保证等角,同时限制其他方面的变形。小范围的投影是一个花瓣的形状,位于经差中间值的那个子午线就叫做中央子午线。
下面的内容来自于:如何选择中央子午线或者分度带_哔哩哔哩_bilibili

注解:
1.图中:赤道下面的每一个“花瓣”都是3°,赤道上面的每一个“花瓣”都是6°。每个“花瓣”中央的线叫做中央子午线。相邻的6°带的中央子午线经度相差6°,相邻的3°带的中央子午线经度相差3°。
最东端 东经135度2分30秒 黑龙江和乌苏里江交汇处
最西端 东经73度40分 帕米尔高原乌兹别里山口(乌恰县)
最南端 北纬3度52分 南沙群岛曾母暗沙
最北端 北纬53度33分 漠河以北黑龙江主航道(漠河县)
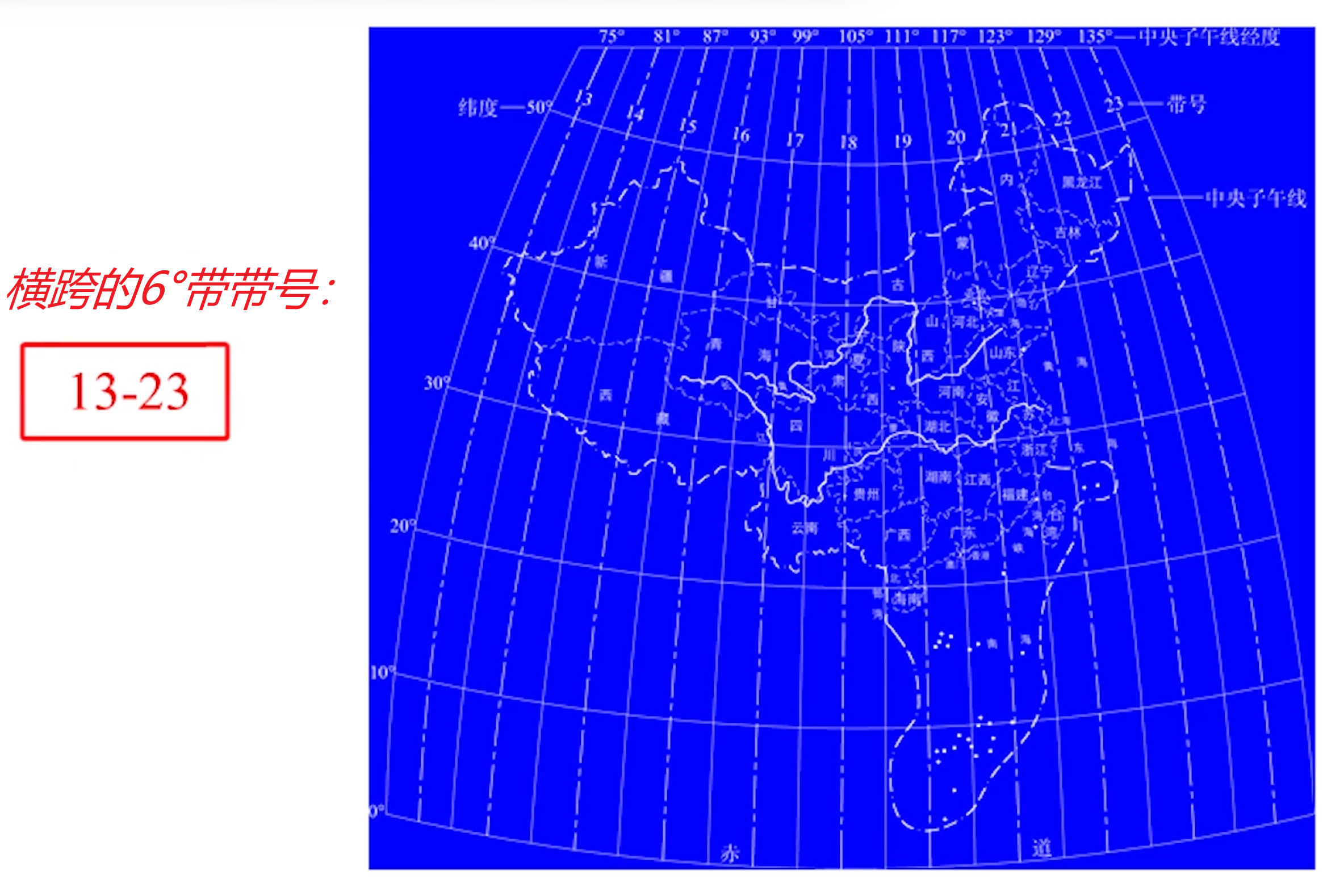
2.上图表示:因为我国横跨的经度大约是73°到135°,所以画高斯分带投影的时候,只需要画出我国的情况就行了。6°带分带的代号和3°带分带的代号也可以从上面图里面看出来。如果代号的范围小于23,则一定是6°带分带,如果代号的范围大于23,则一定是3°带分带。
中国版区所在的6°带范围:(0~60里面的)13~23
中国版区所在的3°带范围:(0~120里面的)25~45
3.图中的花瓣与花瓣之间的裂痕现实中是不存在的,现实中,每个花瓣都是单独的一个投影,这个图为了展示的方便,把所有花瓣画在了一起。
3.假如6°带分带的方法嫌变形大,或者子午线的长度变形无法满足工程上的需要,则重新选择中央子午线,或者在重新选择中央子午线之后,进行3°带的投影。

注:
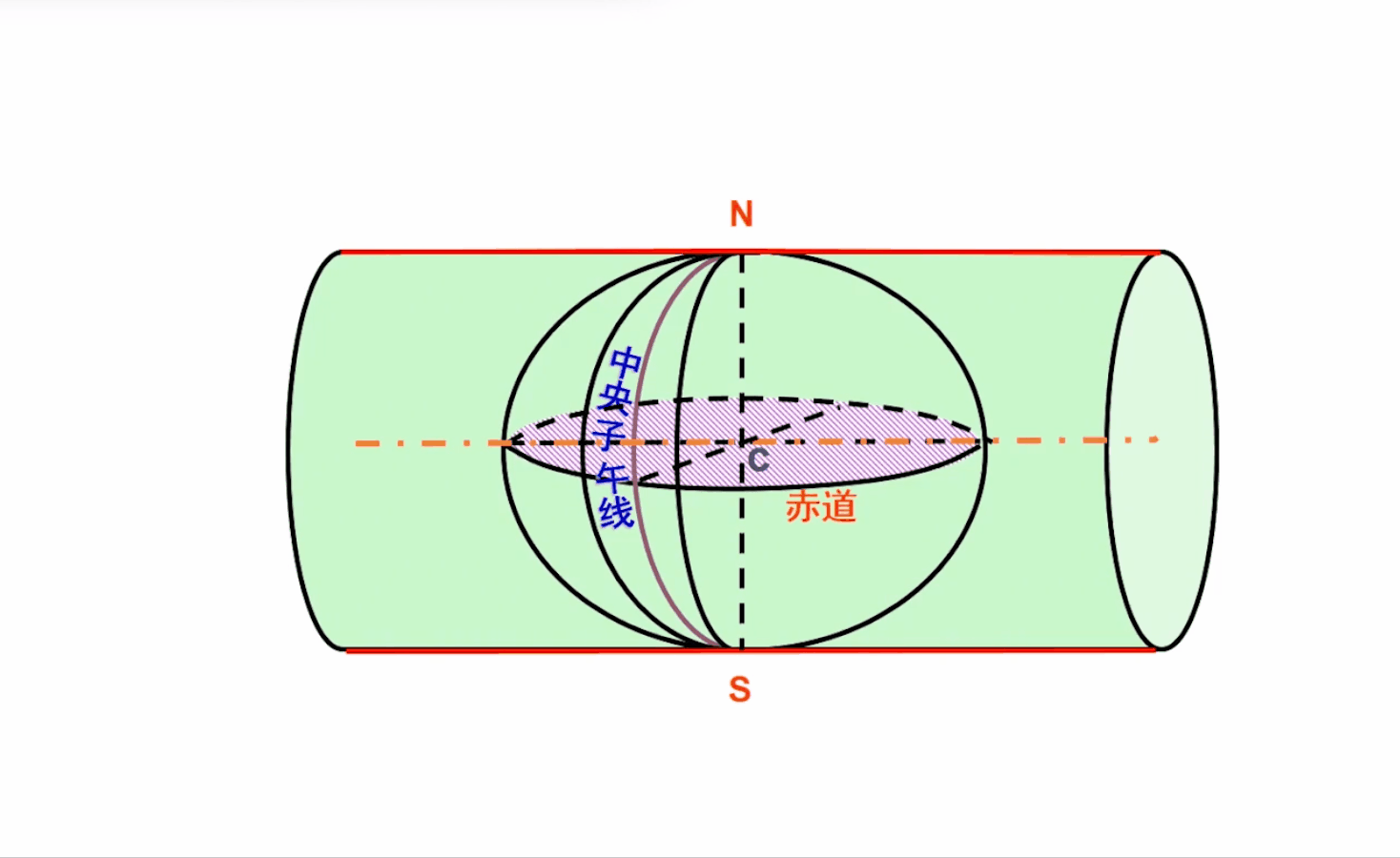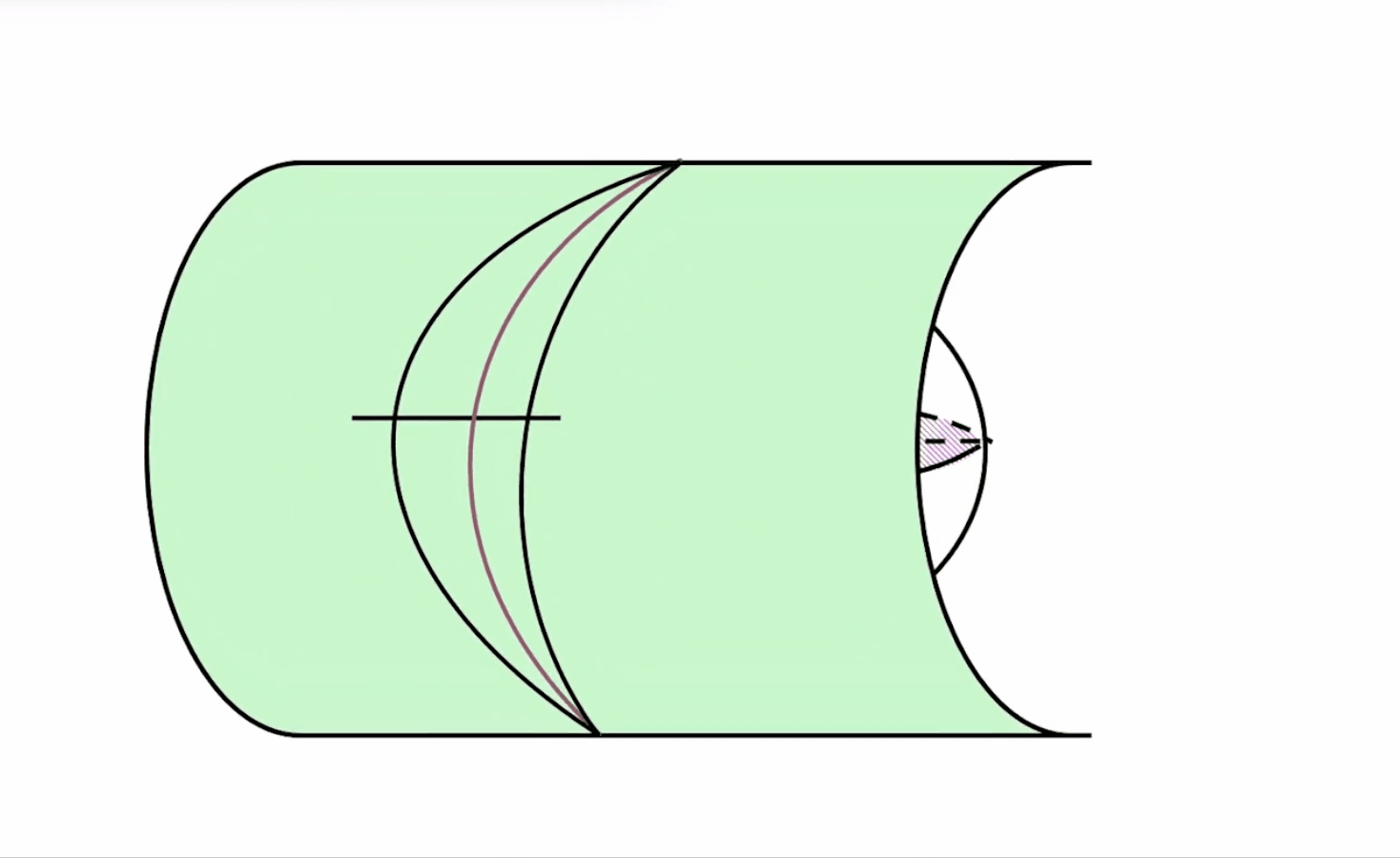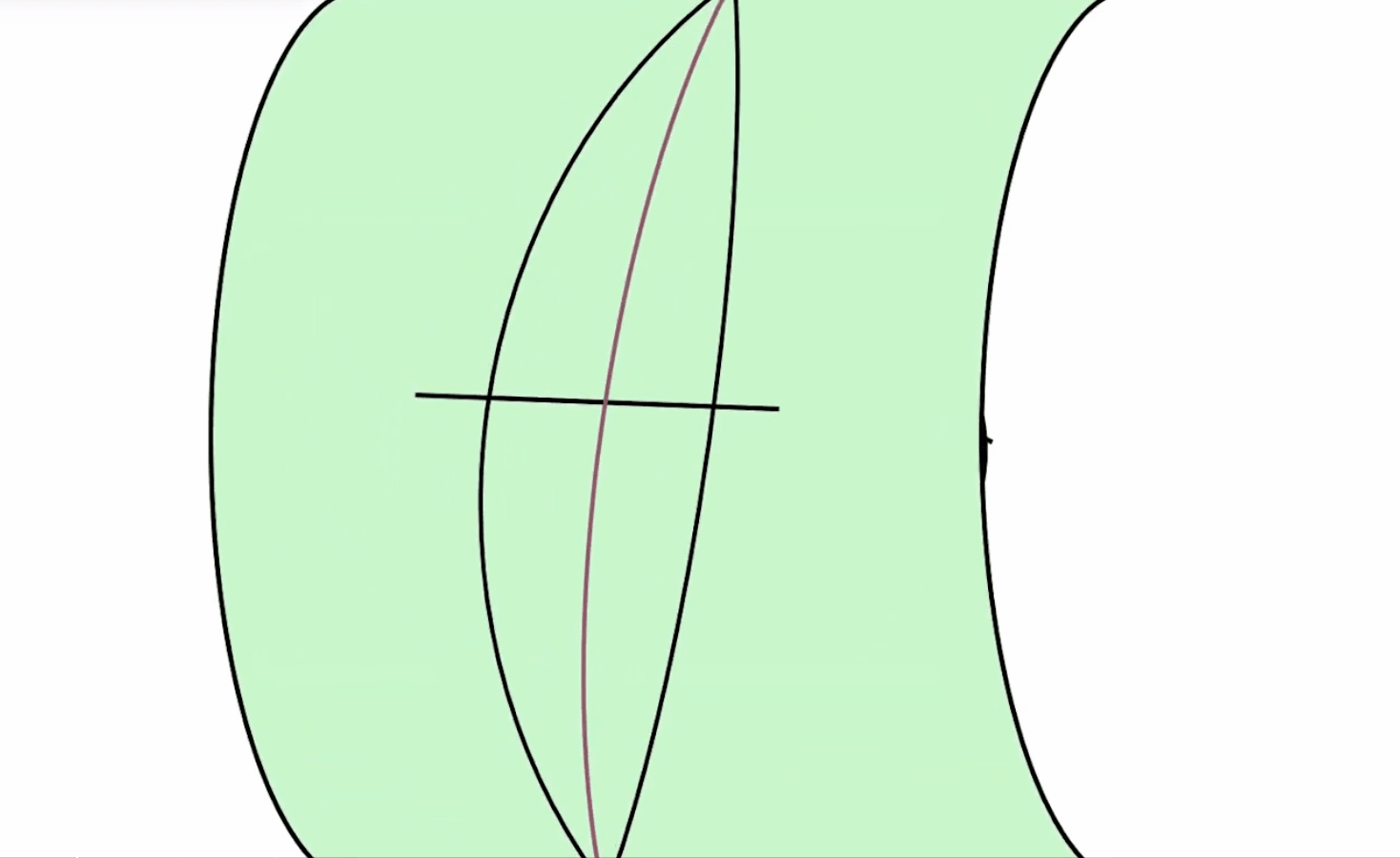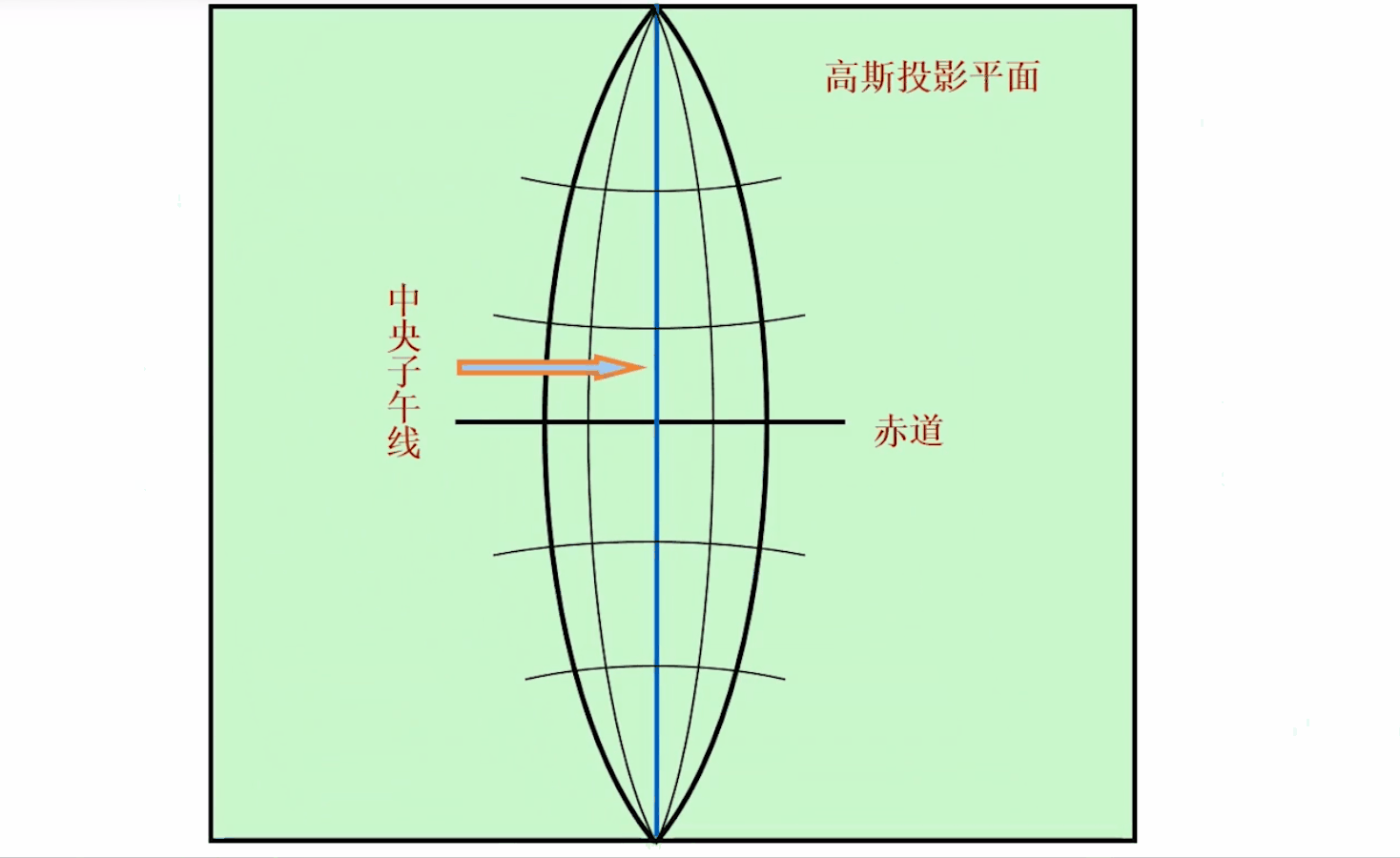
1.图中所示圆柱面是椭圆柱面。
2.一开始说高斯投影不是几何投影,现在怎么可以用几何图像展示了?答:只是近似的可视化表达。
3.椭圆柱面和哪条子午线相切,那条子午线就叫做中央子午线。

注:
1.相切处的中央子午线是因为紧贴着椭圆柱面,是不透光的,所以椭圆柱面沿上下两条母线剪开时,中央子午线长度不会变。子午线弧长自然也不会变,即有:x=X.
2.中央子午线旁边的子午线叫做分带子午线。
3.在椭球面上,中央子午线和分带子午线长度是相等的,但是在投影到平面上之后,它们的长度明显不相等了(长度变长了),离开中央子午线越远,越不相等,即离开中央子午线越远,其变形越大。所以说,才要分带进行小范围投影,控制离开中央子午线处的变形。可见,高斯克吕格投影离开中央子午线的地方有变形。

注:
1.3°带分带和6°带分带也是国际上很多国家采用的分带方法。


注:
1.已知带号的话,可以算投影带的中央子午线的经度。
2.已知中央子午线经度的话,也可以算带号。


注:
1.投影的时候不是投影到分带子午线就停止了,而是再往外面扩展一点。
2.东带压西带15′,西带压东带30′。这样分带子午线附近的点就属于两个投影带了,在两个投影带里面就有个联系。


注:
1.横坐标y加上500公里,再冠以代号,也是国际上的做法,这完全是一种规定。实际上现在计算机时代,这个做法必要性也不是太大了,但是我们一般会沿用过去的习惯。
2.过去手工时代,抄写的时候,负号可能会忘记,或者一不小心抄错。


答:
1.地图投用就是建立椭球面和平面点的一一对应的函数关系。为何投影?因为椭球面大地坐标不能直接用来测图,我们平时用的地图是平面图,不是三维立体图,投影之后,在平面上的计算也会方便很多。
2.正形特性就是投影前后图形的角度保持不变,图形是相似的。
3.?


4.分带是为了控制投影的长度变形,假如不分带,则投影之后,离开中央子午线越远的地方,长度变形会很大。分带的方法有两种:6°带分带和3°带分带。
5.是高斯投影的一种改善,不要求中央子午线在投影前后长度保持不变,而要求中央子午线在投影后和投影前的长度比为0.9996,这样离开中央子午线两边的地方,投影变形会比高斯投影的投影变形小一些。

注:
1.第3条的柯西黎曼微分方程左边是椭球面到平面的微分关系式,右边是平面到椭球面的微分关系式。
2.要找的函数关系式是满足第3条(1)的微分方程的。或者说满足此偏微分方程的关系式就满足等角的特性。
3.偏微分方程就是根据图形在椭球面到平面投影前后的等角特性推出来的。

注:
1.正形特性+两个限制条件,可以推出偏微分方程的特解,从而得出椭球面到平面投影的函数关系式。
很多情况下,偏微分方程是不太好解的。

注:
1.实际上就是建立椭球面和平面上点的一一对应关系。
下面的任务是解偏微分方程:
如果一个方程很复杂,一般的话都会想办法按照级数展开,这个时候,函数会变成多项式。这个具有一般的解方程的参考意义。

注:
1.隐函数按照级数展开后,就相当于求多项式的待定系数就行了。
2.即便考虑投影重叠的话,经差也只在0~3.5°范围以内,3.5°化成弧度是:3.5/ρ=3.5/(180/pi)=0.061086524,很小。非常小的话,就可以把函数展开成经差L的幂级数,这是解决问题最关键的一步。
3.幂级数展开要看展开点在哪里,要在展开点处展开。
下面给出具体的函数展开过程:
在平面上任意取一个点P,展开点取教规所指的地方P0,这一点是中央子午线上的一个点:

【大地测量学基础】解放军信息工程大学丨含课件_哔哩哔哩_bilibili
下面对x,y的表达式进行泰勒级数展开。
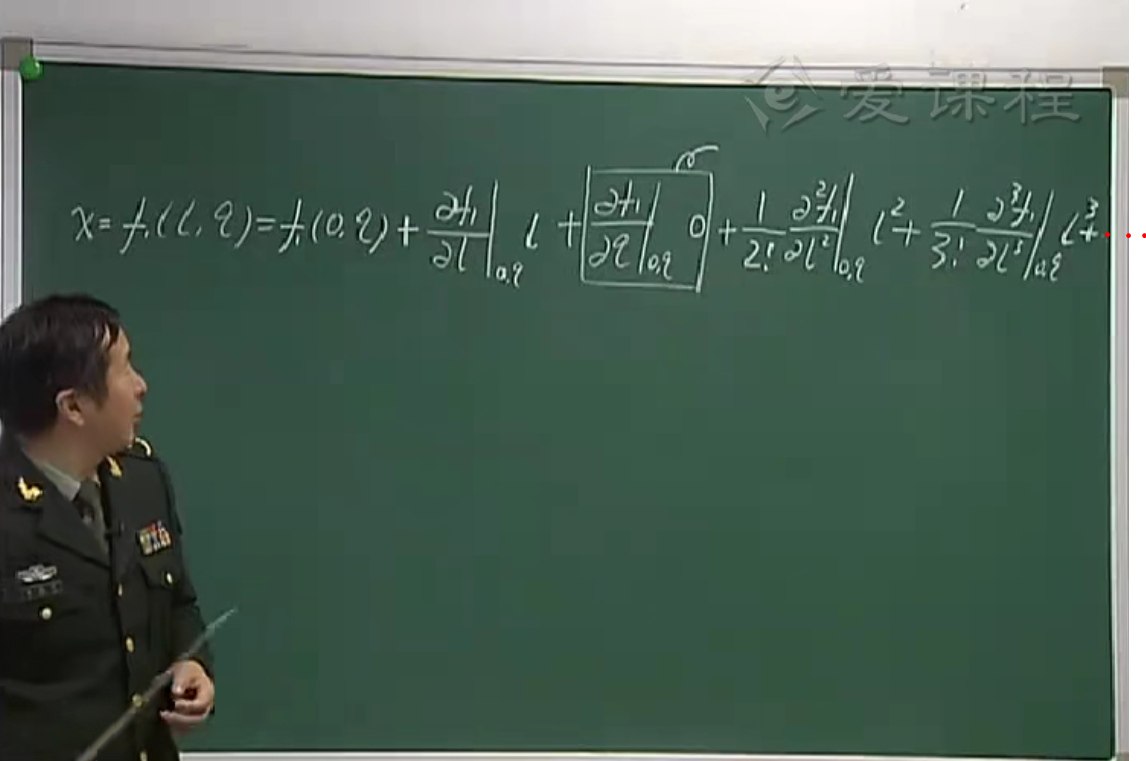
注:
1.在对x的表达式进行泰勒展开的时候,所有对q的偏导数项和混合偏导数项都是0,这是因为展开点处的纬差都是0。
2.所有的系数里面都不含经差l了,因为所有的系数带入是(0,q)。即:l=0常数带入,q=q带入.
3.在展开点处,纵坐标x=X.


注:
1.本来展开后各个偏导数的系数和混合偏导数系数中,是包含经差l的,但是系数中带入了l=0,所以也就不含l了。
2.m0是展开点处的纵坐标。n0是展开点处的横坐标。n0=0.
3.展开后各个多项式的系数mi,ni都是等量纬度q的函数了。
4.f1(0,q)是展开点(0,q)处的x值,f2(0,q)是展开点(0,q)处的y值。

注:
1.x、y本来是l、q的函数,现在展开成了l的幂级数的形式。

注:
1.利用高斯投影的2个附件条件解x,y泰勒级数展开式表达式中的待定系数。

在数学中,如果两个幂级数相等的话,那同次幂的系数应该相等的, 上面两个方程式可以得到两组方程:

注:
1.这两组方程是有规律的,很有意思,有递推特性,递推特性就是:假如n0知道,那么m1就知道,那么n2就会知道,那么m3就会知道,n4,m5,...就会知道。同样的,假如m0知道,那么n1,m2,n3,m4,n5,...就会知道。
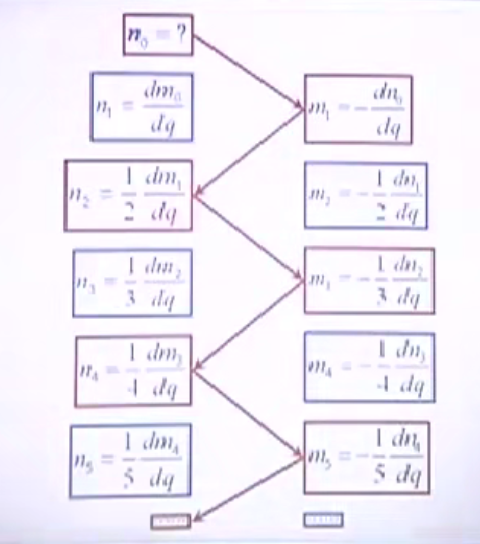


2.最后归结为n0,m0是什么?
3.要求出n0,m0,就要用到带2个附件条件的高斯投影,即用到高斯投影的2个附加条件。
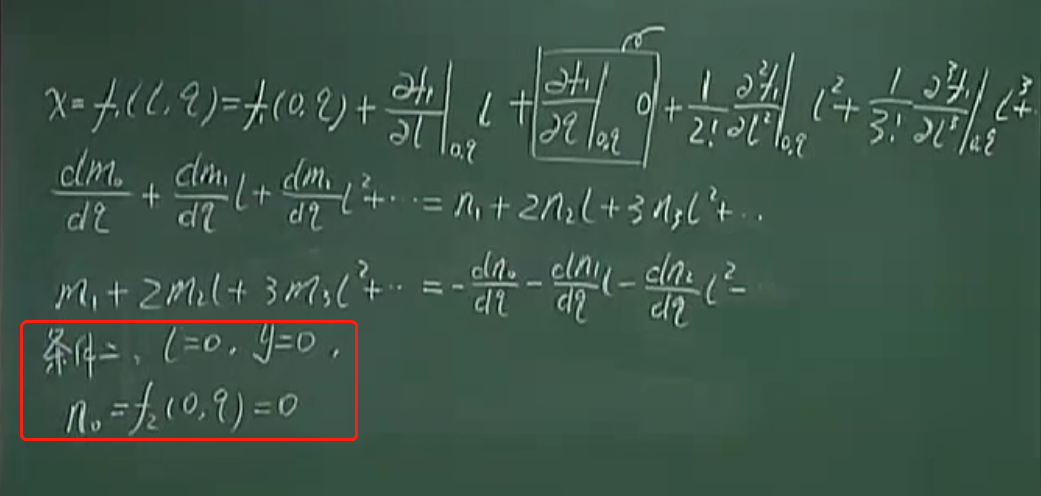
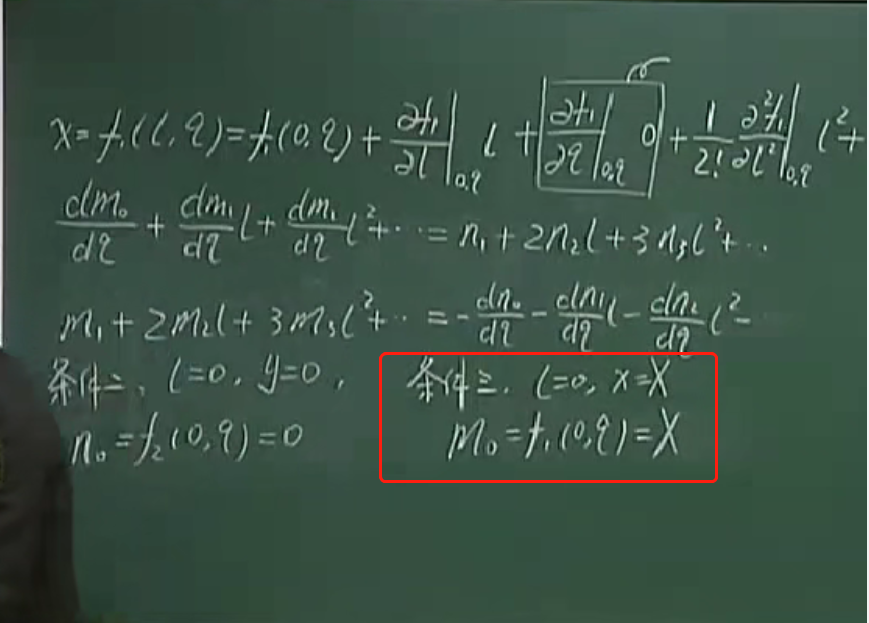
注:
1.经差l=0的时候(中央子午线上),x=X(投影前的子午线弧长)。
2.展开点处的x值就是m0.



注:
1.书上计算到经差l的5次幂。

注:
1.投影后的高斯平面坐标,跟什么量有关呢?答:

B,Δl:跟椭球面上的位置有关。
N(法线长):跟选择的椭球有关。
t:t=tanB,跟纬度有关
η:η=e2cosB,跟选择的椭球和纬度有关。e=sqrt(a2-b2)/a是第一偏心率。
2.展开到经差l的5次幂,精度能到分米级,还是有点低了(用于导航够了)。假如需要更高精度,就继续往高次幂写。
3.大地测量的精度要求是毫米级的,那就继续往下写,增加项数。

注:
1.这个是写到经差l的6次幂的形式,这个精度应该是到了毫米级了。

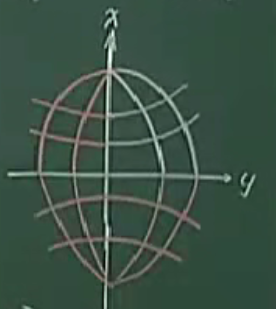
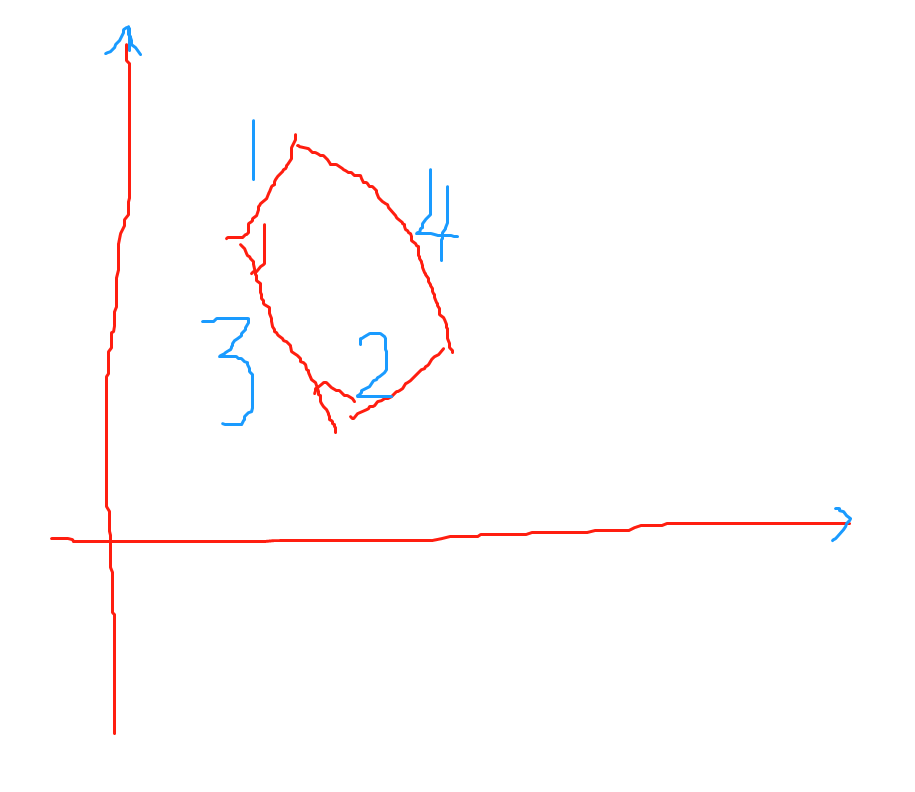
证明:如上图,1和2是平行圈弧素,3是大地线附近的子午线弧素,4是大地线弧素。


注:
1.X=?是子午线弧长公式(第五章学过)。计算的时候就以度为单位,量纲已经提前吸收到系数里面了。现在这个参数是克拉索夫斯基椭球子午线弧长公式,不是北京54参考椭球的子午线弧长公式,也不是CGCS2000椭球的子午线弧长公式。

高斯投影正算公式的结构:

x=X+...


下面求反算(高斯投影面的点对应到椭球面上的点)。
注:
1.6°带投影的高斯投影面上,y为300多公里,为何不大?假如按照有小重叠的6°带投影算的话,y值在椭球面上:
![]()
和地球半径比,它是个小量。因为上面的值除以地球半径的结果是:

从另一个角度看,q,l都是角度,6°带的投影,y值最大为3.5°,化成弧度就是:

2.展开的多项式里面,系数不含y了,只是x的函数。
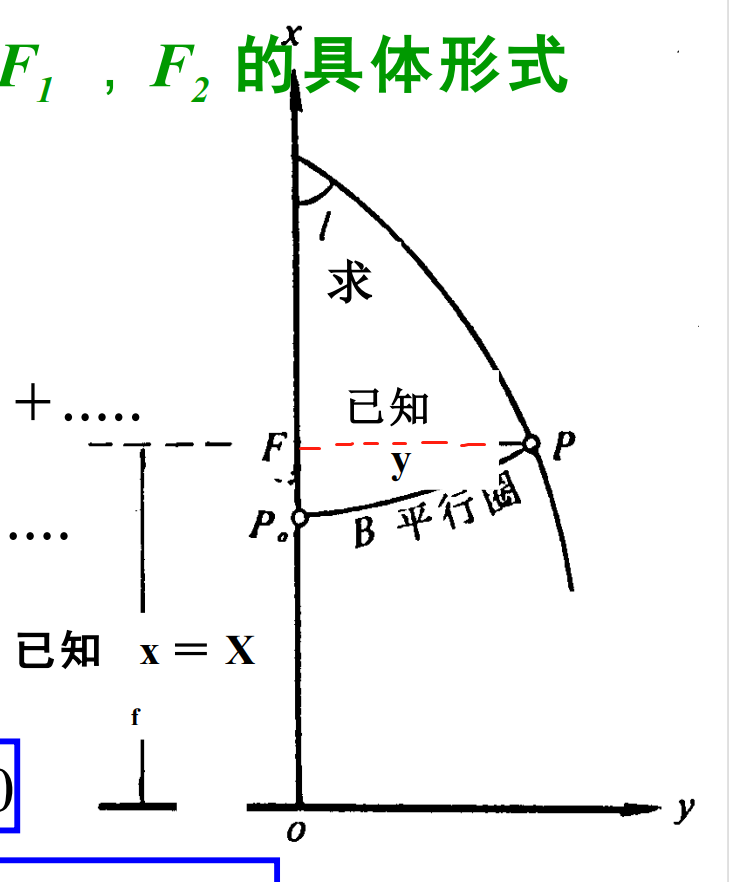
3.垂足点上的大地纬度,称为垂足纬度。Bf表示过这一点的垂足处的纬度值。下标是f的代表这一点的垂足处的量。如Xf表示垂足处的子午线弧长。在F点,x已知,投影前后,子午线弧长不发生改变,即它在椭球面上的子午线弧长已知,根据子午线弧长公式可以反算F点的纬度B。即Bf知道。那么等量纬度qf也就知道了。所以,只要带下标f的量都是已知的,

系数推导:
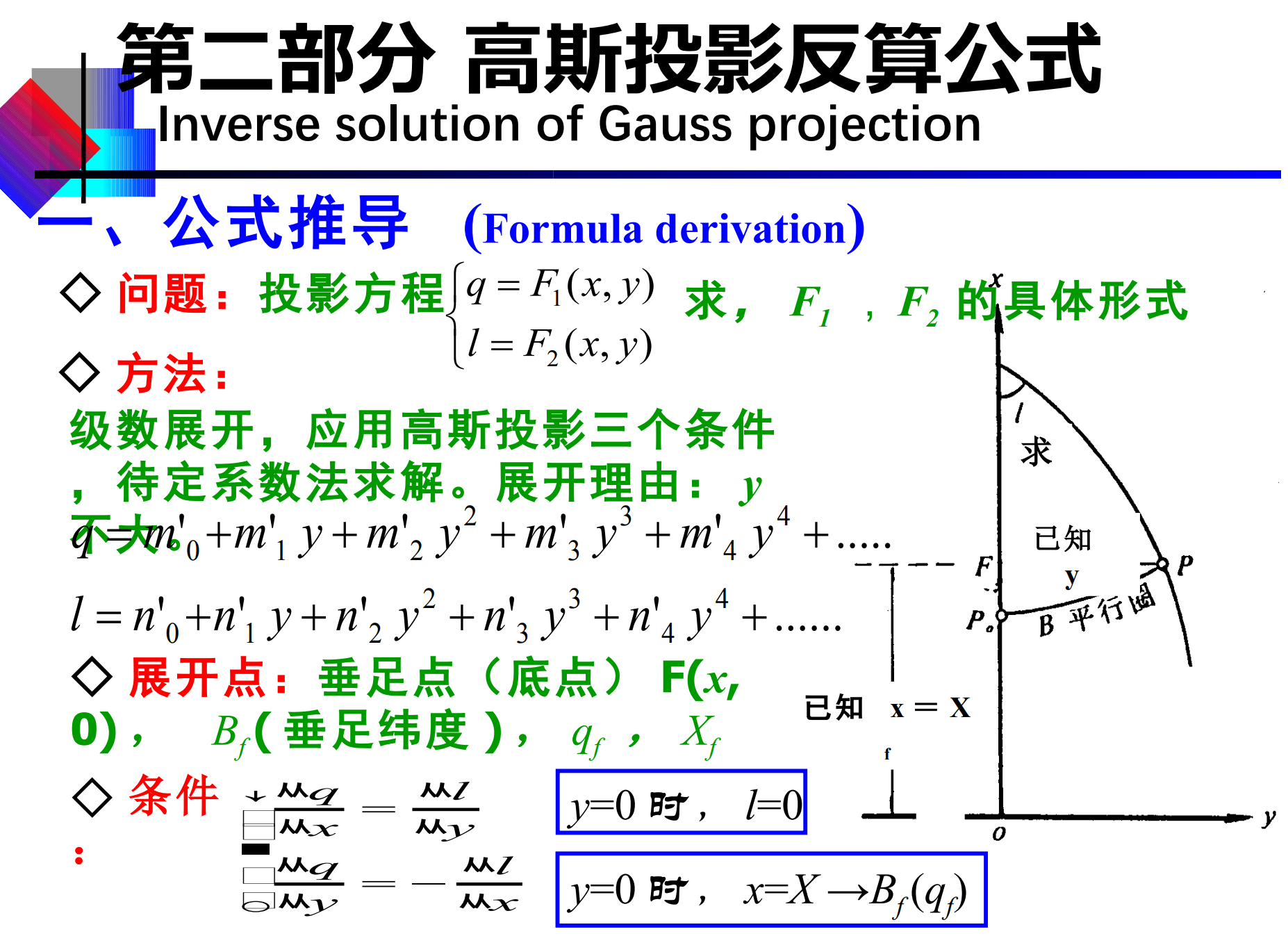

在高等数学中,幂级数相等意味着同次幂的系数相等,从而得到2组关系式(具有递推关系):

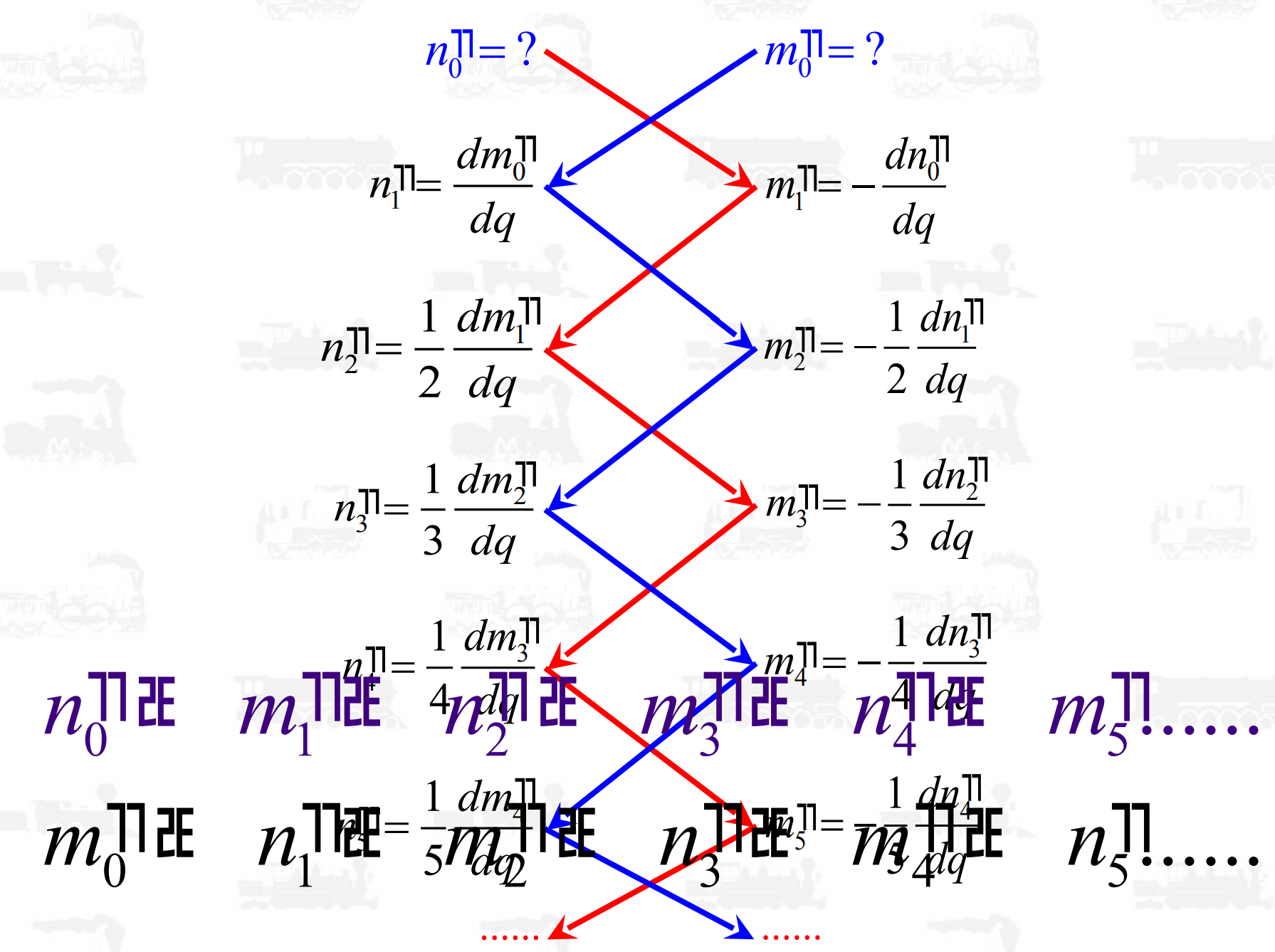
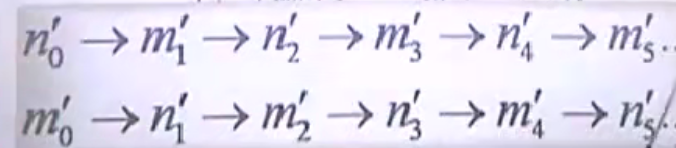
假如n0'和m0'知道,那其它的系数也就知道了。因为n0'=0,所以第一行的系数都等于0.
q=qf=m0'.所以:



注:
1.高斯投影反算是通过高斯平面上的一点坐标(x,y)对应到椭球面上的(L,B),y可以明显的在表达式中看见,那x跑哪里去了?所有下标带f的量都是通过x算出来的。x=X=椭球面上子午线弧长。
2.q化为B的时候,根据q和B的微分关系式,直接积分积不出来,所以把B=F(q)转换一下,按照泰勒级数在qf这一点展开。

下面给出以度为单位的高斯投影实用反算公式:


注:
1.已知X求B的时候,使用迭代的方法求取B值。红色横线上面的部分是克拉索夫斯基椭球子午线弧长对应纬度的关系式。
2.红色横线下面的部分是CGCS2000椭球的参数。高斯投影的反算到此结束。
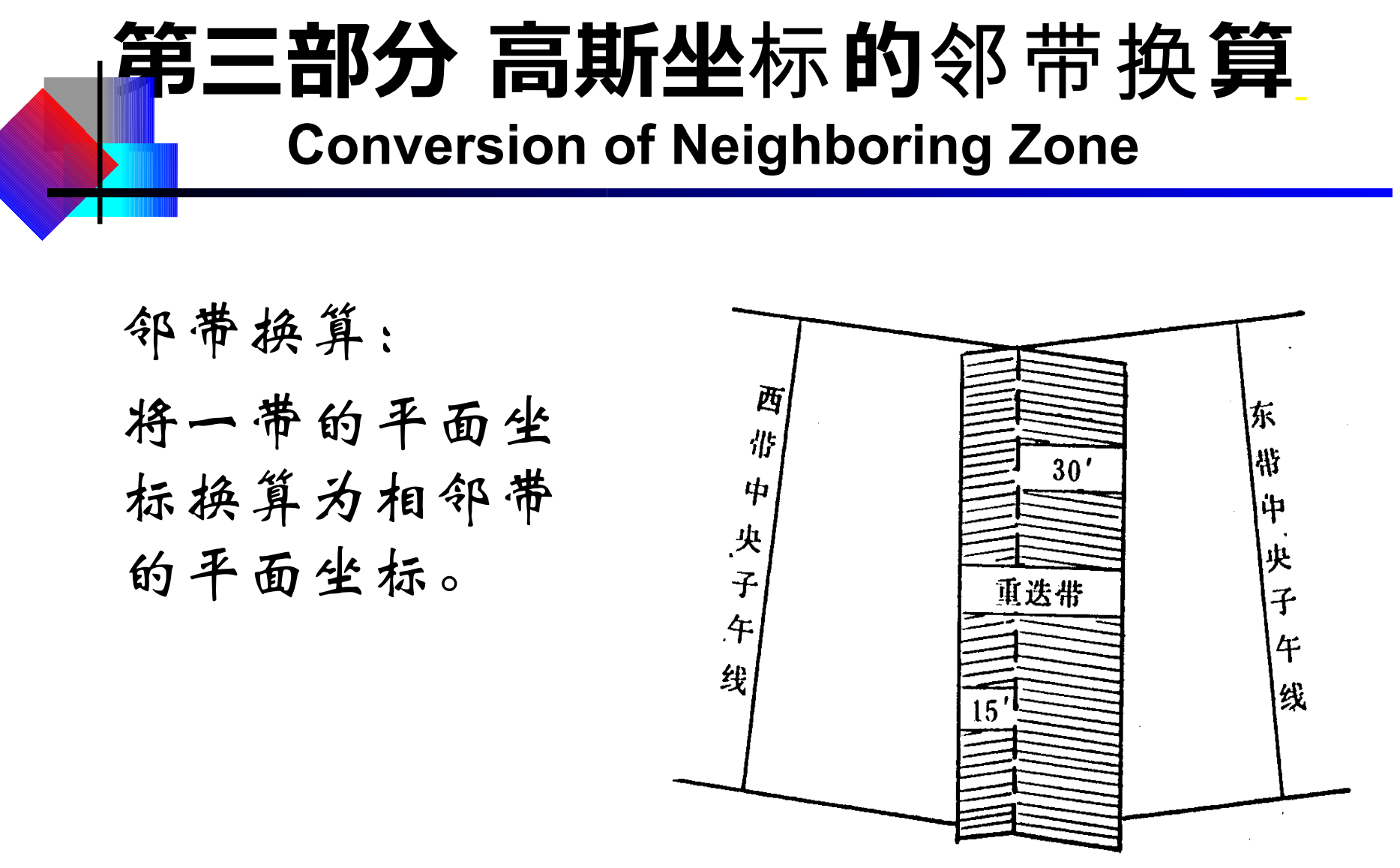
注:
1.高斯投影相邻两带之间没有任何的几何关系,没有图示的那样的几何关系,这只是一种示意图。

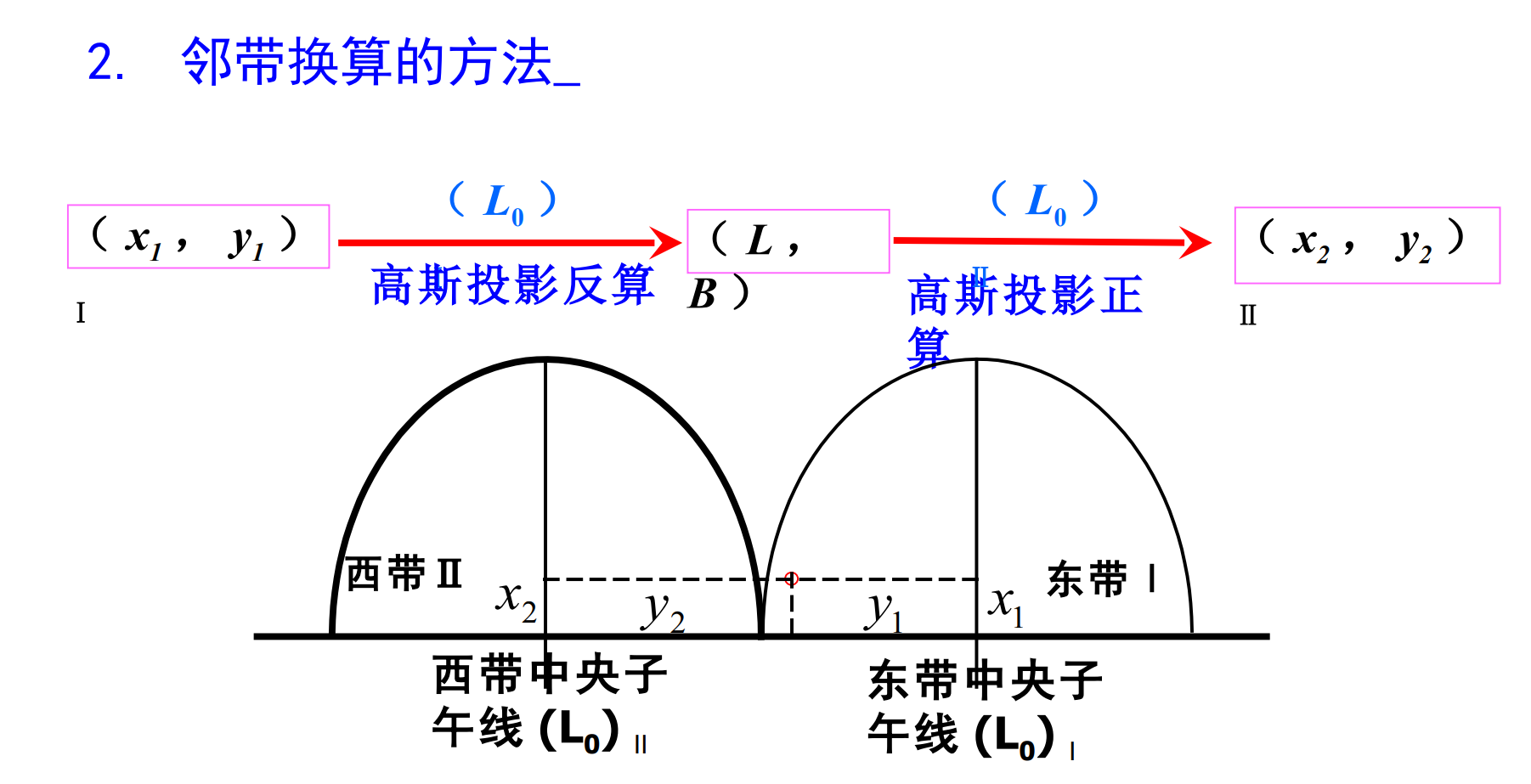

注:
1.两个带之间没有图示所示的几何关系,这只是一种示意图。
2.分带子午线1和2是同一个分带子午线。
3.高斯坐标反算B、L的时候要用到中央子午线经度,此时要选择东带的中央子午线经度,不要选成西带的中央子午线经度了。算出L、B之后,当进行高斯投影正算的时候,要用西带的中央子午线经度,不能用东带的中央子午线经度。假如用东带的中央子午线经度,又算回去了,算回到了(x1,y1).
4.高斯投影正反算公式的程序组合起来,就成了一个高斯投影邻带换算的程序了。
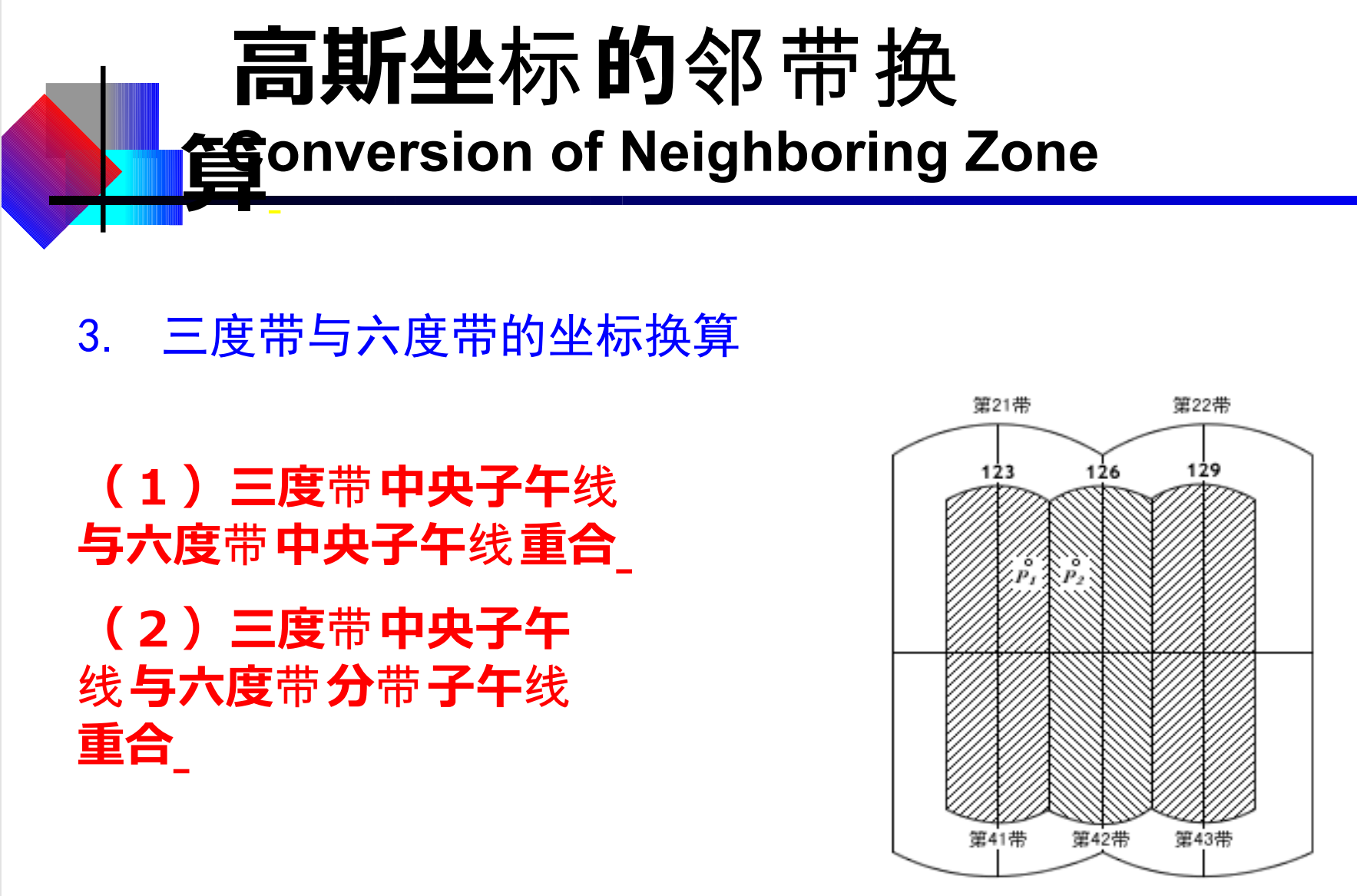
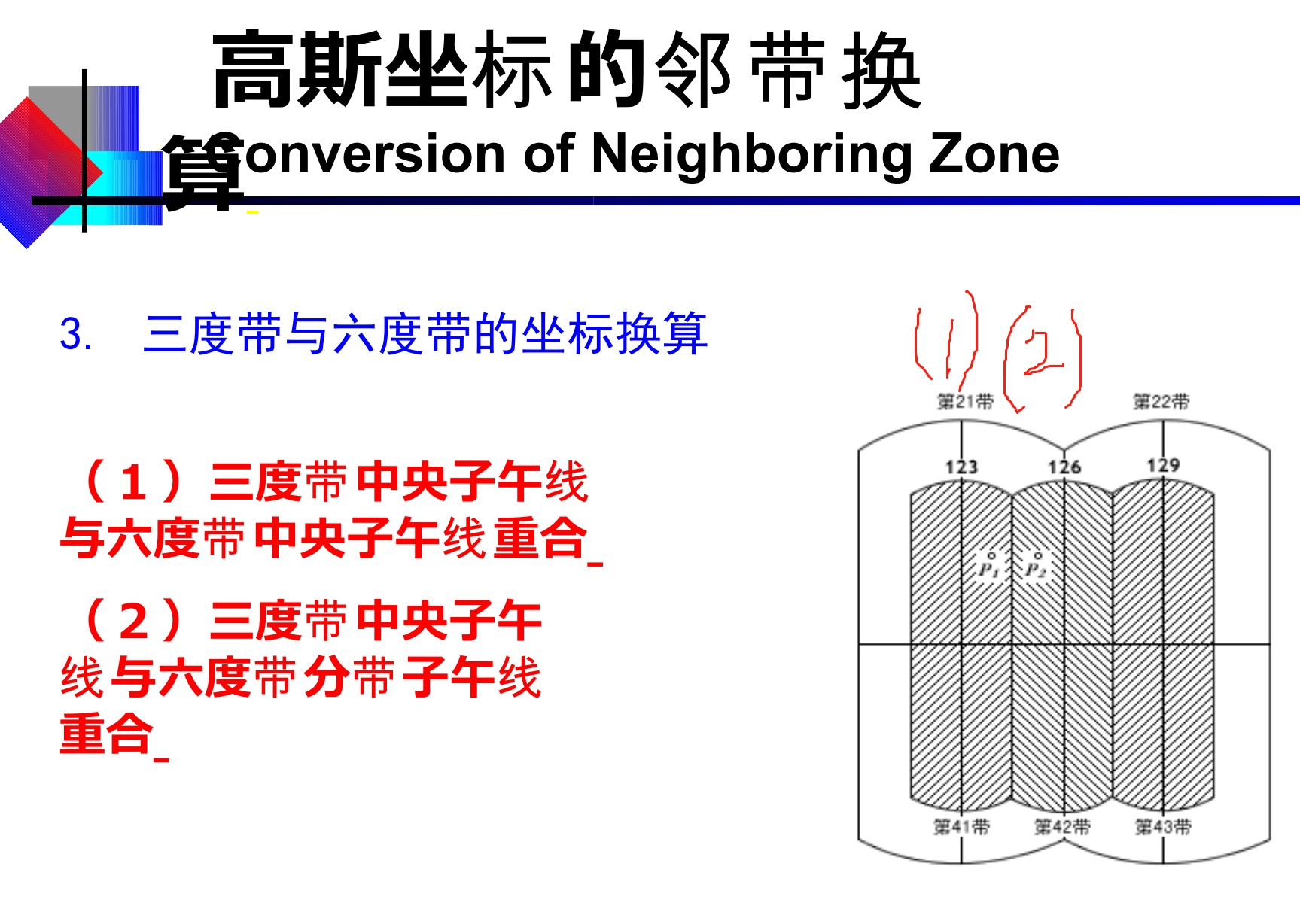
注:
1.6°带的第21带在我们国家范围内。
2.当中央子午线重合的时候,3°带的坐标和6°带的坐标不用换算。因为中央子午线一样的话,那投影后的高斯平面直角坐标系就是一样的。
3.3°带的中央子午线是6°带的分带子午线重合的时候,因为所使用的中央子午线不一样,必然导致高斯投影的坐标系纵轴不一样,所以要统一坐标系的话,坐标需要换算。方法仍然是先反算再正算。注意先反算后正算的时候选择的中央子午线经度是不一样的。

答:
1.高斯投影的3个条件:
a.正形(等角)投影(柯西黎曼微分方程);
b.中央子午线投影后仍然是直线(l=0,则y=0);
c.中央子午线投影后长度不变(l=0,则投影后纵坐标x=投影前子午线弧长X)。
2.垂足纬度是指投影后的高斯平面上,任意一点向坐标纵轴作垂线,垂足所在的位置的纬度就是垂足纬度。高斯投影正算公式的展开点在投影后的中央子午线纵轴上(1位置),高斯投影反算的展开点在垂足(纬度)处(2位置)。
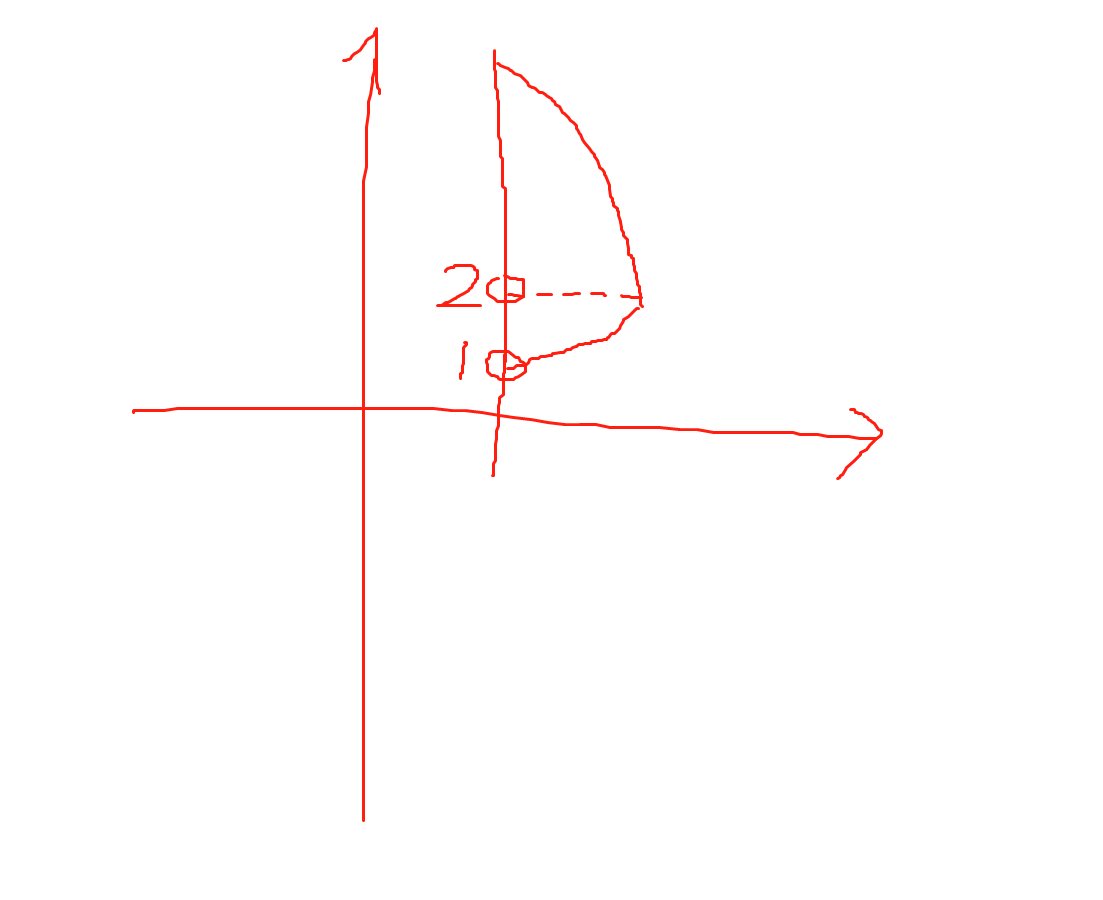
3.邻带换算是把跨越两个投影带的那些点的坐标换算到一个指定的投影带上。原理是先把(x,y)坐标利用高斯投影反算公式计算出这一点的在椭球面上的经纬度,然后再利用高斯投影正算计算出它在指定的投影带上的高斯平面直角坐标系中的坐标。注意计算的时候的中央子午线的选择不要选择错了,在进行高斯投影反算的时候,中央子午线选择的是(x,y)这一点所在带的中央子午线,不是要换算的那一个投影带的中央子午线。而在第2步高斯投影正算的时候,中央子午线经度选择的是要换算的那一个投影带的中央子午线经度。
3°带和6°带的换算:分为两种情况。情况1:3°带的中央子午线和6°带的中央子午线重合,此时不需要进行换算,因为虽然位于3°带和6°带里面,但是投影后的高斯平面直角坐标系是一样的,坐标纵轴和坐标横轴都完全一样,既然使用的坐标系一样,那同一个位置的坐标投影后当然也会一样。情况2:3°带的中央子午线是6°带的分带子午线,此时就需要把(x,y)这一点先利用高斯投影反算算出它在椭球面上大地坐标(即大地经纬度),然后再利用高斯投影正算计算它在新的投影带里面的高斯坐标。在进行高斯投影正反算的时候,同样需要注意中央子午线的选择不要选择错了。
假如有时间的话,就看:【大地测量学基础】解放军信息工程大学丨含课件_哔哩哔哩_bilibili
以上是椭球面到高斯投影面上一个点的投影,下面还需要讨论椭球面到高斯投影面的一个图形的投影。


注:
1.之前已经把地面上的控制网归算到了椭球面上,现在要把椭球面上的控制网元素归算到高斯投影面上。
2.S12是椭球面上的大地线,投影到平面上去之后是D12右边的虚线(椭球面上大地线进行高斯投影后的线是凹向中央子午线的曲线)。需要把它转换成直线表示的距离D12.
3.大地方位角A12,需要换算成高斯投影面上的坐标方位角T12.




