42行代码完成深入虎穴
题目:
著名的王牌间谍 007 需要执行一次任务,获取敌方的机密情报。已知情报藏在一个地下迷宫里,迷宫只有一个入口,里面有很多条通路,每条路通向一扇门。每一扇门背后或者是一个房间,或者又有很多条路,同样是每条路通向一扇门…… 他的手里有一张表格,是其他间谍帮他收集到的情报,他们记下了每扇门的编号,以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。
内线告诉他,情报就藏在迷宫的最深处。但是这个迷宫太大了,他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。
输入格式:
输入首先在一行中给出正整数 N(<10的五次方),是门的数量。最后 N 行,第 i 行(1≤i≤N)按以下格式描述编号为 i 的那扇门背后能通向的门:5),是门的数量。最后 N 行,第 i 行(1≤i≤N)按以下格式描述编号为 i 的那扇门背后能通向的门:
K D[1] D[2] ... D[K]
其中 K 是通道的数量,其后是每扇门的编号。
输出格式:
在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。
输入样例:
13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0
输出样例:
12
分析:
这道题目本身的理解并不难,只需要找到合适的数据存储方式构建树,再利用BFS遍历找到最后一层的数据即可。
但如何能找到合适的数据存储方式呢?(难点)
针对这道题目,二维数组显然是最简单最直观的解决方法。但由于题目的数据量较大,不能够用常规的静态二维数组完成(会导致超时等问题)。
这里动态的二维数组,在一维数组(存放节点编号)的基础上再接上一个一维数组存放该节点的子节点信息。
这里使用vector建立动态二维数组。
如图:(输入样例)
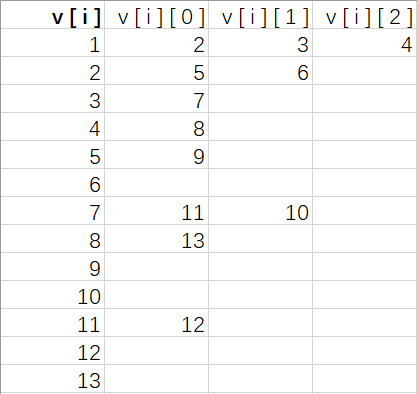
思路都写在代码的注释里了~
代码:
1 #include<iostream> 2 #include<queue> 3 #include<vector> 4 #include<cstring> 5 using namespace std; 6 7 const int maxn = 100009; 8 queue <int> qu; 9 vector <int> v[maxn]; 10 int check[maxn]; 11 12 int main() 13 { 14 int i, n, child, num_child, root=-1; 15 memset(check, 0, sizeof(check));//memset函数,将数组元素初始化为0 16 cin>>n;//输入节点个数 17 for(i=1; i<=n; i++){ 18 cin>>num_child;//输入孩子个数 19 while(num_child-- != 0){ 20 cin>>child;//输入孩子 21 check[child]++; 22 v[i].push_back(child);//将孩子存入vector v中;动态二维数组 23 } 24 } 25 26 for(i=1; i<=n; i++){ 27 if(check[i] == 0){ 28 root = i; 29 break; 30 } 31 } 32 qu.push(root);//根节点入队 33 while(qu.size() != 0){ 34 root = qu.front();//定位到当前队头元素x 35 qu.pop();//队头元素x出队 36 for(i=0; i<v[root].size(); i++){ 37 qu.push(v[root][i]);//x的子节点入队 38 } 39 } 40 cout<<root; 41 return 0; 42 }
总结:
树是一种在实际运用中具有局限性的数据结构,往往只有在确定题目所求、输入格式之后才能敲定应该利用那种存储方式来存储数据,进而利用数据来构建树。
因此在利用树解决问题的过程中,难点往往在构建树,当一棵健康的树建立好之后,后面的问题也就可以迎刃而解了。
磨刀不误砍柴工。
分析过程比直接上手操作效率来得更高。





