kuangbin 专题一：G题，POJ3087：Shuffle'm Up

POJ3087：Shuffle'm Up

kuangbin  专题一：G题

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 12455		Accepted: 5780

Description

A common pastime for poker players at a poker table is to shuffle stacks of chips. Shuffling chips is performed by starting with two stacks of poker chips, S₁ and S₂, each stack containing C chips. Each stack may contain chips of several different colors.

The actual shuffle operation is performed by interleaving a chip from S₁ with a chip from S₂ as shown below for C = 5:

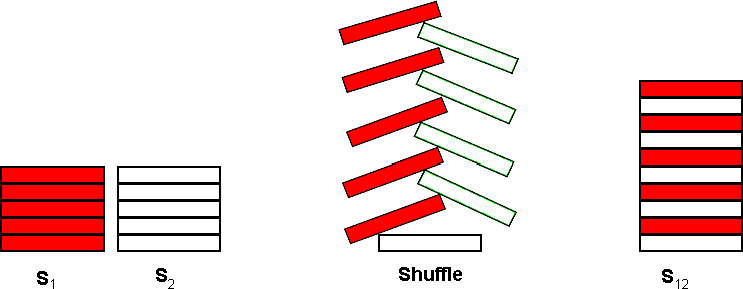
The single resultant stack, S₁₂, contains 2 * C chips. The bottommost chip of S₁₂ is the bottommost chip from S₂. On top of that chip, is the bottommost chip from S₁. The interleaving process continues taking the 2^nd chip from the bottom of S₂ and placing that on S₁₂, followed by the 2^nd chip from the bottom of S₁ and so on until the topmost chip from S₁ is placed on top of S₁₂.

After the shuffle operation, S₁₂ is split into 2 new stacks by taking the bottommost C chips from S₁₂ to form a new S₁ and the topmost C chips from S₁₂ to form a new S₂. The shuffle operation may then be repeated to form a new S₁₂.

For this problem, you will write a program to determine if a particular resultant stack S₁₂ can be formed by shuffling two stacks some number of times.

Input

The first line of input contains a single integer N, (1 ≤ N ≤ 1000) which is the number of datasets that follow.

Each dataset consists of four lines of input. The first line of a dataset specifies an integer C, (1 ≤ C ≤ 100) which is the number of chips in each initial stack (S₁ and S₂). The second line of each dataset specifies the colors of each of the C chips in stack S₁, starting with the bottommost chip. The third line of each dataset specifies the colors of each of the C chips in stack S₂ starting with the bottommost chip. Colors are expressed as a single uppercase letter (A through H). There are no blanks or separators between the chip colors. The fourth line of each dataset contains 2 * C uppercase letters (A through H), representing the colors of the desired result of the shuffling of S₁ and S₂ zero or more times. The bottommost chip’s color is specified first.

Output

Output for each dataset consists of a single line that displays the dataset number (1 though N), a space, and an integer value which is the minimum number of shuffle operations required to get the desired resultant stack. If the desired result can not be reached using the input for the dataset, display the value negative 1 (−1) for the number of shuffle operations.

Sample Input

2
4
AHAH
HAHA
HHAAAAHH
3
CDE
CDE
EEDDCC

Sample Output

1 2
2 -1
题意：n组数据 两堆 扑克 长度都为C 给出两堆扑克按一定操作后的 目标扑克堆（两堆扑克的综合）
　　　从下向上 按照一张 2堆扑克 一张 1堆扑克  顺堆放 。 计算得到目标 扑克需要多少次操作 
　　　如果不能得到目标扑克堆 操作数为 -1 
思路： 由题意 模拟对扑克的操作 ， 最重要的是想到 扑克操作的终止条件 ， 
　　　终止条件： 如果对扑克的操作 出现循环 且没有得到目标堆 说明不可能得到  目标扑克堆 操作数为 -1 
AC代码 ：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std ; 

#define maxn 150 
char str_1[maxn] ; 
char str_2[maxn] ; 
char st[maxn * 2] ; // 正在模拟的扑克堆 
char result[maxn * 2] ; // 目标扑克堆 
char Ends[maxn*2] ; // 终止条件 

int main(){
    int n ; 
    scanf("%d" , &n) ; 
    int Case = 0 ; 
    while(n--){
        int c ; 
        scanf("%d" , &c) ; 
        scanf("%s %s %s" , str_1 , str_2 , result ) ; 
        strcpy(st , str_1) ; 
        strcat(st , str_2) ; 
        strcpy(Ends , st) ; 
        
        int times = 0 ; 
        for(times = 0 ; strcmp(result , st ) !=0 ; times++){
            // 模拟操作  
            for(int i=0 ; i < c ; i++){
                str_1[i] = st[i] ; 
            }
            for(int i=0 ; i<c ; i++){
                str_2[i] = st[i+c] ; 
            }
            for(int i=0 ; i<c ; i++){
                st[2*i] = str_2[i] ; 
                st[2*i+1] = str_1[i] ; 
            }
            // 出现循环 且没有得到目标堆 
            if(strcmp(Ends , st) == 0 ){
                 
                times = -1 ; 
                break ; 
            }
            
        }
        printf("%d %d\n" , ++Case , times) ; 
    }
    return 0; 
}