2017年ACM第八届山东省赛I题： Parity check（判断 第n项斐波那契数列奇偶性）

I: Parity check

题目描述

Fascinated with the computer games, Gabriel even forgets to study. Now she needs to finish her homework, and there is an easy problem:

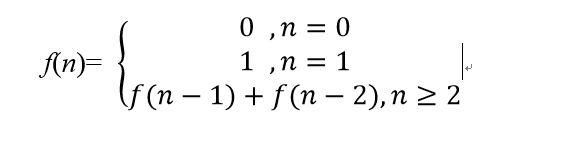
She is required to calculate f(n) mod 2 for each given n. Can you help her?

输入

Multiple test cases. Each test case is an integer n(0≤n≤10¹⁰⁰⁰) in a single line.

输出

For each test case, output the answer of f(n)mod2.

样例输入

2

样例输出

1
题意：第一眼看过去以为是  斐波那契数列（矩阵快速幂），仔细一看才知道是 斐波那契数列求奇偶（mod%2）
思路：打表 斐波那契数列 前几项：
　前 22 项
0：0
1：1
2：1
3：2
4：3
5：5
6：8
7：13
8：21
9：34
10：55
11：89
12：144
13：233
14：377
15：610
16：987
17：1597
18：2584
19：4181
20：6765
21：10946
编号为 n 的 斐波那契数列 只要 n%3==0 fac（n）%3 == 0 
否则 fac（n） %3 == 1 ； 

然后就是 数字 n 比较长 需要 字符串输入 然后 char 转 int 同时 对 3 取模

#include <cstdio>
#include <cstring>
int main(){
    int n ; 
    char str[2000] ; 
    while(~scanf(" %s" , str)){
        int len = strlen(str) ; 
        int sum =0;
        for(int i=0 ; i<len ; i++){
            sum = (sum*10 + str[i]-'0') % 3 ; 
        }
        if(sum %3==0){
            printf("0\n") ; 
        }else printf("1\n") ; 
    } 
    return 0 ; 
}

 或者 （n 能被三整除 则 n 的各个数字和相加也能被三整除）

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
char str[1005];
int main()
{
    int n, i, j, k, sum;
    while (scanf("%s", str) != EOF)
    {
        sum = 0;
        for (int i = 0;str[i] != '\0';i++)
            sum += (str[i] - '0');
        if (sum % 3 == 0) printf("0\n");
        else printf("1\n");
    }
    return 0;
}