Faiss流程与原理分析

 1、Faiss简介

　　Faiss是Facebook AI团队开源的针对聚类和相似性搜索库，为稠密向量提供高效相似度搜索和聚类，支持十亿级别向量的搜索，是目前最为成熟的近似近邻搜索库。它包含多种搜索任意大小向量集（备注：向量集大小由RAM内存决定）的算法，以及用于算法评估和参数调整的支持代码。Faiss用C++编写，并提供与Numpy完美衔接的Python接口。除此以外，对一些核心算法提供了GPU实现。相关介绍参考《Faiss：Facebook 开源的相似性搜索类库》

 2、Faiss安装

　　参考《faiss_note/1.Install faiss安装.ipynb》，此文是对英文版本的翻译，便于查看。

      基于本机环境，采用了anaconda进行安装，这也是faiss推荐的方式，facebook研发团队也会及时推出faiss的新版本conda安装包，在conda安装时会自行安装所需的libgcc, mkl, numpy模块。

      针对mac os系统，可以先安装Homebrew（mac下的缺失包管理，比较方便使用）。

　　安装anaconda的命令如下所示：

#安装anaconda包
brew cask install anaconda
#conda加入环境变量
export PATH=/usr/local/anaconda3/bin:"$PATH"
#更新conda
conda update conda
#先安装mkl
conda install mkl
#安装faiss-cpu
conda install faiss-cpu -c pytorch
#测试安装是否成功
python -c "import faiss”

　　备注：mkl全称Intel Math Kernel Library，提供经过高度优化和大量线程化处理的数学例程，面向性能要求极高的科学、工程及金融等领域的应用。MKL是一款商用函数库（考虑版权问题，后续可以替换为OpenBLAS），在Intel CPU上，MKL的性能要远高于Eigen, OpenBLAS和其性能差距不是太大，但OpenBLAS提供的函数相对较少，另外OpenBLAS的编译依赖系统环境。

 3、Faiss原理及示例分析

  3.1 Faiss核心算法实现

　　Faiss对一些基础的算法提供了非常高效的失效

• 聚类Faiss提供了一个高效的k-means实现
• PCA降维算法
• PQ(ProductQuantizer)编码/解码

  3.2 Faiss功能流程说明

       通过Faiss文档介绍可以了解faiss的主要功能就是相似度搜索。如下图所示，以图片搜索为例，所谓相似度搜索，便是在给定的一堆图片中，寻找出我指定的目标最像的K张图片，也简称为KNN（K近邻）问题。

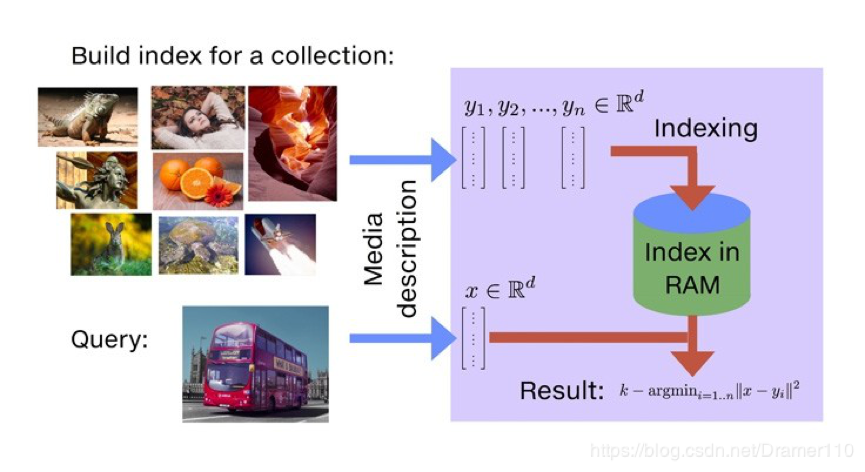
　　为了解决KNN问题，在工程上需要实现对已有图库的存储，当用户指定检索图片后，需要知道如何从存储的图片库中找到最相似的K张图片。基于此，我们推测Faiss在应用场景中具备添加功能和搜索功能，有了添加相应的修改和删除功能也会接踵而来，从上述分析看，Faiss本质上是一个向量（矢量）数据库。

      对于数据库来说，时空优化是两个永恒的主题，即在存储上如何以更少的空间来存储更多的信息，在搜索上如何以更快的速度来搜索出更准确的信息。如何减少搜索所需的时间？在数据库中很最常见的操作便是加各种索引，把各种加速搜索算法的功能或空间换时间的策略都封装成各种各样的索引，以满足各种不同的引用场景。

 3.3 组件分析

      Faiss中最常用的是索引Index，而后是PCA降维、PQ乘积量化，这里针对Index和PQ进行说明，PCA降维从流程上都可以理解。

  3.3.1索引Index

      Faiss中有两个基础索引类Index、IndexBinary，下面我们先从类图进行分析。

　　下面给出Index和IndexBinary的类图如下所示：

　　Faiss提供了针对不同场景下应用对Index的封装类，这里我们针对Index基类进行说明。

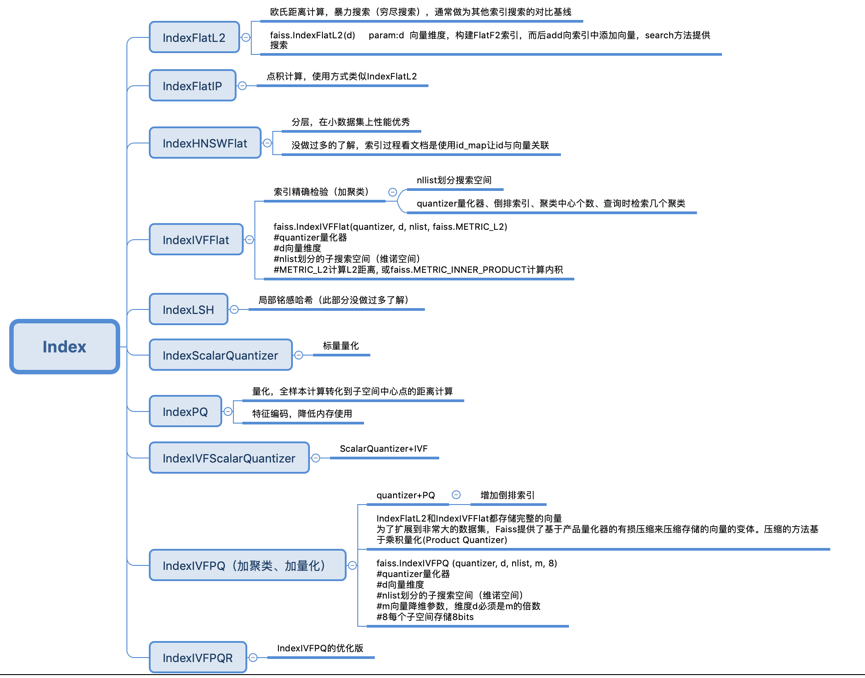
　　基础索引的说明参考：Faiss indexes涉及方法解释、参数说明以及推荐试用的工厂方法创建时的标识等。

      索引的创建提供了工厂方法，可以通过字符串灵活的创建不同的索引。

index = faiss.index_factory(d,"PCA32,IVF100,PQ8 ")

　　该字符串的含义为：使用PCA算法将向量降维到32维, 划分成100个nprobe (搜索空间), 通过PQ算法将每个向量压缩成8bit。

　　其他的字符串可以参考上文给出的Faiss indexes链接中给出的标识。

 3.3.1.1索引说明

　　此部分对索引id进行说明，此部分的理解是基于PQ量化及Faiss创建不同的索引时选择的量化器而来，可能会稍有偏差，不影响对Faiss的使用操作。

      默认情况，Faiss会为每个输入的向量记录一个次序id，也可以为向量指定任意我们需要的id。部分索引类（IndexIVFFlat/IndexPQ/IndexIVFPQ等）有add_with_ids方法，可以为每个向量对应一个64-bit的id，搜索的时候返回此id。此段中说明的id从我的角度理解就是索引。（备注：id是long型数据，所有的索引id类型在Index基类中已经定义，参考类图中标注，typedef long idx_t;    ///< all indices are this type）

      示例：

import numpy as np
import faiss                   # make faiss available

# 构造数据
import time
d = 64                           # dimension
nb = 1000000                      # database size
nq = 1000000                       # nb of queries
np.random.seed(1234)             # make reproducible
xb = np.random.random((nb, d)).astype('float32')
xb[:, 0] += np.arange(nb) / 1000.
xq = np.random.random((nq, d)).astype('float32')
xq[:, 0] += np.arange(nq) / 1000.

# 为向量集构建IndexFlatL2索引，它是最简单的索引类型，只执行强力L2距离搜索
index = faiss.IndexFlatL2(d)   # build the index
# #此处索引是按照默认方式，即faiss给的次序id为主
# #可以添加我们需要的索引方式，因IndexFlatL2不支持add_with_ids方法，需要借助IndexIDMap进行映射，代码如下
# ids = np.arange(100000, 200000)  #id设定为6位数整数，默认id从0开始，这里我们将其设置从100000开始
# index2 = faiss.IndexIDMap(index)
# index2.add_with_ids(xb, ids)
#
# print(index2.is_trained)
# # index.add(xb)                  # add vectors to the index
# print(index2.ntotal)
# k = 4   # we want to see 4 nearest neighbors
# D, I = index2.search(xb[:5], k) # sanity check
# print(I)     # 向量索引位置
# print(D)     # 相似度矩阵

print(index.is_trained)
index.add(xb)                  # add vectors to the index
print(index.ntotal)
k = 4   # we want to see 4 nearest neighbors
# D, I = index.search(xb[:5], k) # sanity check
# # print(xb[:5])
# print(I)     # 向量索引位置
# print(D)     # 相似度矩阵

D, I = index.search(xq, 10)     # actual search
# xq is the query data
# k is the num of neigbors you want to search
# D is the distance matrix between xq and k neigbors
# I is the index matrix of k neigbors
print(I[:5])                   # neighbors of the 5 first queries
print(I[-5:]) # neighbors of the 5 last queries

#从index中恢复数据，indexFlatL2索引就是将向量进行排序
# print(xb[381])
# print(index.reconstruct(381))

 3.3.1.2索引选择

      此部分没做实践验证，对Faiss给的部分说明进行翻译过来作为后续我们使用的一个参考。

      如果关心返回精度，可以使用IndexFlatL2，该索引能确保返回精确结果。一般将其作为baseline与其他索引方式对比，以便在精度和时间开销之间做权衡。不支持add_with_ids，如果需要，可以用“IDMap”给予任意定义id。

      如果关注内存开销，可以使用“..., Flat“的索引，"..."是聚类操作，聚类之后将每个向量映射到相应的bucket。该索引类型并不会保存压缩之后的数据，而是保存原始数据，所以内存开销与原始数据一致。通过nprobe参数控制速度/精度。

      对内存开销比较关心的话，可以在聚类的基础上使用PQ成绩量化进行处理。

  3.3.1.3检索数据恢复

      Faiss检索返回的是数据的索引及数据的计算距离，在检索获得的索引后需要根据索引将原始数据取出。

      Faiss提供了两种方式，一种是一条一条的进行恢复，一种是批量恢复。

　　给定id，可以使用reconstruct进行单条取出数据；可以使用reconstruct_n方法从index中回批量复出原始向量（备注：该方法从给的示例看是恢复连续的数据（0，10），如果索引是离散的话恢复数据暂时还没做实践）。

　　上述方法支持IndexFlat, IndexIVFFlat (需要与make_direct_map结合), IndexIVFPQ(需要与make_direct_map结合)等几类索引类型。

  3.3.2PCA降维

      具体的算法流程没有进行深入的了解，可以参考看：《PCA 降维算法详解 以及代码示例》，待后续算法学习中在进行深入了解。

      基于3.2节中对Faiss流程的说明，简要说下对Faiss中PCA的理解。

      PCA通过数据压缩减少内存或者硬盘的使用以及数据降维加快机器学习的速度。从数据存储的角度，图片处理中通过PCA可以将图片从高维空间（p维）转换到低维空间（q维, 其中p > q ），其具体操作便是是将高维空间中的图片向量（n*p）乘以一个转换矩阵（p*q），得到一个低维空间中的向量（n*q）。

　　为了使得在整个降维的过程中信息丢失最少，我们需要对待转换图片进行分析计算得到相应的转换矩阵（p*q）。也就是说这个降维中乘以的转换矩阵是与待转换图片息息相关的。回到我们的Faiss中来，假设我期望使用PCA预处理来减少Index中的存储空间，那在整个处理流程中，除了输入搜索图库外，我必须多输入一个转换矩阵，但是这个转换矩阵是与图库息息相关的，是可以由图库数据计算出来的。如果把这个转换矩阵看成一个参数的话，我们可以发现，在Faiss的一些预处理中，我们会引入一些参数，这些参数又无法一开始由人工来指定，只能通过喂样本来训练出来，所以Index中需要有这样的一个train() 函数来为这种参数的训练提供输入训练样本的接口。

  3.3.3Product quantization(乘积量化PQ)

      Faiss中使用的乘积量化是Faiss的作者在2011年发表的论文，参考：《Product Quantization for Nearest Neighbor Search》

      PQ算法可以理解为首先把原始的向量空间分解为m个低维向量空间的笛卡尔积，并对分解得到的低维向量空间分别做量化。即是把原始D维向量（比如D=128）分成m组（比如m=4），每组就是D∗=D/m维的子向量（比如D∗=D/m=128/4=32），各自用kmeans算法学习到一个码本，然后这些码本的笛卡尔积就是原始D维向量对应的码本。用qj表示第j组子向量，用Cj表示其对应学习到的码本，那么原始D维向量对应的码本就是C=C1×C2×…×Cm。用k∗表示子向量的聚类中心点数或者说码本大小，那么原始D维向量对应的聚类中心点数或者说码本大小就是k=(k∗)m。

      示例参考《实例理解product quantization算法》。