树状数组

树状数组

基本用途：维护序列的前缀和。

对于给定的序列a，我们建立一个数组c，其中从c[x]保存序列a的区间[x-lowbit(x)+1,x]中所有数的和。

数组c可以看作一个如下图所示的树形结构：

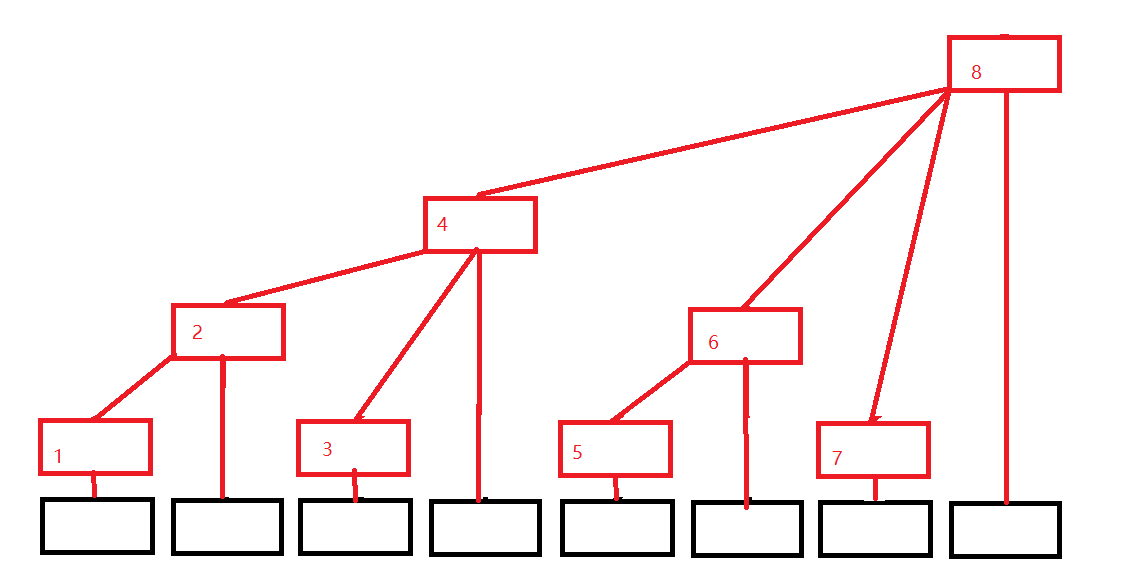
图中最下边一行是n个节点，代表数值a[1~n]。该结构满足以下性质：

• 每个内部节点c[x]保存以它为根的子树中所有叶节点的和；
• 每个内部节点c[x]的子节点个数=lowbit(x)的位数；
• 除树根外，每个内部节点c[x]的父节点是c[x+lowbit(x)]；
• 树的深度为O(logn)。

1.单点修改，区间查询

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[155000],c[155000];
int lowbit(int x){
	return x&-x;
}
void add(int x,int key){
	while(x<=n){
		c[x]+=key;
		x+=lowbit(x);
	}
}
int getsum(int x){
	int res=0;
	while(x){
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		add(i,a[i]);
	}
	scanf("%d",&m);
    string str;
	int x,y;
	for(int i=1;i<=m;i++){
		cin>>str>>x>>y;
		if(str[0]=='S'){
			printf("%d\n",getsum(y)-getsum(x-1));
		}
		else{
			add(x,y);
		}
	}
	return 0;
} 

2.区间修改，单点查询

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[155000],c[155000];
int lowbit(int x){
	return x&-x;
}
void add(int x,int key){
	while(x<=n){
		c[x]+=key;
		x+=lowbit(x);
	}
}
int getsum(int x){
	int res=0;
	while(x){
		res+=c[x];
		x-=lowbit(x);
	}
	return res;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		add(i,a[i]-a[i-1]);
	}
	scanf("%d",&m);
    string str;
	int x,y,z;
	for(int i=1;i<=m;i++){
		cin>>str;
		if(str[0]=='Q'){
		    cin>>x;
			printf("%d\n",getsum(x));
		}
		else{
			cin>>x>>y>>z;
			add(x,z);
			add(y+1,-z);
		}
	}
	return 0;
}

3.区间修改，区间查询

#include<bits/stdc++.h>
using namespace std;
int n,m;
long long a[155000],c1[155000],c2[155000];
long long lowbit(int x){
	return x&-x;
}
void add(int x,int key){
	long long tmp=x;
	while(x<=n){
		c1[x]+=key;
		c2[x]+=(long long)tmp*key;
		x+=lowbit(x);
	}
}
long long getsum(int x){
	long long ans=0,tmp=x;
	while(x){
		ans+=c1[x]*(tmp+1)-c2[x];
		x-=lowbit(x);
	}
	return ans;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		add(i,a[i]-a[i-1]);
	}
	scanf("%d",&m);
    string str;
	int x,y,z;
	for(int i=1;i<=m;i++){
		cin>>str;
		if(str[0]=='S'){
		    cin>>x>>y;
			printf("%lld\n",getsum(y)-getsum(x-1));
		}
		else{
			cin>>x>>y>>z;
			add(x,z);
			add(y+1,-z);
		}
	}
	return 0;
}