题目描述
SERKOI最新推出了一种叫做“免费馅饼”的游戏:游戏在一个舞台上进行。舞台的宽度为W格，天幕的高度为H格，游戏者占一格。开始时游戏者站在舞台的正中央，手里拿着一个托盘。下图为天幕的高度为4格时某一个时刻游戏者接馅饼的情景。
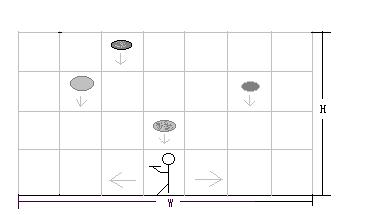
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。
馅饼有很多种，游戏者事先根据自己的口味，对各种馅饼依次打了分。同时，在8-308电脑的遥控下，各种馅饼下落的速度也是不一样的，下落速度以格/秒为单位。
当馅饼在某一秒末恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。
写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。
输入格式
输入文件的第一行是用空格隔开的两个正整数，分别给出了舞台的宽度W（1到99之间的奇数）和高度H（1到100之间的整数）。
接下来依馅饼的初始下落时间顺序给出了所有馅饼的信息。每一行给出了一块馅饼的信息。由四个正整数组成，分别表示了馅饼的初始下落时刻（0到1000秒），水平位置、下落速度（1到100）以及分值。游戏开始时刻为0。从1开始自左向右依次对水平方向的每格编号。
输入文件中同一行相邻两项之间用一个或多个空格隔开。
输出格式
输出文件的第一行给出了一个正整数，表示你的程序所收集的最大分数之和。
样例
样例输入
3 3
0 1 2 5
0 2 1 3
1 2 1 3
1 3 1 4
样例输出
12
思路：重新建图，以馅饼为参考系，馅饼静止，人向上找馅饼。用横坐标表示馅饼下落的位置，纵坐标表示时间（下落高度除以速度）。
状态转移方程：f[i][j]=max(f[i][j],f[i-1][j+k]);//i时刻到达位置j所得的最大分数
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int w,h,n,sum;
int a[N],b[N],c[N],d[N],f[N][N],g[N][N];
int main(){
scanf("%d%d",&w,&h);
h--,n++;//下落高度为h-1
while(cin>>a[n]>>b[n]>>c[n]>>d[n]){
if(h%c[n]==0){
a[n]+=h/c[n];
sum=max(sum,a[n]);//最晚时间
n++;
}
}
n--;//上面多加了1
for(int i=1;i<=n;i++){
g[a[i]][b[i]]+=d[i];//格子代表的分数
}
for(int i=1;i<=sum;i++){
for(int j=1;j<=w;j++){
for(int k=-2;k<=2;k++){
f[i][j]=max(f[i][j],f[i-1][j+k]);
}
f[i][j]+=g[i][j];
}
}
int ans=0;
for(int i=1;i<=w;i++){
ans=max(ans,f[sum][i]);
}
printf("%d",ans);
return 0;
}
