2024年中国科学技术大学少创班一试数学题 Mathematica解答
题目地址
https://app.gaokaozhitongche.com/news/h/E2Jbr6R2
https://www.zizzs.com/gk/shitiku/154255.html
答案地址
https://www.zizzs.com/gk/shitiku/154255_6.html \(\color{red}{\text{看了一下,他给的答案基本都是对的。第一题他没有化简到不可约分数。}}\)
1
从\(\{ 1,2,\cdots ,9 \}\)中选取三个不同的数,从大到小拼成一个三位数\(X\),再从\(\{ 1,2,\cdots, 8 \}\)中选取三个不同的数,从大到小拼成一个三位数\(Y\),求:\(X>Y\)的概率?
Clear["Global`*"];
leftNumbers =
Subsets[Range[9, 1, -1], {3}] //
Map[ToExpression@StringJoin[Map[ToString, #]] &, #] &
rightNumbers =
Subsets[Range[8, 1, -1], {3}] //
Map[ToExpression@StringJoin[Map[ToString, #]] &, #] &
allTuples = Tuples[{leftNumbers, rightNumbers}];
Count[allTuples, _?(#[[1]] > #[[2]] &)]/Length[allTuples]
2
说理题。拿迭代函数系统和极限那一套说清楚就行。
设\(x\geq -1\)且\(x\in \mathbb{R}\),令\(a_1=\sqrt{2x+3},\quad a_{n+1}=\sqrt{2a_n+3}\),试求使数列\(\{a_n\}\)中有无穷多个正整数的\(x\)的全部取值。
x = 3;
RecurrenceTable[{a[n + 1] == Sqrt[2*a[n] + 3], a[1] == Sqrt[2 x + 3]},
a[n], {n, 1, 10}]
要求无穷多个正整数,那么肯定
对递推关系,从后面往前推啊。(这个递推映射又不是【非单射的】,逆函数(只有1种)很容易写啊)
f[x_] := (x^2 - 3)/2;
Table[NestList[f, x, 5], {x, 0, 20}]
\(x=3\)满足要求。
其他看了下,都不符合要求。
可以说明NestList为{3,3,3,3,3...}无穷循坏才是唯一可行的构造。
Clear[x];
Reduce[(x^2 - 3)/2 > x, x, Reals]
(* x < -1 || x > 3 *)
NestList初始元素为0,1,2,3的情况如下,只有NestList初始元素为3的那个可行。
NestList初始元素为1的情况指示我们\(x=1\)或\(x=-1\)可能是可行的?带入正向迭代关系发现实际不行。
NestList初始元素为4,5,6,...的情况都不行啊,
综合以上讨论,只有\(x=3\)满足要求。
3
回忆版试题-版本1
求所有实数\(a\),使得\(|x^2+ax+1|\geq |x+1|\)在\(x\in \mathbb{R}\)上恒成立。
Reduce[Abs[x^2 + a*x + 1] >= Abs[x + 1], x, Reals] //
Column[List @@ #] &
Manipulate[
Plot[Abs[x^2 + a*x + 1] - Abs[x + 1] , {x, -100, 100}], {a, -100,
100}]
如果是该版本试题,Reduce得到答案是\(a=1\)
回忆版试题-版本2
求所有实数\(a\),使得\(|x^2+ax+2|\geq |x+1|\)在\(x\in \mathbb{R}\)上恒成立。
Reduce[Abs[x^2 + a*x + 2] >= Abs[x + 1], x, Reals] //
Column[List @@ #] &
Manipulate[
Plot[Abs[x^2 + a*x + 2] - Abs[x + 1] , {x, -100, 100}], {a, -100,
100}]
如果是该版本试题,Reduce得到答案是\(-1\leq a\leq 2 \sqrt{3}-1\)
4
求所有2024次多项式\(f(x)\),使得\(f(x^2)=f(x)\cdot f(x+2)\)
Clear["Global`*"];
m = 10;
polynomial[x_] := Sum[Subscript[a, n]*x^n, {n, 0, m}];
lhs = polynomial[x^2] == polynomial[x]*polynomial[x + 2] // Expand //
SubtractSides // Part[#, 1] &;
Reduce[CoefficientList[lhs, x] == 0,
Table[Subscript[a, n], {n, 0, m}]] // Column[List @@ #] &
如果要求系数都是整数,也可以做一下。
Clear["Global`*"];
m = 10;
polynomial[x_] := Sum[Subscript[a, n]*x^n, {n, 0, m}];
lhs = polynomial[x^2] == polynomial[x]*polynomial[x + 2] // Expand //
SubtractSides // Part[#, 1] &;
Reduce[CoefficientList[lhs, x] == 0,
Table[Subscript[a, n], {n, 0, m}], Integers] // Column[List @@ #] &
5
复数\(|z_1|=|z_2|=\cdots, =|z_n|=1\),\(z_1+z_2+\cdots +z_n=n-2+ 1i\),其中\(n\geq 2024, n\in \mathbb{Z}\),求\(\Re (z_1)\)的最小值。
首先,\(\Re (z_1)\)取不到\(-1\)。
如果\(\Re (z_1)= -1\),因为\(|z_1|=1\),所以\(z_1=-1\)。那么\(z_2+\cdots +z_n=n-1+ 1i\),满足不了。
尝试转化为优化问题做一下。
n=4的时候最优解可以到-0.931662479 !!这个应该没有什么争议,我用Mathematica和大部分非线性优化求解器都给出这个结果 !!
和别人给出的解析解答案\(\frac{-2 n^2+9 n-\sqrt{4 n-5}-10}{2 \left(n^2-4 n+5\right)}\)也一致 (-2 n^2 + 9 n - 10 - Sqrt[4 n - 5])/(2*(n^2 - 4 n + 5)) /. {n -> 4} // N
| solver \ n= | 4 | 100 | 101 | 2024 |
|---|---|---|---|---|
| Analytical solution | -0.931662 | -0.995829 | -0.995867 | -0.999763 |
| Mathematica | -0.931662479 | -0.995833 | -0.995871 | |
| CONOPT | -0.931662479 | -0.9957903145 | -0.9957903137 | -0.9997414751 |
| LOQO | -0.9316624793 | -0.9995553546 | -1 | -0.9997758303 |
| Ipopt | -0.931662 | -0.995829 | -9.9586691411747985e-01 | 0.0604244 |
| Gurobi | -0.931662479 | -0.9999406579 | ||
| OCTERACT | -0.931662 | -0.995539 | -0.995867 | -0.999763 |
| Knitro | -9.11324841790525e-01 | -9.93555728237769e-01 | 6.86322158040905e-08 | -0.9990907031 |
本题答案(\(n=2024\)的情况)应该是-0.999763,OCTERACT在\(n=2024\)给出的结果也是-0.999763。
看了一下OCTERACT对于其他\(n\)的结果,可以说OCTERACT给出的数值结果是和此解析结果最接近的。
Mathematica求解优化问题
Clear["Global`*"];
ansList = {};
For[n = 3, n <= 20, n++,(*Change this value to any positive integer*)
xSymbols = Array[Symbol["x" <> ToString@#] &, n];
ySymbols = Array[Symbol["y" <> ToString@#] &, n];
(*Generating the constraints for each x_i and y_i to be on the unit \
circle*)
unitCircleConstraints =
Table[xSymbols[[i]]^2 + ySymbols[[i]]^2 == 1, {i, 1, n}];
(*Including other constraints in your original problem*)
otherConstraints = {Total[xSymbols] == n - 2,
Total[ySymbols] == 1};
(*Combining all constraints*)
constraints = Join[unitCircleConstraints, otherConstraints];
(*Solving the minimization problem*)
solution =
NMinimize[{First[xSymbols], constraints}, Join[xSymbols, ySymbols]];
AppendTo[ansList, solution[[1]]];
Print["n=", n, " sol=", solution];];
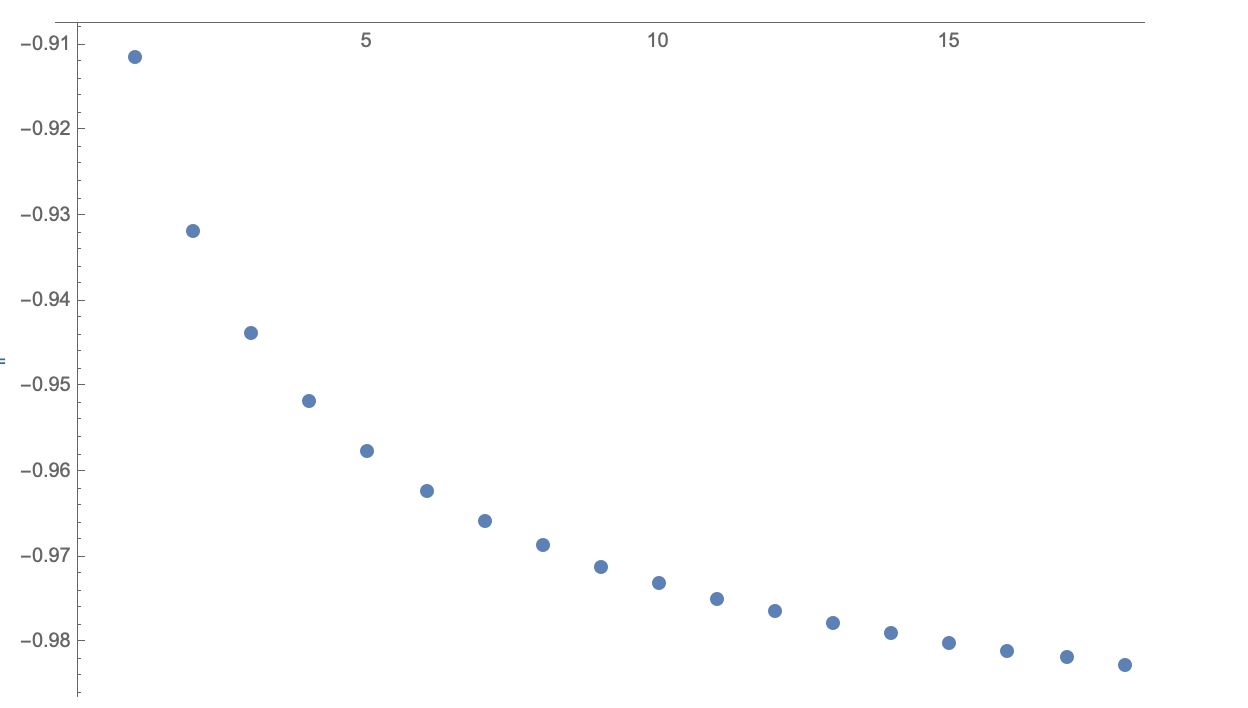
ListPlot[ansList]
OCTERACT求解优化问题
nco问题求解器我个人建议使用OCTERACT。
可以写一个AMPL .mod文件,在NEOS的OCTERACT/AMPL页面提交一下
param n := 4;
# Define variables
var x {i in 1..n} >= -1, <= 1; # Variables x_i bounded by the circle's radius
var y {i in 1..n} >= -1, <= 1; # Variables y_i bounded by the circle's radius
# Define constraints
s.t. UnitCircle {i in 1..n}:
x[i]^2 + y[i]^2 = 1; # Each (x_i, y_i) must lie on the unit circle
s.t. SumX:
sum {i in 1..n} x[i] = n - 2; # Additional constraint on sum of x_i
s.t. SumY:
sum {i in 1..n} y[i] = 1; # Additional constraint on sum of y_i
# Objective function to minimize the first x variable
minimize Objective:
x[1];
# Solver options (if available and applicable)
option solver_options 'BarHomogeneous=1';
option gurobi_options "NonConvex=2";
# Solve the problem
solve;
# Displaying the results
display x, y;
附录 绘制m个随机单位模复数的和(随机游走)
(*Define the complex numbers z1,z2,z3*)
z1[\[Theta]1_] := Exp[I \[Theta]1];
z2[\[Theta]2_] := Exp[I \[Theta]2];
z3[\[Theta]3_] := Exp[I \[Theta]3];
(*Function to sum the complex numbers*)
totalZ[\[Theta]1_, \[Theta]2_, \[Theta]3_] :=
z1[\[Theta]1] + z2[\[Theta]2];
(*Generate a 3D plot to visualize the region generated by the sum*)
\
ParametricPlot[
ReIm[totalZ[\[Theta]1, \[Theta]2, \[Theta]3]], {\[Theta]1, 0,
2 Pi}, {\[Theta]2, 0, 2 Pi}, PlotRange -> All,
AxesLabel -> {"Re", "Im"}, Mesh -> None, PlotPoints -> 50,
PlotLabel -> "Visualization of the Sum z1 + z2"]
ParametricPlot最多就支持2个自变量?这里MonteCarlo画一下
(*Number of random samples*)n = 10000;
m = 3; (* Number of vectors*)
(*Generate random angles*)
thetaList =
Array[RandomReal[{0, 2 Pi}, n] &, m];
(*Calculate z1+z2+z3*)
sums = Total[Exp[I #] & /@ thetaList];
(*Plot the results*)
ListPlot[Through[{Re, Im}[#]] & /@ sums,
AspectRatio -> 1, PlotRange -> All, PlotStyle -> PointSize[Small],
PlotLabels -> {"Real", "Imaginary"}]


