2023年北京大学强基计划 部分数学试题Mathematica解答
第4、9题我还没找到可靠的答案。
试题地址
全网首发！2023年北京大学强基计划笔试数学试题（全！） - ADU的小窝的文章 - 知乎 转自数理迷津
https://zhuanlan.zhihu.com/p/640415621
1
emmm比如说三个点的实部，虚部分别是：
有理数，无理数
无理数，有理数
有理数，无理数
有理数+无理数+有理数 可以是无理数
无理数+有理数+无理数 可以是有理数或者无理数
比如说三个点的实部，虚部分别是：
有理数，无理数
有理数，无理数
有理数，无理数
有理数+有理数+有理数 可以是有理数
无理数+无理数+无理数 可以是有理数或者无理数
剩下的情况都和以上类似，用对称性就行。
选择\(\color{red}{\text{D}}\)
2
在\([0,2\pi]\)的实数解有\(\color{red}{\text{0}}\)个。
expr = 1 + Cos[x] + I*Sin[x] - Cos[2 x] - I*Sin[2 x] + Cos[3 x] +
I*Sin[3 x];
NSolve[expr == 0, x]
\[\{\{x\to \fbox{$1. ((3.14159\, +0.609378 i)+6.28319 c_1)\text{ if }c_1\in \mathbb{Z}$}\},\{x\to \fbox{$1. ((-0.965359-0.304689 i)+6.28319 c_1)\text{ if }c_1\in \mathbb{Z}$}\},\{x\to \fbox{$1. ((0.965359\, -0.304689 i)+6.28319 c_1)\text{ if }c_1\in \mathbb{Z}$}\}\}
\]
expr = 1 + Cos[x] + I*Sin[x] - Cos[2 x] - I*Sin[2 x] + Cos[3 x] +
I*Sin[3 x];
imaginaryPart = Assuming[x~Element~Reals, Im@expr // FullSimplify];
realPart = Assuming[x~Element~Reals, Re@expr // FullSimplify];
Solve[realPart == 0 && imaginaryPart == 0 && x >= 0 && x <= 2*Pi, x]
\[\{\}
\]
是不是回忆版试题记错题目了？？？
3
RecurrenceTable[{a[n] == a[n - 1]^2 - 2, a[1] == 5/2},
a, {n, 1, 10}] // Map[Floor[#]~Mod~7 &, #] &
答案是\(\color{red}{\text{2}}\)
4
不会。
5
f[list_] := list~Append~Max@list;
exprs = f[{Sin@x, Cos@x, -x/Pi + 1}];
Plot[exprs, {x, 0, Pi}, PlotLegends -> exprs]
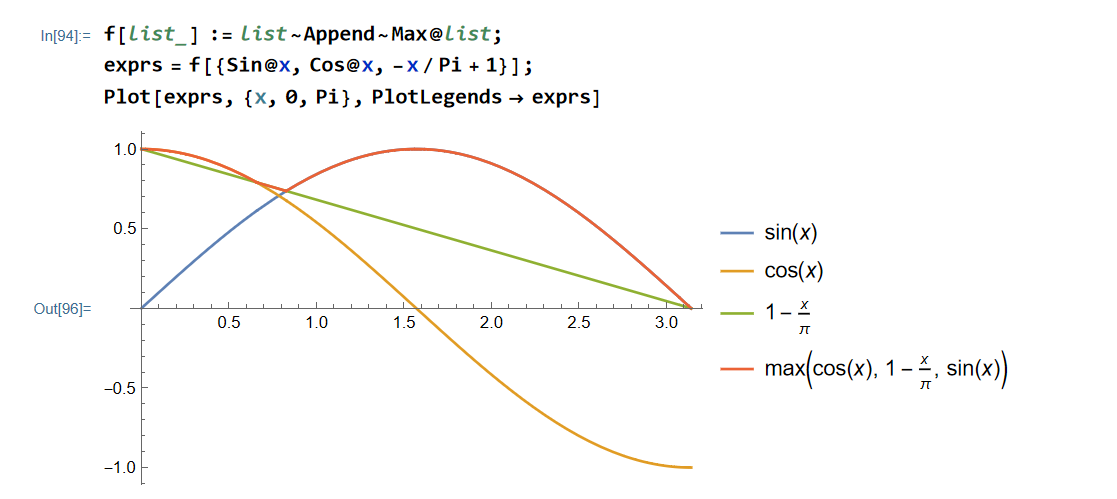
画图就行，答案是Max[Cos[0], Sin[Pi/2]] 答案是\(\color{red}{\text{1}}\)
6
nmax = 50;
lst = Table[{x (y + 1)/(x - 1), y (z + 1)/(y - 1),
z (x + 1)/(z - 1)}, {x, 2, nmax}, {y, 2, nmax}, {z, 2, nmax}] //
Flatten[#, 2] & // Select[#, AllTrue[#, IntegerQ] &] &;
products = lst // Map[Times @@ # &, #] &
Max@products - Min@products
所有解就这些
\[\left(
\begin{array}{ccc}
6 & 6 & 6 \\
6 & 10 & 4 \\
10 & 4 & 6 \\
14 & 6 & 4 \\
6 & 6 & 6 \\
6 & 9 & 5 \\
9 & 5 & 6 \\
12 & 7 & 5 \\
4 & 6 & 10 \\
4 & 14 & 6 \\
12 & 8 & 6 \\
5 & 6 & 9 \\
5 & 12 & 7 \\
6 & 4 & 14 \\
6 & 12 & 8 \\
7 & 5 & 12 \\
14 & 11 & 9 \\
8 & 6 & 12 \\
9 & 14 & 11 \\
11 & 9 & 14 \\
\end{array}
\right)
\]
答案是\(\color{red}{1170}\)
7
NSolve[24 x^5 - 15 x^4 + 40 x^3 - 30 x^2 + 120 x + 1 == 0, x]
\[\{\{x\to -0.694033-1.30844 i\},\{x\to -0.694033+1.30844 i\},\{x\to -0.00831585\},\{x\to 1.01069\, -1.12363 i\},\{x\to 1.01069\, +1.12363 i\}\}
\]
\(\color{red}{\text{1}}\)个实数根。
8
vectors = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
step[n_, vectors_] := Table[1/4^n*v, {v, vectors}];
t = Tuples[Table[step[n, vectors], {n, 1, 10}]] // Map[Total, #] & ;
t // Length (*1048576*)
t // Union // Length (*1048576*)
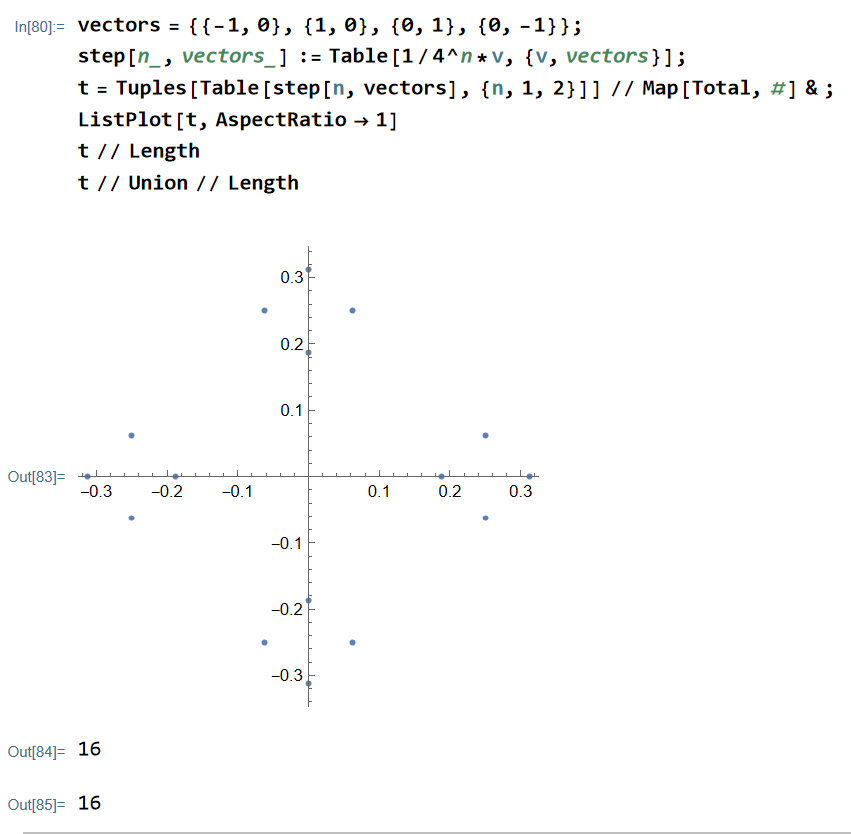
这是第3天(\(n=3\))的分布，有\(16=4^2\)个不同的位置。
我猜，
第2023天(\(n=2023\))的分布，有\(\color{red}{{4^{2022}}}\)个不同的位置。
9
Clear["Global`*"];
p = (a + b + c)/2;
S = Sqrt[p*(p - a)*(p - b)*(p - c)];
expr1 = (a^2*(2 S/a)^2 == a^2*(2^2) // FullSimplify // Expand);
expr2 = (4 b^2*(2 S/b)^2 == 4 b^2*(4^2) // FullSimplify // Expand);
FindMaximum[{S/p,
expr1 && expr2 && a + b > c && b + c > a && a + c > b && a > 0 &&
b > 0 && c > 0}, {a, 4}, {b, 5}, {c, 5}, AccuracyGoal -> 8,
PrecisionGoal -> 6]
FindMaximum[{S/p,
expr1 && expr2 && a + b > c && b + c > a && a + c > b && a > 0 &&
b > 0 && c > 0}, {a, 2}, {b, 2}, {c, 2}]
FindMinimum[{S/p,
expr1 && expr2 && a + b > c && b + c > a && a + c > b && a > 0 &&
b > 0 && c > 0}, {a, 2}, {b, 3}, {c, 4}]
FindMinimum是找某个点附近局部最小值的，
FindMaximum是找某个点附近局部最大值的。
这题我没找到可靠的答案。
10
range = Range[1, 10];
sets = Subsets[range, {3}];
gcd[list_] := GCD@list == 1;
coprimeSets = Select[sets, gcd];
Length[coprimeSets]
\[\color{red}{\text{109}}
\]
11
(20000/20) // FactorInteger
\[2^3 \cdot 5^3
\]
\((3+1)\cdot(3+1)\) 是 \(16\)
答案是\(\color{red}{16\times 15 \times 14}\)
12
如果你和我一样不会构造只会暴力的话，可以建模，就是在边权都为1的图中求最大匹配数。
(*集合 U={1,2,...,366}*)
U = Range[366];
(*寻找顶点对，使得它们的和是17的倍数*)
edges = Select[Subsets[U, {2}], Mod[Total[#], 17] == 0 &];
(*转换成图的边*)
edgesInGraph = UndirectedEdge @@@ edges;
(*创建图*)
G = Graph[U, edgesInGraph];
(*找到最大匹配*)
maxMatching = FindIndependentEdgeSet[G];
(*最大匹配数*)
maxMatchingNumber = Length[maxMatching]
maxMatchingNumber
\[\color{red}{\text{179}}
\]
13
a = {-1, 0};
b = {1, 0};
c = {Cos[t], Sin[t]};
d = c + (c - a)/Norm[c - a, 2]*(3*Norm[c - b, 2]);
e = {4, 5};
ListPlot[Table[d, {t, -2 Pi, 2 Pi, 0.01}]]
deDistance = Norm[d - e, 2];
Plot[deDistance, {t, -2 Pi, 2 Pi}]
FindMinimum[deDistance, {t, 2}]
FindMaximum[deDistance, {t, 2.6}]
%[[1]]*%%[[1]]
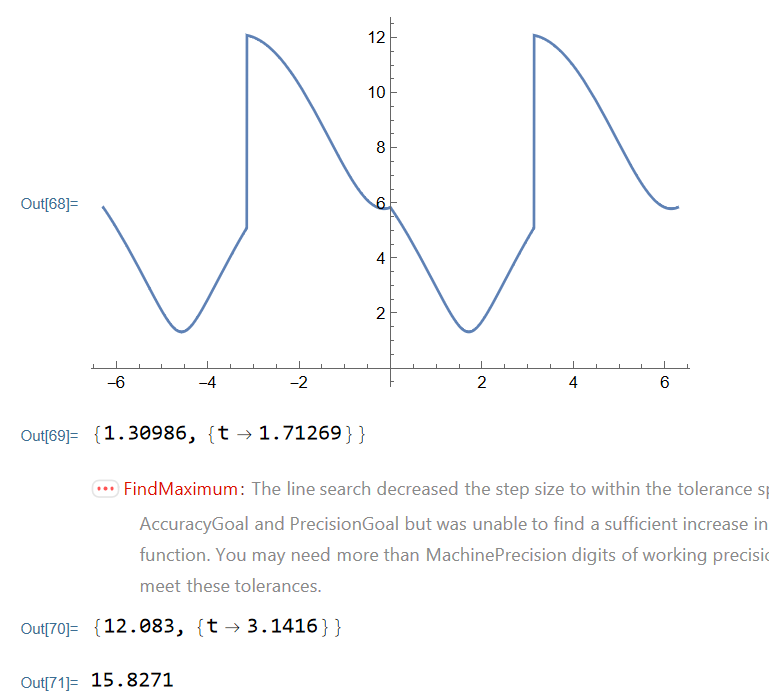
数值结果大概是\(\color{red}{\text{15.8271}}\)
14
Table[Floor[n^2/2023], {n, 1, 2023, 1}] // Union // Length
\[\color{red}{\text{1518}}
\]
15
cnt = 0;
For[a = 1, a <= 98, a++,
For[b = a + 1, b <= 99, b++,
For[c = b + 1, c <= 100, c++,
For[d = c + 1, d <= 101, d++,
If[Mod[a + b + c + d, 101] == 0, cnt = cnt + 1]]]]];
Print["cnt=", cnt];
\[\color{red}{\text{40425}}
\]
16
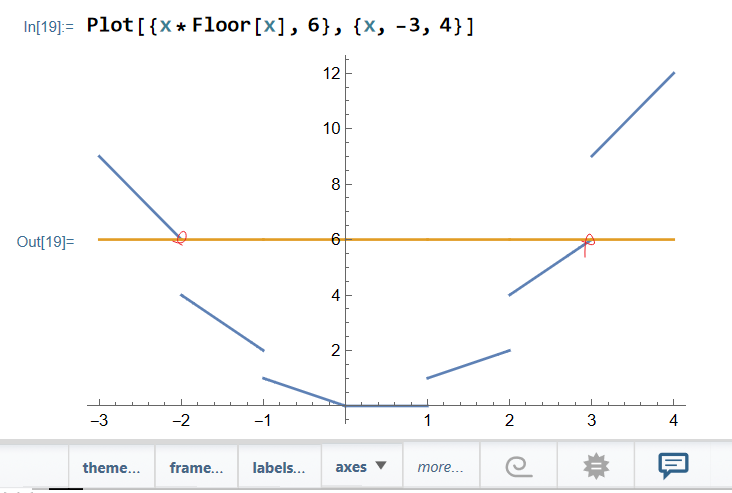
这2个正好是空心点。
方程\(x[x]=6\)共有\(\color{red}{\text{0}}\)个解。
17
Clear["Global`*"];
R[n_] := Sum[n~Mod~mod, {mod, Range[2, 10, 1]}];
Table[R[n] - R[n + 1], {n, 10, 99, 1}] // Count[#, 0] &
\[\color{red}{\text{2 个}}
\]
18
expr = (x + y)^2 + (y - z)^2 + (z - t)^2 + (t - x)^2 // Expand
perms = Permutations[{a, b, c, d}];
results =
Table[expr /. {x -> perm[[1]], y -> perm[[2]], z -> perm[[3]],
t -> perm[[4]]}, {perm, perms}] // Union // Length
\[\color{red}{\text{12}}
\]
去重后就这\(12\)种
\[\begin{align*}
& 2 a^2+2 a c-2 a d+2 b^2-2 b c-2 b d+2 c^2+2 d^2, \\
& 2 a^2-2 a c-2 a d+2 b^2+2 b c-2 b d+2 c^2+2 d^2, \\
& 2 a^2-2 a c+2 a d+2 b^2-2 b c-2 b d+2 c^2+2 d^2, \\
& 2 a^2-2 a c-2 a d+2 b^2-2 b c+2 b d+2 c^2+2 d^2, \\
& 2 a^2+2 a b-2 a d+2 b^2-2 b c+2 c^2-2 c d+2 d^2, \\
& 2 a^2-2 a b-2 a d+2 b^2+2 b c+2 c^2-2 c d+2 d^2, \\
& 2 a^2-2 a b+2 a d+2 b^2-2 b c+2 c^2-2 c d+2 d^2, \\
& 2 a^2+2 a b-2 a c+2 b^2-2 b d+2 c^2-2 c d+2 d^2, \\
& 2 a^2-2 a b+2 a c+2 b^2-2 b d+2 c^2-2 c d+2 d^2, \\
& 2 a^2-2 a b-2 a c+2 b^2+2 b d+2 c^2-2 c d+2 d^2, \\
& 2 a^2-2 a b-2 a d+2 b^2-2 b c+2 c^2+2 c d+2 d^2, \\
& 2 a^2-2 a b-2 a c+2 b^2-2 b d+2 c^2+2 c d+2 d^2
\end{align*}
\]
19
// how to build and run?
// cargo build --release
// cargo run --release
fn main() {
let mut min_diff = std::i32::MAX; // 初始化最小差值为最大整数
let mut max_sum = 0; // 初始化最大和为0
// 这里我们假设了 x1 的上限是 30，你可以根据需要调整这个值
for x1 in 1..30 {
for x2 in x1+1..30 {
for x3 in x2+1..30 {
for x4 in x3+1..30 {
for x5 in x4+1..30 {
for x6 in x5+1..30 {
for x7 in x6+1..30 {
for x8 in x7+1..30 {
for x9 in x8+1..30 {
// 检查 x1 到 x9 的和是否等于220
if x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 == 220 {
// 如果 x1 到 x5 的和大于当前的最大和，则更新最大和
if x1 + x2 + x3 + x4 + x5 > max_sum {
max_sum = x1 + x2 + x3 + x4 + x5;
}
}
}
}
}
}
}
}
}
}
}
println!("Max x1~x5 sum: {}", max_sum);
for x1 in 1..30 {
for x2 in x1+1..30 {
for x3 in x2+1..30 {
for x4 in x3+1..30 {
for x5 in x4+1..30 {
for x6 in x5+1..30 {
for x7 in x6+1..30 {
for x8 in x7+1..30 {
for x9 in x8+1..30 {
// 检查 x1 到 x9 的和是否等于220
if x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 == 220 {
if x1 + x2 + x3 + x4 + x5 == max_sum {
min_diff = std::cmp::min(min_diff,x9-x1);
}
}
}
}
}
}
}
}
}
}
}
println!("Min (x9-x1) when (x1~x5 sum=={}): {}", max_sum, min_diff);
}
Max x1~x5 sum: 110
Min (x9-x1) when (x1~x5 sum==110): 9
答案是\(\color{red}{9}\)
20
经典的计数问题。
如果限定是正多边形的话，区域数目序列是A007678。论文可以看这个
如果是一般形状的凸多边形(且尽可能让区域数目多)的话，区域数目序列是A006522。论文可以看这个
Table[Binomial[n, 4] + Binomial[n - 1, 2], {n, 1, 10}]
\[\{0,0,1,4,11,25,50,91,154,246\}
\]
答案是\(\color{red}{\text{246}}\)
