【读书笔记】Parking Function

我太笨了，很多看不懂

目录

• 13.1 引言
• 13.2 Parking functions和有标记的树
  • 13.2.1 有标记的树的序列化：Labeled trees with Prufer code
  • 13.2.2 Inversions of labeled trees
  • 13.2.3 图搜索算法
  • 13.2.4 External activity of labeled trees
  • 13.2.5 稀疏连通图
• 13.3 Parking functions面面观
  • 13.3.1 哈希和线性探针
  • 13.3.2 Latice of noncrossing partitions
  • 13.3.3 超平面排布 hyperplane arrangements
  • 13.3.4 在优先队列中允许的输入-输出对
  • 13.3.5 parking functions的两个变体
• 13.4 广义的Parking functions
  • 13.4.1 u-parking functions
  • 13.4.2 parking polytope
  • 13.4.3 Goncarov polynomials理论
  • 13.4.4 经典parking functions
• 13.5 和图关联的Parking functions
  • 13.5.1 G-parking functions
  • 13.5.2 阿贝尔沙堆模型 Abelian sandpile model
  • 13.5.3 Multiparking functions, graph searching, and the Tutte polynomial
• 13.6 最后的一些备注

13.1 引言

关于Parking Function，这是一个简短的35页介绍性质的PDF

长度为\(n\)的parking function数目是\((n+1)^{n-1}\)
\(n+1\)个节点的有标记无根树的数目也是\((n+1)^{n-1}\)

parking function定义有很多种，

(2,0,1,0,1,3,6,0)就是一个Parking funciton
按照非降序重排后是(0,0,0,1,1,2,3,6),满足\(0 \leq a_{(i)}<i\ \text{ for }\ 1\leq i\leq n\)
0<=0<1
0<=0<2
0<=0<3
0<=1<4
0<=1<5
0<=2<6
0<=3<7
0<=6<8

另外一种是用停车场景来定义
有8辆车(1号到8号)，有8个车位(0号到7号)，钟爱的车位被抢，从钟爱的车位+1开始往后找可行的车位
1号车钟爱2号位
2号车钟爱0号位
3号车钟爱1号位
4号车钟爱0号位
5号车钟爱1号位
6号车钟爱3号位
7号车钟爱6号位
8号车钟爱0号位

所以，1号车会停在2号位，2号车会停在0号位，3号车会停在1号位，4号车会停在3号位，5号车会停在4号位，6号车会停在5号位，7号车会停在6号位，8号车会停在7号位

13.2 Parking functions和有标记的树

13.2.1 有标记的树的序列化：Labeled trees with Prufer code

先介绍了Prufer code这一序列化的方式

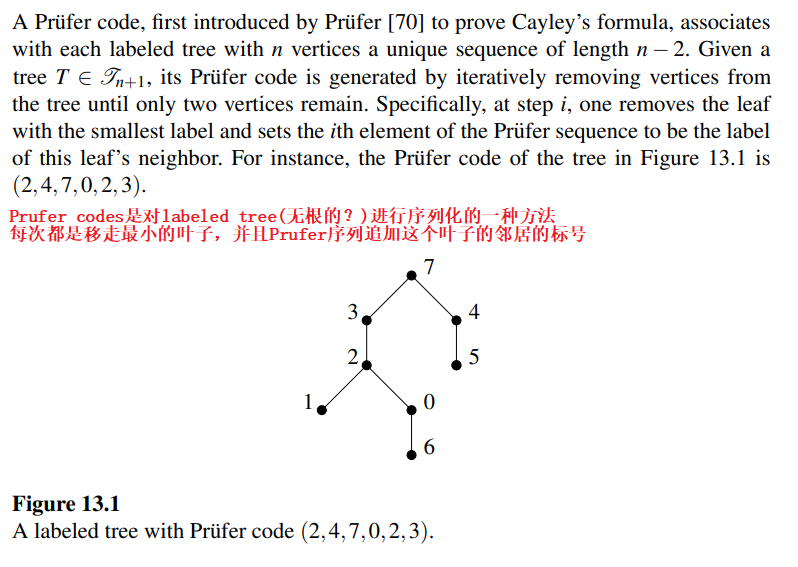
介绍了这个双射

序列a和序列c互相转换的算法如下

PruferCode2ParkinngFunction[c_List] := With[{n = Length@c + 1},
  cAccumulate = Accumulate@c;
  h = {0}~Join~(cAccumulate // Map[Mod[#, n + 1] &, #] &);
  r = BinCounts[h, {0, n + 1, 1}];
  rAccumulate = Accumulate@r;
  R = Table[rAccumulate[[j]] - j, {j, 1, n + 1}];
  d = Ordering[R, 1] - 1(*找到最小值位置,-1做下标从1/0开始的修正*);
  a1 = n - d;
  a = a1~Join~(cAccumulate // Map[Mod[# + a1, n + 1] &, #] & // 
      Flatten)
  ]

PruferCode2ParkinngFunction[{2, 4, 7, 0, 2, 5}]


(*PruferCode转成对应的ParkingFunction，结果是{4, 6, 2, 1, 1, 3, 0}*)




ParkingFunction2PruferCode[a_List] := With[{n = Length@a},
  Differences[a] // Map[Mod[#, n + 1] &, #] &
  ]

ParkingFunction2PruferCode[{4, 6, 2, 1, 1, 3, 0}]

(*ParkingFunction转成对应的PruferCode，结果是{2, 4, 7, 0, 2, 5}*)

介绍了一个q-analog

Corollary 13.2.4 The equality

\[\sum_{\alpha \in \mathscr{P} \mathscr{K}_{n}} q^{\left|\left\{i: a_{i}=a_{i+1}\right\}\right|}=(q+n)^{n-1} . \]

holds, where \(|S|\) is the cardinality of a set \(S\).

举例，对于\(n=3\)
n = 3 : 000 001 010 100 002 020 200 011
101 110 012 021 102 120 201 210

\[q^2+q^1+q^0+q^1+q^1+q^0+q^1+q^1+q^0+q^1+q^0+q^0+q^0+q^0+q^0+q^0=q^2+6q+9=(q+3)^2 \]

13.2.2 Inversions of labeled trees

不仅仅是两个计数的分布相等，
还可以构造一个双射

举例

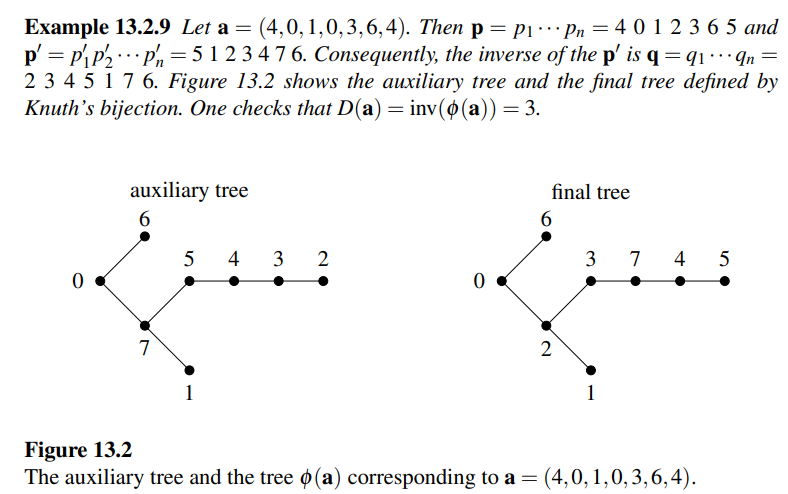
13.2.3 图搜索算法

定义了 specification 就是类似于Python里的Counter
定义了 order permutation \(σ_i\) is the position of the entry \(a_i\) in the non-decreasing rearrange

举例\(\mathbf{a}=\left(\begin{array}{llllllll} 2 & 0 & 3 & 0 & 4 & 8 & 1 & 5 \end{array}\right)\)

非降低排序后是\(\mathbf{a_{sorted}}=(0,0,1,2,3,4,4,5,8)\)

specification \(\vec{r}(\mathbf{a})=(2,1,1,1,2,1,0,0,1)\) （书这里写错了？）
order permutation是\(\sigma(\alpha)=415269387\)   因为\(a_1=2\)在\(\mathbf{a_{sorted}}\)的第4个位置，所以你追加4；\(a_2=0\)在\(\mathbf{a_{sorted}}\)的第1个位置，所以你追加1；\(a_3=3\)在\(\mathbf{a_{sorted}}\)的第5个位置，所以你追加5；\(a_4=0\)在\(\mathbf{a_{sorted}}\)的第2个位置(第1个位置已经占用)，所以你追加2；。。。

permutation 和 它的(specification,order permutation) 相互唯一确定

13.2.4 External activity of labeled trees

13.2.5 稀疏连通图

13.3 Parking functions面面观

13.3.1 哈希和线性探针

13.3.2 Latice of noncrossing partitions

13.3.3 超平面排布 hyperplane arrangements

13.3.4 在优先队列中允许的输入-输出对

13.3.5 parking functions的两个变体

13.4 广义的Parking functions

13.4.1 u-parking functions

13.4.2 parking polytope

13.4.3 Goncarov polynomials理论

The Goncarov polynomials \(g_n(x;a_0,a_1,...,a_{n-1})\)有如下性质

13.4.4 经典parking functions

13.5 和图关联的Parking functions

13.5.1 G-parking functions

13.5.2 阿贝尔沙堆模型 Abelian sandpile model

13.5.3 Multiparking functions, graph searching, and the Tutte polynomial

13.6 最后的一些备注

提到了Macdonald多项式（麦克唐纳多项式），和parking functions关联很大 ————（过于前沿orz）

labeled dyck paths和parking function有个双射，举例如下

 

书用的是Handbook of Enumerative Combinatorics by Miklos Bona

资料来自网络