几种常见的概率分布及其一些统计量（转载及补充）

2018年存在我手机里的这2张图片
图片来自这篇博客

图片

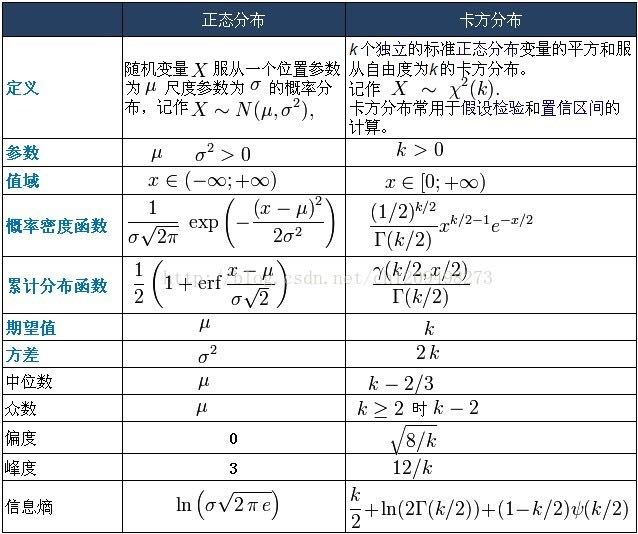
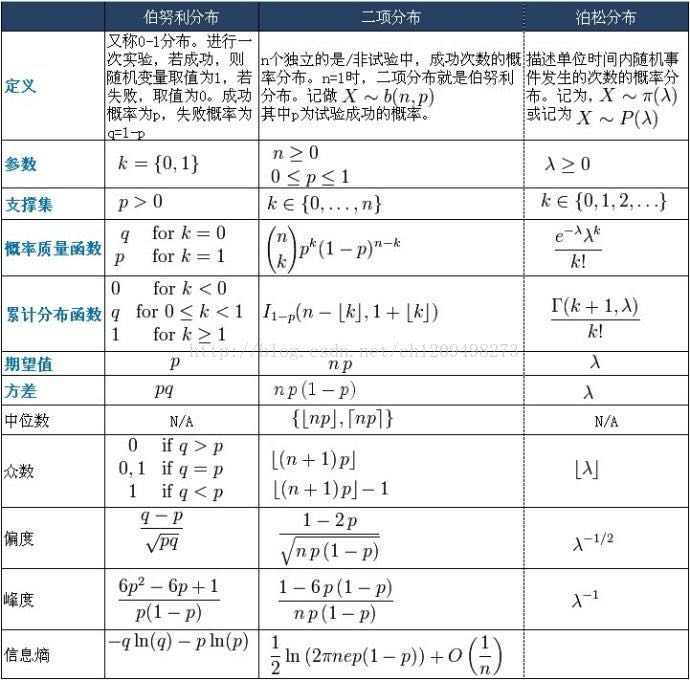
一些概念

偏度

皮尔逊偏度系数把偏度定义为

{\tilde{μ}}_{3} = E [{(\frac{X - μ}{σ})}^{3}] = \frac{μ_{3}}{σ^{3}} = \frac{E [(X - μ)^{3}]}{{(E [(X - μ)^{2}])}^{3 / 2}} = \frac{κ_{3}}{κ_{2}^{3 / 2}}

$\tilde{\mu}_{3}=\mathrm{E}\left[\left(\frac{X-\mu}{\sigma}\right)^{3}\right]=\frac{\mu_{3}}{\sigma^{3}}=\frac{\mathrm{E}\left[(X-\mu)^{3}\right]}{\left(\mathrm{E}\left[(X-\mu)^{2}\right]\right)^{3 / 2}}=\frac{\kappa_{3}}{\kappa_{2}^{3 / 2}}$

其中 $\kappa_i$ 是累积量
Skewness indicates the direction and relative magnitude of a distribution's deviation from the normal distribution.

中位数 median

PDF曲线面积一半对应的位置

众数 mode

PDF曲线最大值对应的位置

峰度

皮尔逊峰度系数把峰度(kurtosis)定义为

Kurt [X] = E [{(\frac{X - μ}{σ})}^{4}] = \frac{E [(X - μ)^{4}]}{{(E [(X - μ)^{2}])}^{2}} = \frac{μ_{4}}{σ^{4}}

$\operatorname{Kurt}[X]=\mathrm{E}\left[\left(\frac{X-\mu}{\sigma}\right)^{4}\right]=\frac{\mathrm{E}\left[(X-\mu)^{4}\right]}{\left(\mathrm{E}\left[(X-\mu)^{2}\right]\right)^{2}}=\frac{\mu_{4}}{\sigma^{4}}$

峰度是描述总体中所有取值分布形态陡缓程度的统计量。这个统计量需要与正态分布相比较，峰度为3表示该总体数据分布与正态分布的陡缓程度相同；峰度大于3表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；峰度小于3表示该总体数据分布与正态分布相比较为平坦，为平顶峰。

信息熵

连续分布（应该叫做差熵）

h (X) = - \int p (x) log (p (x)) d x

$h(X)=-\int p(x)\text{log}(p(x))dx$

离散分布

H (X) = - \sum_{i} [p_{i} (x) log (p_{i} (x))]

$H(X)=-\sum\limits_{i}[p_i(x)\text{log}(p_i(x))]$

PDF

probability density function概率密度函数 $f(x)$

或者叫 probability mass function

CDF

累计分布函数 cumulative distribution function

F (x) = P (X \leq x)

$F(x)=P(X\leq x )$

the survivor function

S (x) = P (X \geq x)

$S(x)=P(X\geq x)$

the hazard function

h (x) = \frac{f (x)}{S (x)}

$h(x)=\frac{f(x)}{S(x)}$

the cumulative hazard funciton

符号别和信息熵弄混了。。。

H (x) = - \ln S (x)

$H(x)=-\ln S(x)$

the moment generating function矩生成函数 MGF

随机变量 $X$ 的矩生成函数定义为

M (t) = E [e^{t X}]

$M(t)=E[e^{tX}]$

矩生成函数可用于计算分布的矩：

\begin{aligned} M_{X} (t) = E (e^{t X}) & = 1 + t E (X) + \frac{t^{2} E (X^{2})}{2!} + \frac{t^{3} E (X^{3})}{3!} + \dots + \frac{t^{n} E (X^{n})}{n!} + \dots \\ = 1 + t m_{1} + \frac{t^{2} m_{2}}{2!} + \frac{t^{3} m_{3}}{3!} + \dots + \frac{t^{n} m_{n}}{n!} + \dots \end{aligned}

$\begin{aligned} M_{X}(t)=\mathrm{E}\left(e^{t X}\right) &=1+t \mathrm{E}(X)+\frac{t^{2} \mathrm{E}\left(X^{2}\right)}{2 !}+\frac{t^{3} \mathrm{E}\left(X^{3}\right)}{3 !}+\cdots+\frac{t^{n} \mathrm{E}\left(X^{n}\right)}{n !}+\cdots \\ &=1+t m_{1}+\frac{t^{2} m_{2}}{2 !}+\frac{t^{3} m_{3}}{3 !}+\cdots+\frac{t^{n} m_{n}}{n !}+\cdots \end{aligned}$

the characteristic function特征函数 CF

随机变量 $X$ 的特征函数定义为

Φ (t) = E [e^{j t X}]

$\Phi(t)=E[e^{jtX}]$

在概率论和统计学中，任何实值随机变量的特征函数完全定义了其概率分布。

{\begin{cases} φ_{X} : R \to C \\ φ_{X} (t) = E [e^{i t X}] = \int_{R} e^{i t x} d F_{X} (x) = \int_{R} e^{i t x} f_{X} (x) d x \end{cases}

$\left\{\begin{array}{l} \varphi_{X}: \mathbb{R} \rightarrow \mathbb{C} \\ \varphi_{X}(t)=\mathrm{E}\left[e^{i t X}\right]=\int_{\mathbb{R}} e^{i t x} d F_{X}(x)=\int_{\mathbb{R}} e^{i t x} f_{X}(x) d x \end{array}\right.$

f_{X} (x) = \frac{1}{2 π} \int_{R} φ_{X} (t) e^{- j t x} d t

$f_{X}(x)=\frac{1}{2\pi}\int_{\mathbb{R}}\varphi_X(t)e^{-jtx}dt$

利用随机变量X的特征函数CF求X的k阶矩

E [X^{k}] = i^{- k} φ_{X}^{(k)} (0)

$\mathrm{E}\left[X^{k}\right]=i^{-k} \varphi_{X}^{(k)}(0)$

E [X^{1}] = i^{- 1} φ_{X}^{(1)} (0) = - j φ_{X}^{(1)} (0)

$\mathrm{E}\left[X^{1}\right]=i^{-1} \varphi_{X}^{(1)}(0)=-j \varphi_{X}^{(1)}(0)$

E [X^{2}] = i^{- 2} φ_{X}^{(2)} (0) = - φ_{X}^{(2)} (0)

$\mathrm{E}\left[X^{2}\right]=i^{-2} \varphi_{X}^{(2)}(0)=-\varphi_{X}^{(2)}(0)$

例子

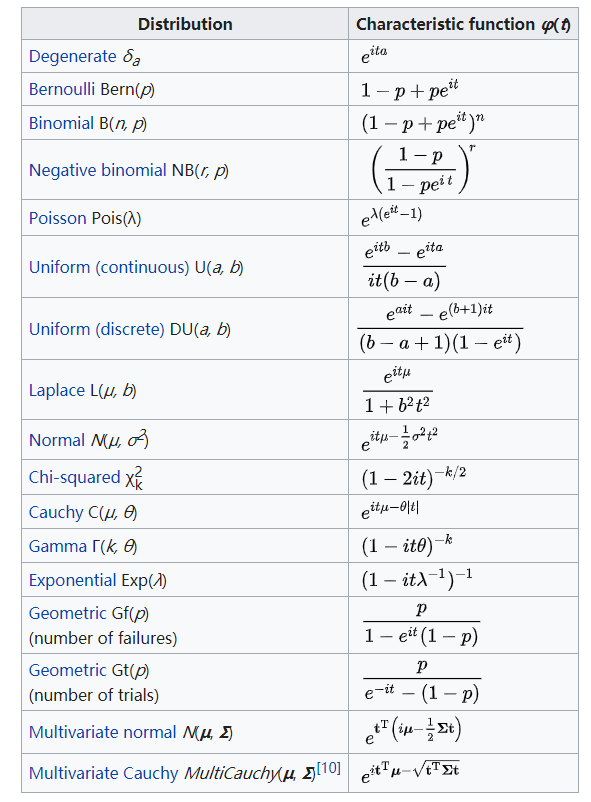
这个积分建议背一下

\int_{- \infty}^{\infty} e^{i t x} \frac{1}{\sqrt{2 π} σ} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}} d x = e^{i t μ - \frac{1}{2} σ^{2} t^{2}}

$\int\limits_{-\infty}^{\infty} e^{i t x} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} d x=e^{i t \mu-\frac{1}{2} \sigma^{2} t^{2}}$

inverse distribution

逆分布是随机变量的倒数服从的分布
让随机变量 $Y=\frac{1}{X}$

G (y) = \Pr (Y \leq y) = \Pr (X \geq \frac{1}{y}) = 1 - \Pr (X < \frac{1}{y}) = 1 - F (\frac{1}{y})

$G(y)=\operatorname{Pr}(Y \leq y)=\operatorname{Pr}\left(X \geq \frac{1}{y}\right)=1-\operatorname{Pr}\left(X<\frac{1}{y}\right)=1-F\left(\frac{1}{y}\right)$

式子两边再对 $y$ 求导

g (y) = \frac{1}{y^{2}} f (\frac{1}{y})

$g(y)=\frac{1}{y^{2}} f\left(\frac{1}{y}\right)$

正交、不相关、独立

首先拿随机变量举例子

从上往下分别是：正交、不相关、独立

E [X Y] = 0 C o v [X, Y] = E [X Y] - E [X] E [Y] = 0 i.e. ρ_{X Y} = \frac{C o v [X, Y]}{σ_{X} σ_{Y}} = 0 p_{X Y} (x, y) = p_{X} (x) p_{Y} (y)

$E[XY]=0\\ Cov[X,Y]=E[XY]-E[X]E[Y]=0\quad \text{i.e.} \quad \rho_{XY}=\frac{Cov[X,Y]}{\sigma_X\sigma_Y}=0\\ p_{XY}(x,y)=p_X(x)p_Y(y)$

下面拿随机过程为例子

常见的概率分布总结及它们间的联系

http://www.math.wm.edu/~leemis/chart/UDR/UDR.html

APPL: A Probability Programming Language

http://www.math.wm.edu/~leemis/2001amstat.pdf
http://mtholyoke.edu/~mpeterso/classes/math342/appl.html

posted @ 2020-11-16 09:25 yhm138 阅读(2262) 评论(0) 编辑收藏举报

yhm138

HelloWorld！

yhm138

几种常见的概率分布及其一些统计量（转载及补充）

图片

一些概念