【公式编辑测试】三角形中线垂线角平分线长度公式
喜闻乐见的公式编辑环节
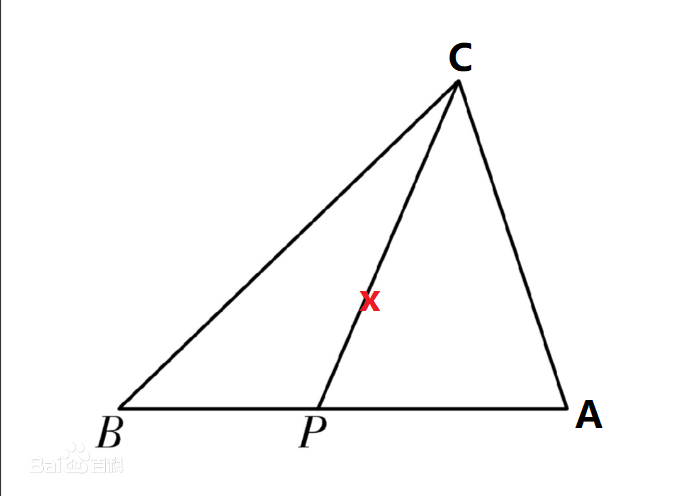
斯特瓦尔特定理
设已知△ABC及其底边上A、B两点间的一点P,则有
\[x^2=\frac{BC^2\cdot PA+AC^2\cdot BP}{AB}-PA\cdot PB
\]
证明
\(\cos\angle BPC+\cos\angle APC=0\)
然后整理一下就得到了结论
角平分线
补充这个条件
\[\frac{\sin\ang BCP}{\sin \ang BPC}=\frac{PB}{BC}=\frac{PA}{AC}=\frac{\sin\ang PCA}{\sin \ang APC}
\]
然后拿它和前面的斯特瓦尔特定理得到的式子联立,解出
\[x=\sqrt{ab[1-(\frac{c}{a+b})^2]}=\frac{2ab}{a+b}\cdot\cos(\frac{C}{2})
\]
中线
补充这个条件
\[PB=PA
\]
然后拿它和前面的斯特瓦尔特定理得到的式子联立,解出
\[x=\frac{1}{2}\sqrt{2a^2+2b^2-c^2}
\]
垂线
利用求三角形面积用到的海伦公式
\[x=\frac{2S}{c}
\]
其中\(S\)是三角形面积,\(S=\sqrt{p(p-a)(p-b)(p-c)},\text{where}\ p=\frac{a+b+c}{2}\)



