【备忘录】麦克斯韦速率分布

放弃改正错误，都去看这篇文章吧

 
 
 
 

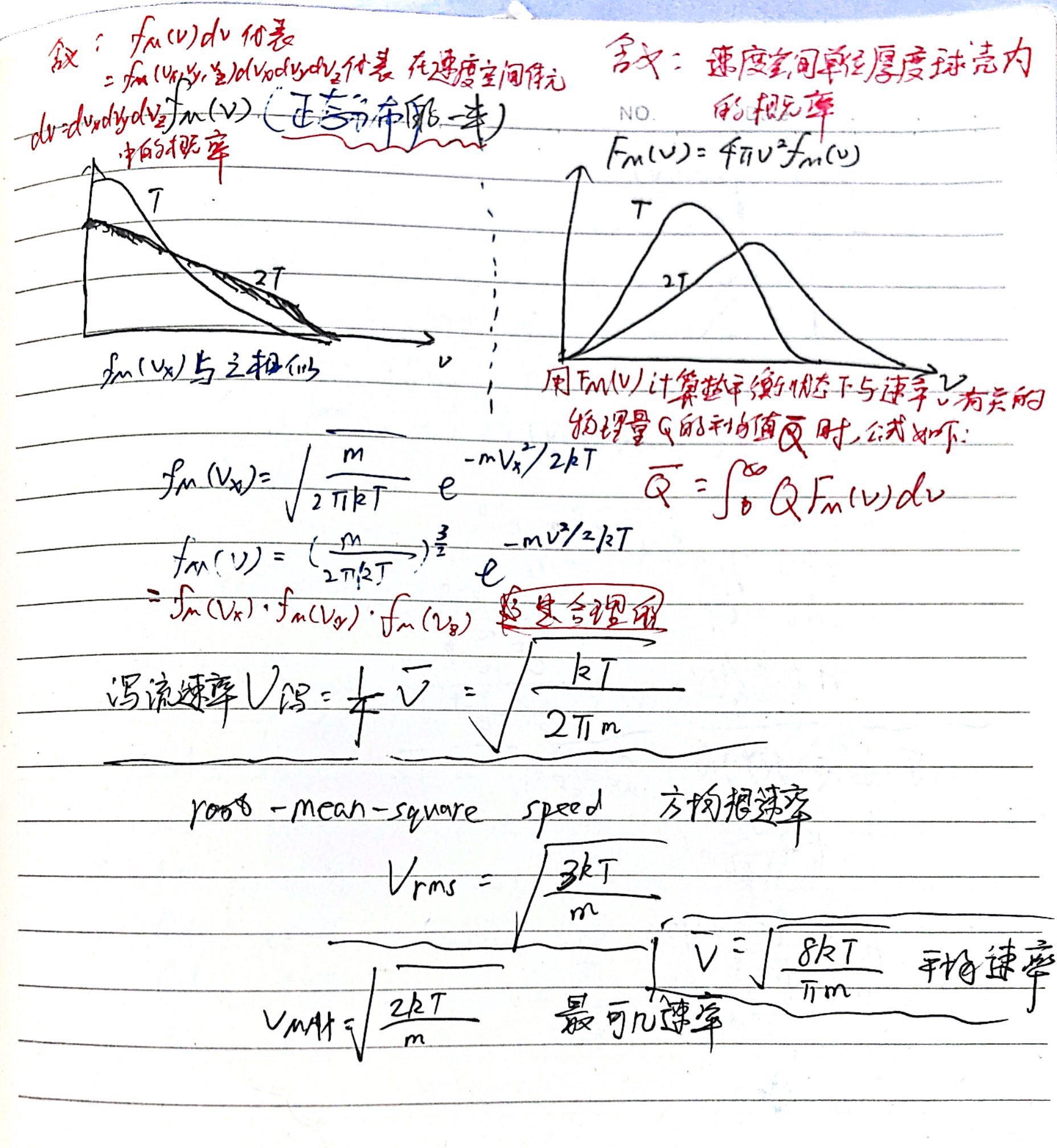
突然想做麦克斯韦速度分布的复习，找到了以前读《新概念物理学·热学》的笔记
发现高中时我如何臆测不得其解的东西竟然被这一页提纲挈领的笔记就解释很清楚了

如果让我给高中时的我带话帮助他迅速理解这东西的话，大概也就这些：(这里只讲我如何快速感性地理解这个东西，严谨的推导可以看《新概念物理学·热学》)
每个维度的分速度(矢量)$v_x,v_y,v_z$是服从正态分布的，而且相互独立
考虑速度空间，$v$处的概率体元是$f_M(v)\mathrm{d}v=f(v_x)\mathrm{d}v_xf(v_y)\mathrm{d}v_yf(v_z)\mathrm{d}v_z$,又因为$\mathrm{d}v=\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z$
$v$处的概率密度$f_M(v)=f(v_x)f(v_y)f(v_z)$
因为你要求的是速率分布，速度空间v处\mathrm{d}v厚度的球壳内的概率是$4\pi v^2f_M(v))\mathrm{d}v$

使用$\bar{Q}=\int_0^\infty Q F_M(v)\mathrm{d}v$计算出分子的平均动能是$\frac{3}{2}kT$,
以后还会知道能量均分定理，每个自由度的运动没有什么特殊性，都分到$\frac{1}{2}kT$
 
upd 2020-10-01 突然想起来悲伤的事：上次读《新概念物理学·热学》都是2018年10月了，这都是2018年10月份做的笔记了，现在不可能做成这样了

Clear["Global`*"];
$Assumptions = {m > 0, k > 0, T > 0};
fMvx[vx_] := Sqrt[m/(2*Pi*k*T)]*Exp[-m*vx^2/(2*k*T)];
Integrate[fMvx[vx], {vx, -Infinity, Infinity}]
fMv[v_] := (m/(2*Pi*k*T))^(3/2)*Exp[-m*v^2/(2*k*T)];
Integrate[4*Pi*v^2*fMv[v], {v, 0, Infinity}]
kineticEnergyAvg = 
  Integrate[1/2*m*v^2*(4*Pi*v^2*fMv[v]), {v, 0, Infinity}];
Print["kineticEnergyAvg=", kineticEnergyAvg];
amplitutevAvg = 
  Integrate[v*(4*Pi*v^2*fMv[v]), {v, 0, Infinity}] // FullSimplify;
Print["amplitutevAvg=", amplitutevAvg];
vMaximumLikelihood = 
  v /. Part[Solve[{D[4*Pi*v^2*fMv[v], v] == 0, v > 0}, v], 1];
Print["vMaximumLikelihood=", vMaximumLikelihood];