【读书笔记】组合计数-Tilings-正文 学一半的笔记
Tilings-正文部分
后面真就大段文字。。。
9.2 转移函数方法
例子
考察最简单的那个\(1\times 2\)多米诺填充 \(2\times n\)的例子，
看每一列，要么是一个vertical的\(1\times 2\)（记作V）,要么是两个horizonal的\(2\times 1\)的左半部分（记作L），要么是两个horizonal的\(2\times 1\)的右半部分（记作R）
你有6个阶段决策要做，限制是：
如果上一阶段是V,这一阶段可以V,L,R
如果上一阶段是L,这一阶段可以R
如果上一阶段是R,这一阶段可以V,L,R
建图的话就是这样：
节点的含义是，上面表示【不突出，不突出】，下面表示【突出，突出】
你结合着这道题理解一下就清楚了，但是两个建的不是一个图（我承认很像，拍扁后几乎一样，但是并不是一个图）
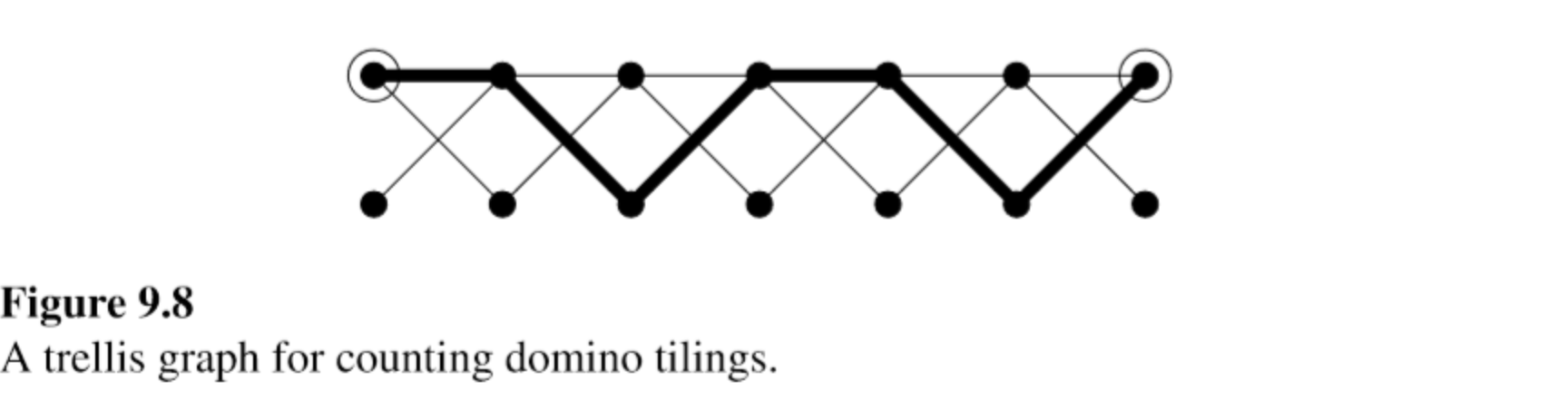
拿矩阵语言描述这个图就是
补充
- 它还说同样的处理方法可以运用到\(1\times 2\)多米诺填充 \(m\times n\)上去，这当然。复杂度一般来说\(O(n2^m)\)或者\(O(m2^n)\)
- 这种方法还能被运用到 tiling problems in which the region being tiled is “essentially one-dimensional” in the sense that only one dimension is growing as n increases.比如，\(1\times 1\times 2\) bricks填充 \(8\times 8\times n\) box.一般性的理论告诉我们\(a_n\)满足线性递归，然而，the span of this recurrence could be extremely long.
- 如果把\(\left(\begin{array}{ll} 1 & 1 \\ 1 & 0 \end{array}\right)\)换成\(M=\left(\begin{array}{ll} y & x \\ x & 0 \end{array}\right)\),得到的就不是数\(a_n\)而是x,y多项式。y表征一个水平多米诺，x表征一个竖直多米诺。这样 The upper-left entry of M6 is $ x^6 +6x4y2 +5x2y4 +y^6$ .可以看到\(1\times 2\)多米诺填充 $2\times6 $，其中正好4个竖直多米诺和2个水平多米诺的方案数是6
- 建模为完美匹配，物理学中类似的叫dimer configuration。回到那个xy例子，我们还能拿统计力学来做。blabla
9.3 其余的方法
9.3.1 the path method
把tile decorate一下，和path建立bijection.比如
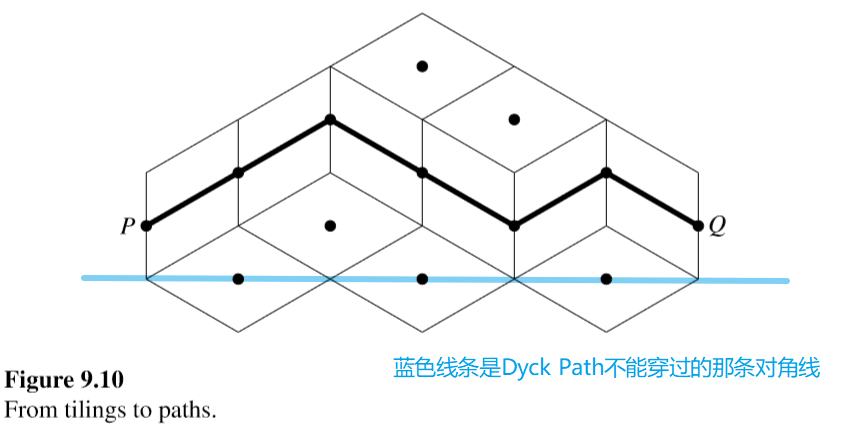
或者和routing建立bijection 举例
9.3.2 The permanent-determinant and Hafnian-Pfaffian method
没看
9.3.3 The spanning tree method
没看
9.4 表示理论方法
没看
9.5 其他的组合方法
Kuo condensation
9.6Related topics,and an attempt at history
联系物理，化学之类的
这里介绍前沿，大段文字。
9.7 Some emergent themes
9.7.1 Recurrence relations
这样的问题本质上还是求整数数列的问题。什么样的问题具有nice的answer?Niceness是主观的，我们这里说一个问题是nice的，如果序列被一些数学著作收录或者被OEIS收录或者有可被经验式地推导的特征(即，满足线性递归方程)。当\(a_n\)以指数级的\(n^2\)增长时，没有机会找到线性递归。我们还能做什么呢？
一个回答是有理递归。
blabla
9.7.2 Smoothness
一个序列称作smooth的，如果\(a_n\)的最大素因子是\(O(n)\)量级的；称作ultra smooth 的，如果\(a_n\)最大素因子是\(O(1)\)量级
Call a sequence a1,a2,..., smooth if the largest prime factor of \(a_n\) is O(n),
and ultra-smooth if the largest prime factor of an is O(1), that is, bounded. (Another word that is sometimes used instead of “smooth” is “round.”)
For example,
\(H(3n)H(n)^3/H(2n)^3\) (the number of lozenge tilings of a regular hexagon of side n) is smooth;
\(2^{n(n+1)/2}\) (the number of domino tilings of an Aztec diamond of order n) is ultra-smooth
经常的情况是我们计数问题的答案是smooth序列，smoothness经常是找到精确product formula的关键
9.7.3 Non-periodic weights
9.7.4 Other numerical patterns
9.7.5 Symmetry
9.8 Software
9.9 前沿Frontiers
书用的是Handbook of Enumerative Combinatorics by Miklos Bona
资料来自网络
