Probability Mass Function 离散随机变量的分布函数PMF
note 前半部分是Analytic Combinatorics by Philippe Flajolet, Robert Sedgewick的
III.2. Bivariate generating functions and probability distributions 这一节的笔记
note 2020-09-17 19:12 增加了《具体数学》里的PGF部分
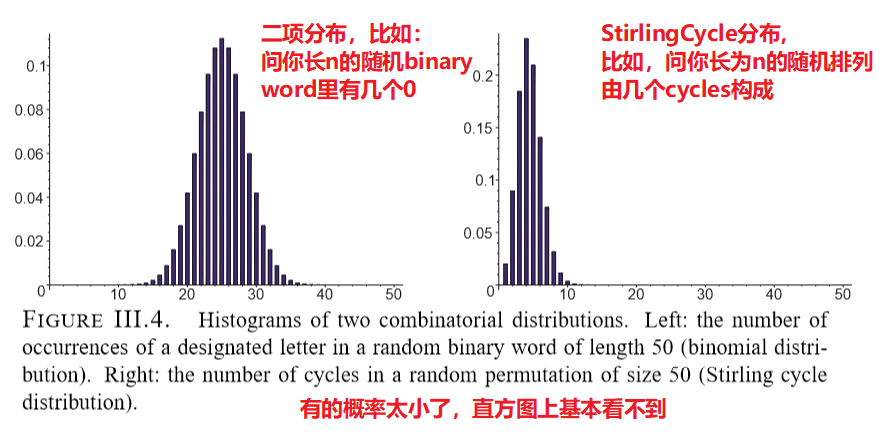
随机结构举例 two classical combinatorial distributions
PGF Probability generating functions定义
\[p(u)=\sum_{k} \mathbb{P}(X=k) u^{k}
\]
当然，能从BGF推到PGF
矩 Moments
The (power) moments are （r阶矩定义）
\[\mathbb{E}\left(X^{r}\right):=\sum_{k} \mathbb{P}\{X=k\} \cdot k^{r}
\]
The factorial moment defined for order r as (r order-阶乘矩定义)
\[E[X(X-1) \cdots(X-r+1)]
\]
从BGFs 推到 Moments
例题
二项分布的r order-阶乘矩
\[f_{n,k}=\binom{n}{k}
\]
先算出OBGF
\[W(z,u)=\frac{1}{1-z-zu}
\]
算出对\(u\)的\(r\)阶偏导,再取\(u=1\)
\[\left.\frac{\partial^{r}}{\partial u^{r}} W(z, u)\right|_{u=1}=\frac{r ! z^{r}}{(1-2 z)^{r+1}}=\frac{r ! (2z)^{r}}{2^r(1-2 z)^{r+1}}
\]
对\([z^n]\)反演得到【以\(n\)为变量，\(r\)为参数的某表达式】 (分子)
\[\left.\left[z^{n}\right] \partial_{u}^{r} W(z, u)\right|_{u=1}=\frac{r!}{2^r}\binom{n}{r}2^n
\]
\(W(z,1)\)对\([z^n]\)反演得到 (分母)
\[\left[z^{n}\right] W(z, 1)=[z^n]\frac{1}{1-2z}=2^n
\]
分子分母代入这个公式，得到r order-阶乘矩
\[\mathbb{E}_{\mathcal{A}_{n}}(\chi(\chi-1) \cdots(\chi-r+1))=\frac{\left.\left[z^{n}\right] \partial_{u}^{r} A(z, u)\right|_{u=1}}{\left[z^{n}\right] A(z, 1)}=\frac{r!}{2^r}\binom{n}{r}
\]
接着没事可以算算期望，方差
期望（1 order-阶乘矩）
\[\mathbb{E}_{\mathcal{A}_{n}}(\chi)=\frac{n}{2}
\]
用公式\(\mathbb{E}_{\mathcal{A}_{n}}\left(\chi^{2}\right)=\frac{\left.\left[z^{n}\right] \partial_{u}^{2} A(z, u)\right|_{u=1}}{\left[z^{n}\right] A(z, 1)}+\frac{\left.\left[z^{n}\right] \partial_{u} A(z, u)\right|_{u=1}}{\left[z^{n}\right] A(z, 1)}\)得到二次矩
\[\mathbb{E}_{\mathcal{A}_{n}}(\chi^2)=\frac{n(n-1)}{4}+\frac{n}{2}=\frac{n(n+1)}{4}
\]
使用方差公式\(\mathbb{V}(X)=\mathbb{E}\left(X^{2}\right)-\mathbb{E}(X)^{2}\)得到方差
\[\mathbb{V}(\chi)=\frac{n(n+1)}{4}-\frac{n^2}{4}=\frac{n}{4}
\]
附录
下面的内容来自《具体数学》中概率生成函数小节
为什么要使用概率生成函数？\(G(z)=\sum \Pr(X=k)z^k\)
一大长处是可以简化均值和方差的计算。（嗯这两个公式挺好证的，把右边展开成和式）
\[Mean(X)=G'(1)\\
Var(X)=G''(1)+G'(1)-G'(1)^2\\
E[X^2]=G''(1)+G'(1)
\]
第二大长处是：在许多重要的情形，它们都是\(z\)的比较简单的函数
第三大长处是：概率生成函数的乘积对应于(相互独立的)随机变量之和
然后有意思的是引入了累积量，和多阶矩、r-order阶乘矩很是像，都是数字特征里更加“高次”的东西。
定义\(\kappa_i\)是累积量，由下面的公式给出。由此定义式可见看出，由于【对数变乘为加】以及【概率生成函数的乘积对应于随机变量之和】，所以：独立随机变量之和的所有累积量也可由原来的对应累积量相加得到。
\[\ln G(e^t)=\frac{\kappa_1}{1!}t+\frac{\kappa_2}{2!}t^2+\frac{\kappa_3}{3!}t^3+\frac{\kappa_4}{4!}t^4+\dots
\]
定义\(\alpha_m\)是阶乘矩\(\alpha_m=E[X(X-1) \cdots(X-m+1)]\)
定义\(\mu_m\)是\(m\)阶矩，\(\mu_m=E[X^m]\)
把PGF \(G(e^t)\)各种改写，比对系数，得到这三个“高次量”的相互转换
拿\(\kappa_i\)写\(G(e^t)\) (把累计量的定义式取指数)
\[G(e^t)=1+\frac{\frac{\kappa_1}{1!}t+\frac{\kappa_2}{2!}t^2+\dots}{1!}+\frac{(\frac{\kappa_1}{1!}t+\frac{\kappa_2}{2!}t^2+\dots)^2}{2!}+\dots
\]
拿\(\mu_m\)写
\[\begin{aligned}
G(e^t)=\sum\limits_{k\geq 0}\Pr(X=k)e^{kt}&=\sum\limits_{k,m\geq 0}\Pr(X=k)k^m\cdot\frac{t^m}{m!}\\
&=1+\frac{\mu_1}{1!}t+\frac{\mu_2}{2!}t^2+\frac{\mu_3}{3!}t^3+\dots
\end{aligned}
\]
拿\(\alpha_m\)写
因为
\[\begin{aligned}
G(1+t)&=G(1)+\frac{G'(1)}{1!}t+\frac{G''(1)}{2!}t^2+\cdots\\
&=1+\frac{\alpha_1}{1!}t+\frac{\alpha_2}{2!}t^2+\cdots
\end{aligned}
\]
于是
\[\begin{aligned}
G(e^t)&=1+\frac{\alpha_1}{1!}(e^t-1)+\frac{\alpha_2}{2!}(e^t-1)^2+\cdots\\
&=1+\frac{\alpha_1}{1!}(t+\frac{t^2}{2}+...)+\frac{\alpha_2}{2!}(t^2+t^3+...)+\cdots
\end{aligned}
\]
