BGF bivariate generating function 双变量生成函数
目录
定义
BGF bivariate generating function
形式变量\(z\)对应于下标\(n\),形式变量\(u\)对应于下标\(k\)
BGF就是个二重求和

horizonal GF 和 vertical GF

例子
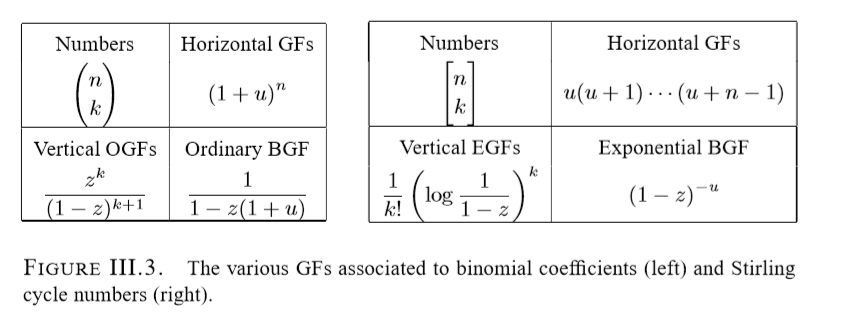
组合数
horizonal GF
\[W_{n}(u):=\sum_{k=0}^{n}\left(\begin{array}{l}
n \\
k
\end{array}\right) u^{k}=(1+u)^{n}
\]
vertical GF (Ord case)
\[W^{\langle k\rangle}(z)=\sum_{n \geq 0}\left(\begin{array}{l}
n \\
k
\end{array}\right) z^{n}=\frac{z^{k}}{(1-z)^{k+1}}
\]
vertical GF (Exp case)
\[\sum_{n \geq 0}\left(\begin{array}{l}
n \\
k
\end{array}\right) \frac{z^{n}}{n!}=e^zz^k/k!
\]
OBGF
先算行再算列,
\[W(z, u)=\sum_{k, n \geq 0}\left(\begin{array}{l}
n \\
k
\end{array}\right) u^{k} z^{n}=\sum_{n \geq 0}(1+u)^{n} z^{n}=\frac{1}{1-z(1+u)}
\]
先算列再算行
\[W(z, u)=\sum_{k \geq 0} u^{k} \frac{z^{k}}{(1-z)^{k+1}}=\frac{1}{1-z} \frac{1}{1-u \frac{z}{1-z}}=\frac{1}{1-z(1+u)}
\]
EBGF
先算行再算列
\[\widetilde{W}(z, u)=\sum_{k, n}\left(\begin{array}{l}
n \\
k
\end{array}\right) u^{k} \frac{z^{n}}{n !}=\sum(1+u)^{n} \frac{z^{n}}{n !}=e^{z(1+u)}
\]
第一类斯特林数
vertical GF (Exp case)
\[P^{\langle k\rangle}(z):=\sum_{n}\left[\begin{array}{l}
n \\
k
\end{array}\right] \frac{z^{n}}{n !}=\frac{1}{k !}(\mathbb{log}\frac{1}{1-z})^k
\]
EBGF
先算列再算行
\[\begin{aligned}
P(z, u) &:=\sum_{k} P^{\langle k\rangle}(z) u^{k}=\sum_{k} \frac{u^{k}}{k !} L(z)^{k}=e^{u L(z)} \\
&=(1-z)^{-u}
\end{aligned}\\
where\ L(z)=\mathbb{log}\frac{1}{1-z}
\]
间接求horizonal GF
\[\mathbb{expand} \ \ P(z,u)=(1-z)^{-u},\\
P(z,u)=(1-z)^{-u}=\sum_{n \geq 0}\left(\begin{array}{c}
n+u-1 \\
n
\end{array}\right) z^{n}
\]
\[\mathbb{horizonal} \ GF \ \ \ \ P_n(u)=u(u+1)(u+2)...(u+n-1)
\]