University of Toronto Faculty of Arts and Science MAT344– Final Assessment Combinatorics Instructors: Stanislav Balchev and Max Klambauer 19 August 2020

目录

• T1
• T2
• T3
• T4
• T5
  • solution to (a)
  • solution to (b)
  • solution to (c)
  • solution to (d)
• T6
• T7
• T8
• T9

总共9题，这里选择性地做一下。

时间仓促，没有核对答案。

T1

Give a formula for the number of lattice paths from (0,0) to (3n,n) where there are no instances of a vertical step being followed by another vertical step.

dp呗

\(dp[i][j][0]\)表示是1个horizonal step来到(i,j)的方法数

\(dp[i][j][1]\)表示是1个vertical step来到(i,j)的方法数

\[dp[i][j][0]=dp[i-1][j][0]+dp[i-1][j][1]\\ dp[i][j][1]=dp[i][j-1][0]\\ ans[i][j]=dp[i][j][0]+dp[i][j][1] \]

边界条件

\[dp[i][0][0]=1 \\ dp[i][0][1]=0 \\ for \ i\geq1 \\ dp[0][1][0]=0 \\ dp[0][1][1]=1 \\ \\and\\ dp[0][j][0]=0 \\ dp[0][j][1]=0 \\ for \ j\geq1 \]

嗯这个肯定有简单的方法，但我暂时没想到

T2

给你一个图，问你它是不是平面图或者是不是和平面图同构？给出理由

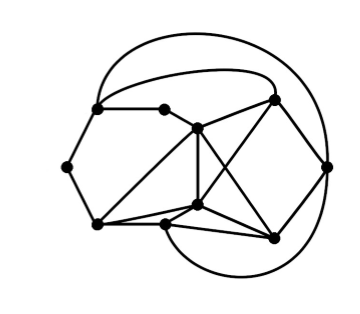
直接上库拉托夫斯基定理Kuratowski's Theorem

一个图是平面的当且仅当它不包含同胚于\(K_5\)或\(K_{3,3}\)的子图
A graph is planar if and only if it contains no subdivision of either \(K_5\) or \(K_{3,3}\)

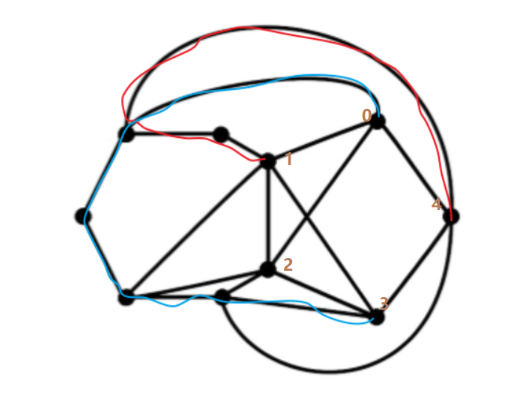
我找了半天，你可以看到一个同胚于\(K_5\)的子图，所以图\(G\)不是平面图

用那个Euler不等式

\(e>3v-6\),则图\(G\)非平面图

\(19<24\) 没作用

T3

图形的色数是产生图形正确着色所需的最小颜色数。(点染色)

首先团数clique number(能找到的最大\(i\),存在子图是完全图\(K_i\))是3，那么色数至少是3

提示已经给到位了，我们把字符串看成十进制数，然后按照%3的余数进行染3种色：比如mod3为0染0号色；mod3为1染1号色；mod3为2染2号色

考虑颜色相同的两个不同的点，它们肯定不相邻，因为相邻的点mod3一定不等。

这说明我们找到了3种颜色点染色的方案。

所以，图\(G\)的色数是3

T4

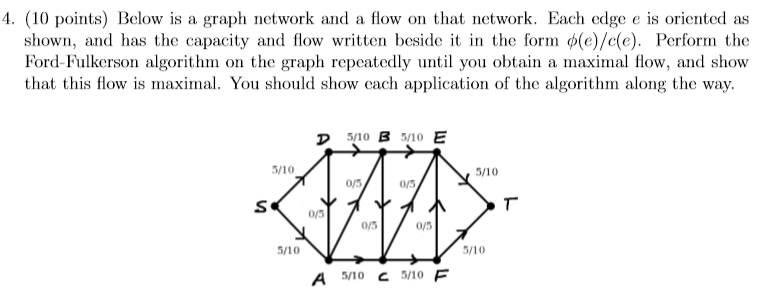
手解Ford-Fulkerson algorithm

算了这算法我没弄明白过

吐个槽，我差点和那个求最短路的Bellman Ford algorithm弄混了

但是这题给的例子太弱了，甚至可以直接看出来

可以先把比边权都除以5，方便计算

最后的最大流是20，一种方案是

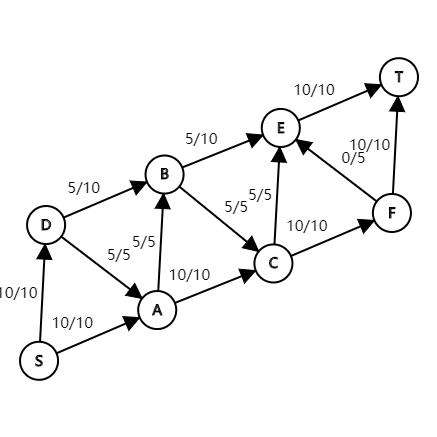
T5

solution to (a)

EGF板子题

\[\begin{aligned} (...+\frac{x^6}{6!}+\frac{x^4}{4!}+\frac{x^2}{2!}+1)^2\cdot(...+\frac{x^7}{7!}+\frac{x^5}{5!}+\frac{x^3}{3!}+x)^2\\ =(\frac{e^x+e^{-x}}{2})^2(\frac{e^x-e^{-x}}{2})^2\\ =\frac{e^{4 x}}{16}+\frac{1}{16} e^{-4 x}-\frac{1}{8} \end{aligned} \]

反演回去

\[a_n=\frac{1}{16}[4^n+(-4)^n]+\frac{-1}{8}[n==0] \]

solution to (b)

这时候就要用到博大精深的汉语了

12人5工程，每个工程至少1人，每人最多1工程。

\[12*11*10*9*8*6^{12-5} \]

solution to (c)

30个不同球放5个不同帽子。每个帽子至少1个球，但是1个帽子里不能装所有球。

水题。

$ 5!\cdot S_2(30,5)-5$

\(S_2(n,m)\)是第二类斯特林数，把\([n]\)分为\(m\)个非空子集的划分个数

solution to (d)

n=15的错排是吗？没理解错的话

https://oeis.org/A000166

人生苦短，记不住显式的公式\(f(n)=n!(\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-...(-1)^n\frac{1}{n!})\)还是递推吧

\[f(1)=0,f(2)=1,f(3)=2,f(4)=9,f(5)=44 \]

\[f(n) = (n-1)[f(n-2)+f(n-1)] (n>2) \]

递推式的证明：

考虑排列的圆分解，错排(derangement）是说长度为1的cycle的个数为0。

考虑最后一个元素\(n\)，如果它所在的cycle长度\(\geq 3\)，这相当于把\(n\)插入到(n-1)-错排排列的圆分解的\((n-1)\)个间隙之一，这有\((n-1)f(n-1)\)种，贡献了第一项

如果它所在的cycle长度为2，相当于从[n-1]中选出一个与\(n\)构成【互相置换】，剩下的n-2个构成错排，这有\((n-1)f(n-2)\)种，贡献了第二项

T6

T7

\[(1+x)(1+x^2+x^4)(1+x^3+x^9)(1+x^4+x^8+x^{12}+x^{16})... \]

T8

没看懂

T9

先做EGF

\[f''-3f'-10f=25xe^{5x} \]

\[f=c_1 e^{-2 x}+c_2 e^{5 x}+\frac{25}{686} e^{5 x} \left(49 x^2-14 x+2\right) \]

再反演回去

\[c_1(-2)^n+c_2(5)^n+\frac{25}{686}a_n \]

其中

\[a_n= \left\{ \begin{array}{**lr**} 2, \ \ for\ n=0 \\ -4 ,\ \ for \ n=1 \\ 5^{n-2}[49n(n-1)-70n+50] ,\ for\ n\geq 2 \end{array} \right. \]