【读书笔记】排列研究-模式避免-基础Pattern Avoidance

放弃更新，去看这个The Permutation Pattern Avoidance Library

但是这个网站懒得去给你做名词解释，你可能和我一样刚进去不知道啥是Proof Tree和System of Equations

你应该看这篇2022年8月放在arXiv上的99页的论文 https://arxiv.org/pdf/2202.07715.pdf

先讲了啥是Sums and Skew Sums of Permutations

然后讲了132-avoiding permutations class的graphical depiction。这个图说的就是：找到最大值所在的位置，【该位置左侧的任意元素】比【该位置右侧的任意元素】都要大。
这样就能avoid pattern 132.

接着了解一下Proof Tree和System of Equations的对应关系。

目录

• 模式避免的定义
• 避免Pattern q 的n-排列计数\(S_n(q)\)
  • q长度是2
  • q长度是3
  • 对一些模式q,做\(S_n(q)\)的阶估计
  • Backelin, West, and Xin给出的较为一般的Theorem
  • q长度是4
• 证明Stanley-Wilf conjecture
  • The Stanley-Wilf conjecture
  • The Füredi-Hajnal conjecture

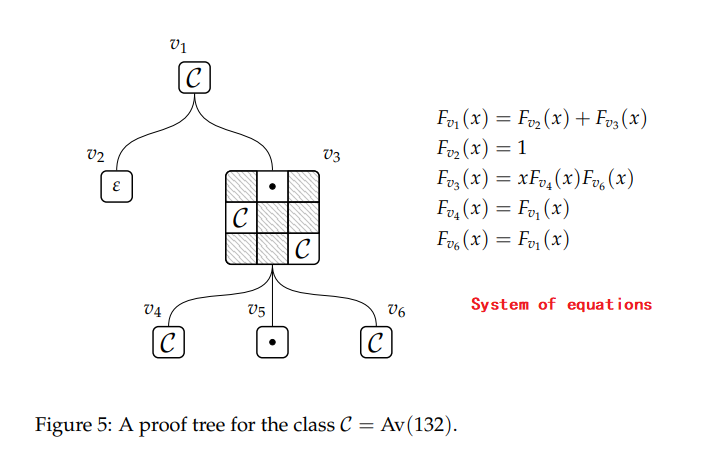
模式避免的定义

避免Pattern q 的n-排列计数\(S_n(q)\)

先扔结论，有时间把证明粘过来

q长度是2

\[S_n(12)=S_n(21)=1 \]

q长度是3

All patterns of length three are avoided by the same number of n-permutations.

\[S_n(123)=S_n(132)=S_n(213)=S_n(231)=S_n(312)=S_n(321)\\ S_{n}(132)=C_{n}=\frac{\left(\begin{array}{c} 2 n \\ n \end{array}\right)}{n+1} \]

对一些模式q,做\(S_n(q)\)的阶估计

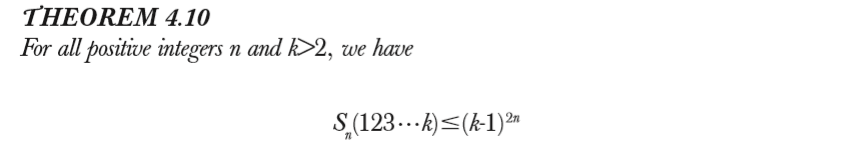
Backelin, West, and Xin给出的较为一般的Theorem

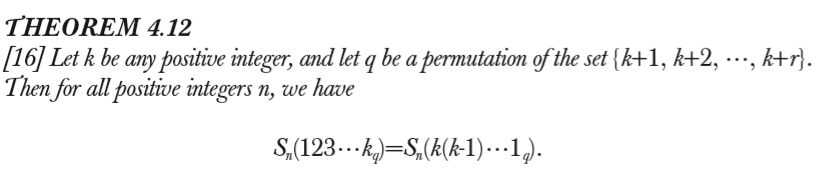
举例，
\(r=2,k=2,q=34\) it says, \(S_n(1234)=S_n(2134)\)
\(r=2,k=2,q=43\) it says, \(S_n(1243)=S_n(2143)\)
\(r=3,k=1,q=4\) it says, \(S_n(1234)=S_n(3214)\)

q长度是4

本来\(q\)有24种，可以证明最后归结为这三种代表,1234,1342,1324

\[\begin{aligned} &\text { for } S_{n}(1342) \text { we have } 1,2,6,23,103,512,2740,15485\\ &\text { for } S_{n}(1234) \text { we have } 1,2,6,23,103,513,2761,15767\\ &\text { for } S_{n}(1324) \text { we have } 1,2,6,23,103,513,2762,15793 \end{aligned} \]

aovid 1342 A022558

avoid 1234 A005802

avoid 1324 A061552

\[\begin{aligned} S_{n}(1342) &=(-1)^{n-1} \cdot \frac{\left(7 n^{2}-3 n-2\right)}{2} \\ &+3 \sum_{i=2}^{n}(-1)^{n-i} \cdot 2^{i+1} \cdot \frac{(2 i-4) !}{i !(i-2) !} \cdot\left(\begin{array}{c} n-i+2 \\ 2 \end{array}\right) \end{aligned} \]

\[S_{n}(1234)=2 \cdot \sum_{k=0}^{n}\left(\begin{array}{c} 2 k \\ k \end{array}\right)\left(\begin{array}{l} n \\ k \end{array}\right)^{2} \frac{3 k^{2}+2 k+1-n-2 n k}{(k+1)^{2}(k+2)(n-k+1)} \]

\[S_{n}(1234)=\frac{1}{(n+1)^{2}(n+2)} \sum_{k=0}^{n}\left(\begin{array}{c} 2 k \\ k \end{array}\right)\left(\begin{array}{c} n+1 \\ k+1 \end{array}\right)\left(\begin{array}{c} n+2 \\ k+1 \end{array}\right) \]

证明Stanley-Wilf conjecture

The Stanley-Wilf conjecture

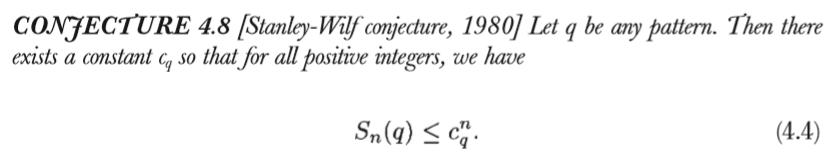
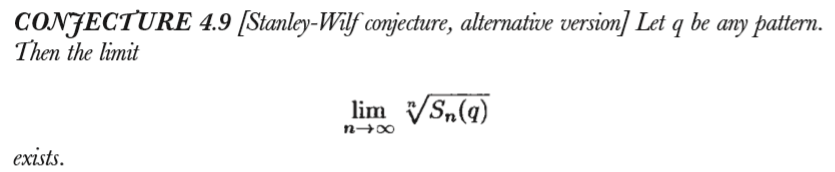
书里给出的思路是先丢个 The Füredi-Hajnal conjecture出来，说这个 The Füredi-Hajnal conjecture可以推导Stanley-Wilf conjecture.

这样我们先来研究The Füredi-Hajnal conjecture

The Füredi-Hajnal conjecture

\[f(n, P) \leq c_{p} n \]

先空着

资料来自网络

书用的是Combinatorics of permutations by Miklos Bona