使用Mathematica做序列的DTFT的几个例子

ListFourierSequenceTransform[{-2, -1, 1, 3, 3, 1, -1, -2}, \[Omega]]
ParametricPlot[{Re[%], Im[%]}, {\[Omega], -2 Pi, 2 Pi}, AspectRatio -> 1]
Plot[Abs[%%], {\[Omega], -2 Pi, 2 Pi}]
Plot[Arg[%%%], {\[Omega], -2 Pi, 2 Pi}]

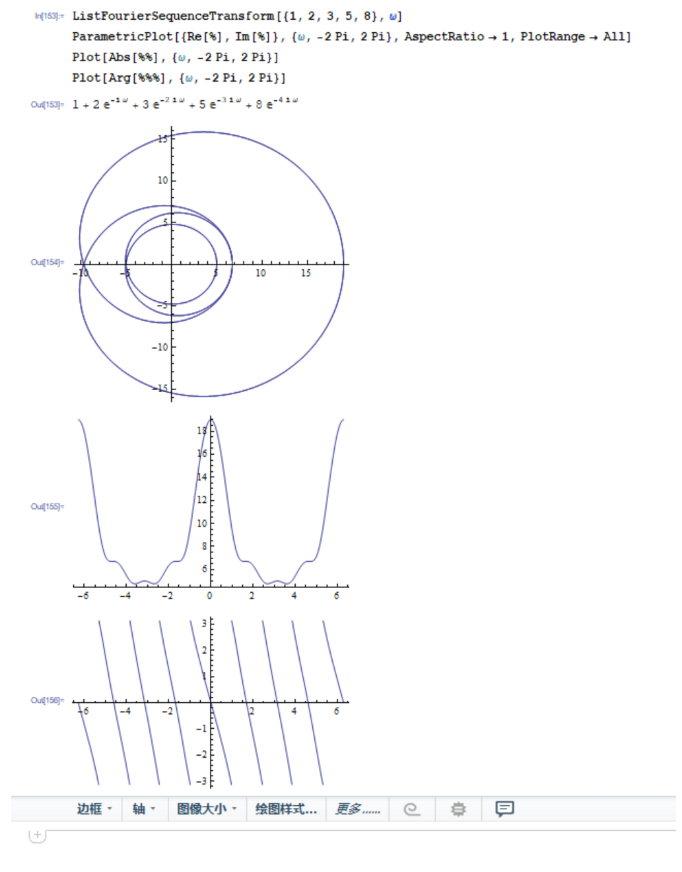
整活没活整了，将就着看吧，这程序也好写。
不查文档自己写的话也行，但是可能写得长一点。

---

upd 2021-01-23

试题求求你不要问我一个序列的性质如何，然后DTFT的性质如何了
blahblah一大堆，多举几个满足题意的例子就行了。

送个分析实部和虚部的孪生版本

ListFourierSequenceTransform[{-2, -1, 1, 3, 3, 1, -1, -2}, \[Omega]]
ParametricPlot[{Re[%], Im[%]}, {\[Omega], -2 Pi, 2 Pi}, AspectRatio -> 1]
Plot[Re[%%], {\[Omega], -2 Pi, 2 Pi}]
Plot[Im[%%%], {\[Omega], -2 Pi, 2 Pi}]

下面这个懂我意思吧，比如你的序列不是从下标0开始就这么写。无限长或半无限长的序列做DTFT还是Sum[]吧。
下标从-3开始

ListFourierSequenceTransform[{1, 2, 3, 4, 5}, \[Omega], -3]

下标从3开始

ListFourierSequenceTransform[{1, 2, 3, 4, 5}, \[Omega], 3]

---

upd 2021-12-5 实用代码整理

更新一些代码
DFT.m
拿MATLAB算DFT

clear all;
close all;
clc;

N=64;
q=2.5;
n=[0:1:N-1];
x=cos(2*pi*n*q/N);
X=fft(x,N);
% X
subplot(2,1,1);
stem(abs(X));
title('the amplitude of DFT');
subplot(2,1,2);
stem(angle(X));
title('the angle of DFT');
yticks([-pi,-pi/2,pi/2,pi]);

DFT.nb
拿Mathematica算DFT

NN = 64; q = 2.5;
list = Table[Cos[2*Pi*n*q/NN], {n, 0, NN - 1}];
ans = Fourier[list];
ListPlot[Abs[%], PlotRange -> All]
ListPlot[Arg[%%], PlotRange -> All]

CTFT.nb
拿Mathematica算连续时间傅里叶变换

FourierTransform[Cos[Pi*t], t, \[Omega], 
  FourierParameters -> {1, -1}] // FullSimplify
InverseFourierTransform[%, \[Omega], t, 
  FourierParameters -> {1, -1}] // FullSimplify


FourierTransform[Sign[1 - t] + Sign[1 + t], t, \[CapitalOmega], 
  FourierParameters -> {1, -1}] // FullSimplify
InverseFourierTransform[%, \[CapitalOmega], t, 
  FourierParameters -> {1, -1}] // FullSimplify

DTFT.nb
拿Mathematica算DTFT

ListFourierSequenceTransform[{-2, -1, 1, 3, 3, 1, -1, -2}, \[Omega],-3](*下标从-3开始*)
ParametricPlot[{Re[%], Im[%]}, {\[Omega], -2 Pi, 2 Pi}, AspectRatio -> 1]
Plot[Re[%%], {\[Omega], -2 Pi, 2 Pi}]
Plot[Im[%%%], {\[Omega], -2 Pi, 2 Pi}]