【读书笔记】排列研究-置换角度(分解为Products Of Cycles) 含GroupExploer使用

upd 2020-08-06 23:11完成了最初稿

目录

• 定义
• 开胃菜 entrée
• 群论角度
• 应用：几何变换
• 当然要从第一类斯特林数的角度来考虑一下
  • 一个排列的type定义
  • 排旗公式
  • 应用-共轭排列
  • 应用-树和Transposition换位
    • 定义
    • 结论
  • 回到正题——讲(无符号)第一类斯特林数

开篇警告❗全是群论
开篇警告❗全是群论
开篇警告❗全是群论
开篇警告❗全是群论
开篇警告❗全是群论
开篇警告❗全是群论
开篇警告❗全是群论

定义

一个排列的cycle decomposition:如标题所示，不解释。这里把一个排列看成一个置换\(f\)了。记号上就是：举例，置换215463的圆分解(1 2)(3 5 6)(4)

已知\(f\)的结构，\(f^m\)是Identity，让你求\(m\)。\(m\)称作\(f\)的阶(order)。\(m\)是\(\operatorname{lcm}\)(f的各个cycle长度）

定义permutation matrices 下面两种定义互为转置矩阵,而且\(A_pB_p=B_pA_p=I\)

\[举例\\ If \ p=2413=(4312), then\ we\ have\ \\ A_{p}=\left(\begin{array}{llll} 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{array}\right) \\ B_{p}=\left(\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right) \]

自然而然的会问二者中哪一种定义更好用？

考虑到\(B_{pq}=B_q\cdot B_p\)和\(A_{pq}=A_p\cdot A_q\) (\(A_{pq}\)记号的意思是【先p置换再q置换成新的置换】的矩阵）\(A_p\)的定义可能更合适。

比如要把一个列向量\(x=(x_1,x_2,x_3,x_4)^T\)置换为\(x=(x_2,x_4,x_1,x_3)^T\) 矩阵记号就是\(B_px\)    \(B_q(B_px)=B_{pq}(x)\)

如果是行向量\(y\)的话，矩阵记号就是\(yA_p\)    \(yA_{pq}=yA_pA_q\)

开胃菜 entrée

定义一个排列是奇/偶的，如果逆序对个数是奇/偶的

A permutation that consists of exactly one even cycle is odd.

A permutation that consists of exactly one odd cycle is even.

群论角度

写到这里我要恶补一下 《群论——可视化方法》的 5.4对称群和交错群

接着看别人制作的出色群论科普项目Group Exporer

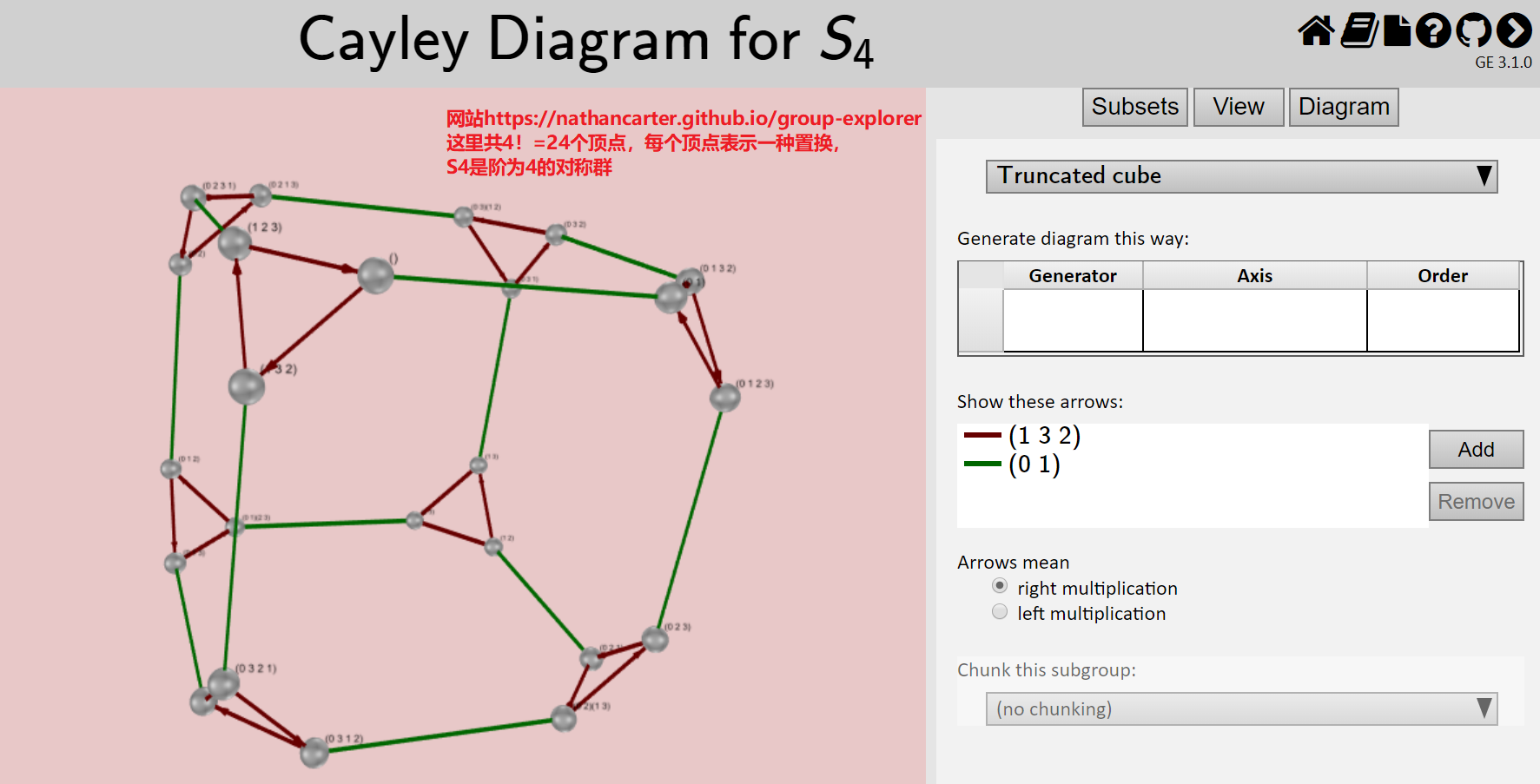
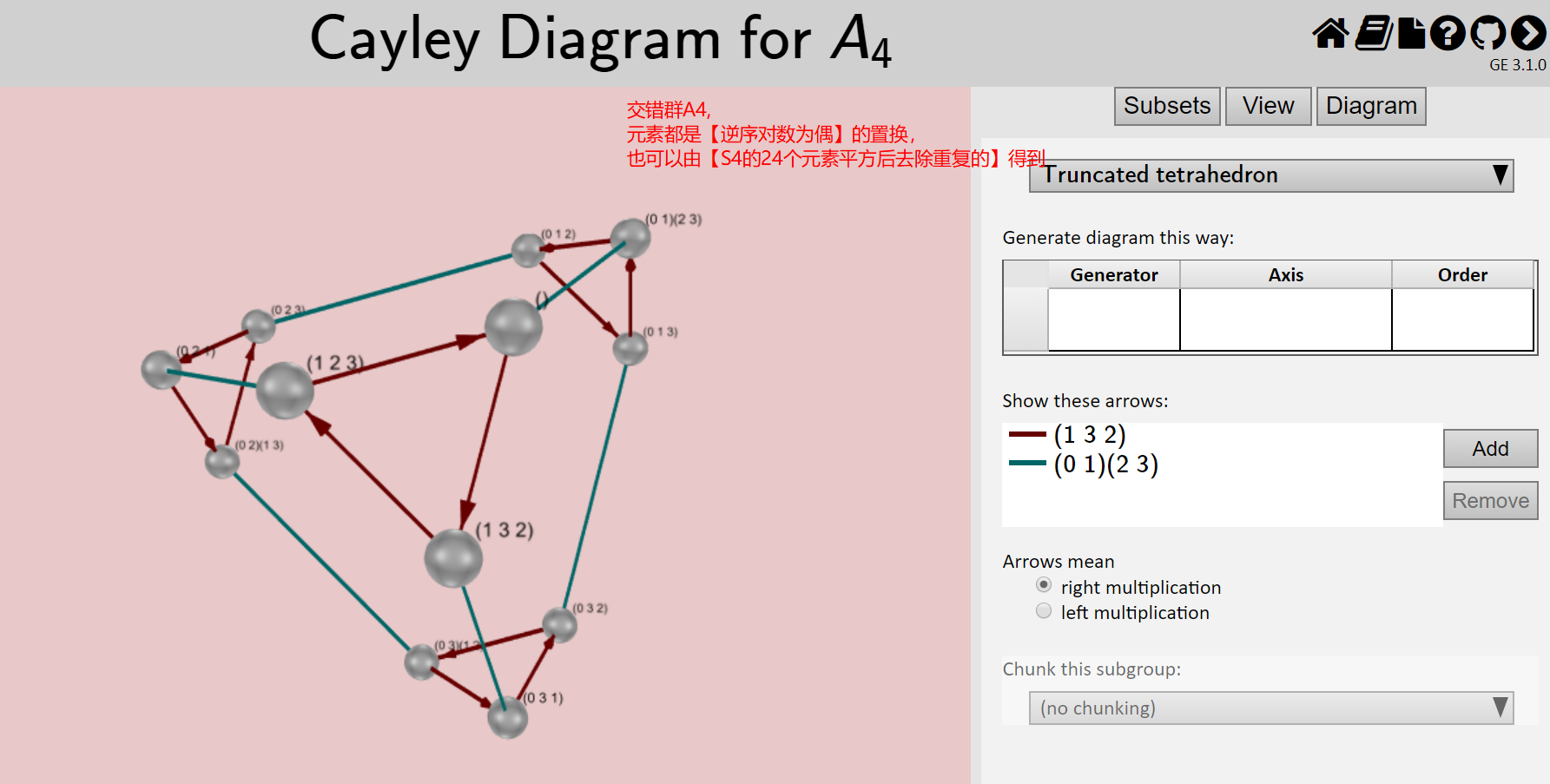
应用：几何变换

先介绍两面正多边形纸片和对应的\(D_n\)二面体群。然后好像是点标号，把旋转和翻转理解为置换

接着提了一下三维的正方体在三维空间中的刚体运动（那么只考虑绕轴旋转），正方体的旋转群是\(S_4\)

关于离散子群的一些杂记@陆zz

当然要从第一类斯特林数的角度来考虑一下

把\(n\)人分成\(k\)个圆桌排列。。。

一个排列的type定义

先定义一个排列的type：排列圆分解后，有\(a_i\)个长度为\(i\)的cycles，\((a_1,a_2,...,a_n)\)就称作排列的type

举例：The permutation p=(21) (534) (6) (987) is of type (1, 1, 2, 0, 0, 0, 0, 0, 0).

从排列的type定义就可以看出来，按照type的不同把置换分成了\(p(n)\)个等价类，有\(p(n)\)个type         (\(p(n)\)是分拆数)

排旗公式

\(\mathrm{PROPOSITION 3.12}\)

Let \(\left(a_{1}, a_{2}, \cdots, a_{n}\right)\) be an n-tuple of nonnegative integers so that \(\sum_{i=1}^{n} a_{i} \cdot i=n\) ,Then the number of n-permutations of type \(\left(a_{1}, a_{2}, \cdots, a_{n}\right)\) is

\[\frac{n !}{a_{1} ! a_{2} ! \cdots a_{n} ! 1^{a_{1}} 2^{a_{2}} \ldots n^{a_{n}}} \]

没得讲，高中时的排旗公式(给你红白蓝的棋子各若干，问你能组成多少种旗语;计算三国杀1主公1内奸2忠臣4反贼可能坐位,如果反贼间无区别，忠臣间无区别，主公总在一号位)

应用-共轭排列

In the symmetric group \(S_n\), two permutations \(g\) and \(h\) are called conjugates of each other if there exists an element \(f\in S_n\)so that \(ƒgƒ^{-1}=h\) holds. (有点像线性代数里的矩阵相似)

对称群\(S_n\)中的置换\(g\)和\(h\)共轭，当且仅当\(g\)和\(h\)是相同的type

we showed that conjugating by \(f\) turned the cycle \(\left(b_{1} b_{2} \cdots b_{k}\right)\) into the cycle \(\left(f^{-1}\left(b_{1}\right) f^{-1}\left(b_{2}\right) \cdots f^{-1}\left(b_{k}\right)\right) .\)

应用-树和Transposition换位

定义

换位，两个不同位置的元素交换，(i,j) transposition

相邻换位，两个相邻位置的元素交换，(i,i+1) adjacent transposition

一个排列是cyclic的，当且仅当排列的圆分解就是一个圆 比如4123

结论

Prove that any element of \(S_n\) can be obtained as a product of (not necessarily distinct) adjacent transpositions. 不解释

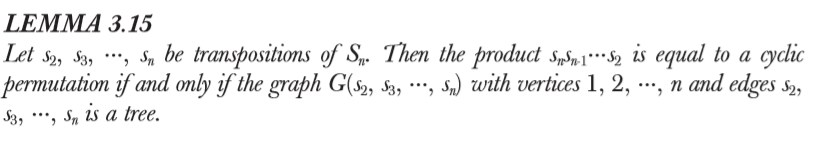
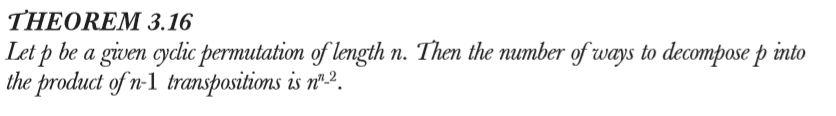
回到正题——讲(无符号)第一类斯特林数

先空着

资料来自网络

书用的是Combinatorics of permutations by Miklos Bona