数论函数相关的博客整理

数论函数相关的博客整理

http://blog.leanote.com/post/rockdu/TX20 理解快速沃尔什变换/快速莫比乌斯变换(FWT|FMT) (已完结)
https://blog.csdn.net/startaidou/article/details/90900258 莫比乌斯变换总结
https://blog.csdn.net/Ivanzn/article/details/88641049 数论函数（一）
https://blog.csdn.net/qq_35703773/article/details/85846839 常见数论函数总结
https://blog.csdn.net/henucm/article/details/96866245 二项式反演
https://wenku.baidu.com/view/9e1a5829647d27284b735195.html 清华《组合数学》反演理论
https://www.cnblogs.com/zhouzhendong/p/Number-theory-Function.html 数论函数 - 莫比乌斯函数与莫比乌斯反演 - 基础杜教筛

 
2020-11-05 突然发现个我曾经就意识到但是并不在意现在却真实影响到我的问题（我把它当成房间里的大象了？）：我只是复制粘贴自己收集到的链接贴到这里，我甚至都没有开始理解它，这算什么呢？
2021-02-12 我对数论一无所知。。。
2021-03-29 再扔几个链接
Chapter 1 Number-Theoretic Function
Integer Functions -- from Wolfram MathWorld
Number Theoretic Functions -- from Wolfram MathWorld
斯坦福的Number Theory - Number Theory
维基百科上关于数论函数的词条
 
 

 

目录

• Euler totient function
• 素因子个数
• 素因子的幂的和
• Carmichael function
• 莫比乌斯数论函数
• von Mangoldt function
• Prime counting function
• \(\sigma_k(n)\) 因子的k次方幂和
• \(r_k(n)\) Sum of k squares
• Dirichlet convolution

Euler totient function

小于n而且和n互质的数的个数

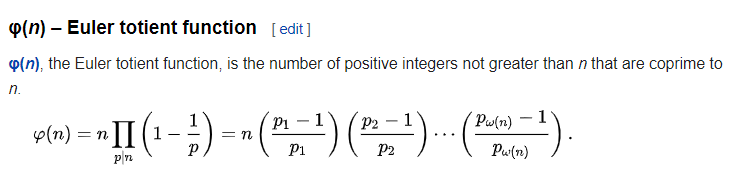
Table[EulerPhi[k], {k, 0, 20}]

print(vector(21, n,  eulerphi(n-1) ));

 
 
 
 
如果质因数分解\(n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}\)

素因子个数

\[\omega(n)=k \]

Table[PrimeNu[k],{k,10}]

print(vector(10, n,  omega(n) ));

素因子的幂的和

\[\Omega(n)=a_1+a_2+...+a_k \]

Table[PrimeOmega[k],{k,10}]

Carmichael function

mma里给出的译名是：卡迈克尔的\(\lambda\)函数
定义为使得对所有的与 n 互素的 k 都有 \(k^{m} \equiv 1 \bmod n\)的最小整数 m.

Table[CarmichaelLambda[k], {k, 10}]

莫比乌斯数论函数

当 n 为偶数个不同素数的乘积时，\(\mu(n)\) 为 1；当 n 为奇数个不同素数的乘积时 \(\mu(n)\) 为 -1；当 n 有多个素因子时，\(\mu(n)\) 为 0.

 

直接理解就是
如果 n可以写成\(p_1p_2...p_k\)的形式，那么：\(\mu(n)=(-1)^k\)
如果 n素因数分解后，某个素数的指数>=2了，那么\(\mu(n)=0\)
否则 \(\mu(n)=1\) （对应n=1的情形）

Table[MoebiusMu[k], {k, 10}]

{1, -1, -1, 0, -1, 1, -1, 0, 0, 1}

print(vector(10, n,  moebius(n) ));

规定\(\mu(1)=1\)
\(2=2\),所以\(\mu(2)=-1\)
\(3=3\)，所以\(\mu(3)=-1\)
\(4=2^2\)，所以\(\mu(4)=0\)
\(5=5\)，所以\(\mu(5)=-1\)
\(6=2*3\)，所以\(\mu(6)=1\)
\(7=7\)，所以\(\mu(7)=-1\)
\(8=2^3\)，所以\(\mu(8)=0\)
\(9=3^2\)，所以\(\mu(9)=0\)
\(10=2*5\)，所以\(\mu(10)=1\)

von Mangoldt function

Table[MangoldtLambda[k], {k, 10}]

Prime counting function

\[\pi(x)=\sum\limits_{p\leq x}1 \]

Table[PrimePi[k],{k,10}]

print(vector(10, n,  primepi(n) ));

\(\sigma_k(n)\) 因子的k次方幂和

DivisorSigma[2, 20](*20的因数的平方和*)

\(r_k(n)\) Sum of k squares

SquaresR[2, 45](*45可以表示成2个平方数的方案数目，8*)

Dirichlet convolution

\[(f*g)(n)=\sum\limits_{ab=n}f(a)g(b) \]

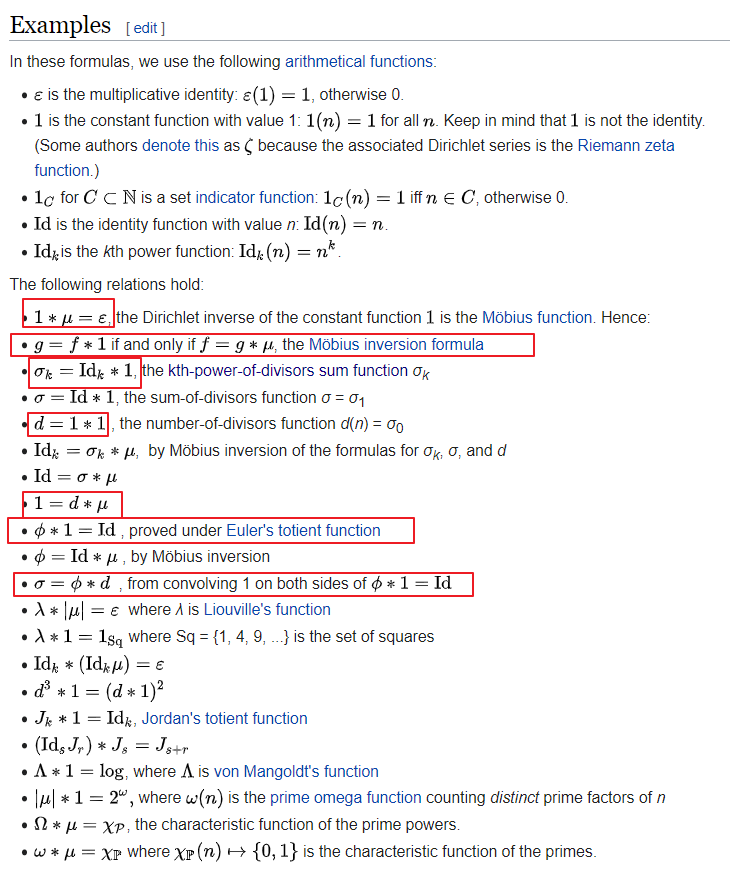
图片来自维基百科