【读书笔记】有序分拆和无序分拆的结论速览

目录

• • EXAMPLE I.4. Compositions with restricted summands
  • EXAMPLE I.5. Partitions with restricted summands (硬币找零问题）
  • EXAMPLE I.6. Compositions with a fixed number of parts.
  • EXAMPLE I.7. Partitions with a fixed number of parts
  • 结论表格
  • 最后还有一些
  • SEE ALSO
  • Basic Hypergeometric Series这本书的8.10节也给出了一些公式
• 分拆方案数里的一些等式

composition是带序的分拆（不允许和数有0）
partition 是不带序的分拆（不允许和数有0）
Cyclic compositions (wheels)是说有序分拆，然后做个圆排列
Partitions into distinct summands. 字面意思

主要的研究方法是：

由组合对象间的关系推出或者直接写出OGF

然后如果好反演的话找到通项公式\(a_n=[z^n]f(z)\)，不好反演就算了

接着通项简单的话直接分析渐进性质，否则用分析方法研究\(f(z)\)得到\(a_n\)的渐进性质

upd 2021-03-29 今天读了Stanley的《计数组合学·第一卷》第一章的开始的部分，里面提到了如何计数有如下的几种常见方法：
1.如果简单，直接写出显式公式
2.写出递推式和边界条件，也可以算是得到了可靠的结果
3.给出它关于变量的渐进估计
4.用生成函数描述

 

EXAMPLE I.4. Compositions with restricted summands

EXAMPLE I.5. Partitions with restricted summands (硬币找零问题）

(32)这里按我的想法解释的话，展开是\((1+x+x^2+...)(1+x^2+x^4+x^6+...)(1+x^3+x^6+x^9+...)...(1+x^r+x^{2r}+x^{3r}+...)\)
你第一个括号里拿的是\(x^4\),说明你的分拆里有4个1;...;你最后一个括号里拿的是\(x^{2r}\),说明你的分拆里有2个r

EXAMPLE I.6. Compositions with a fixed number of parts.

EXAMPLE I.7. Partitions with a fixed number of parts

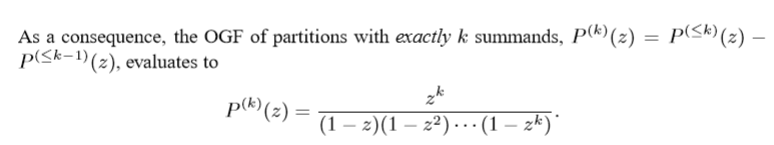
结论表格

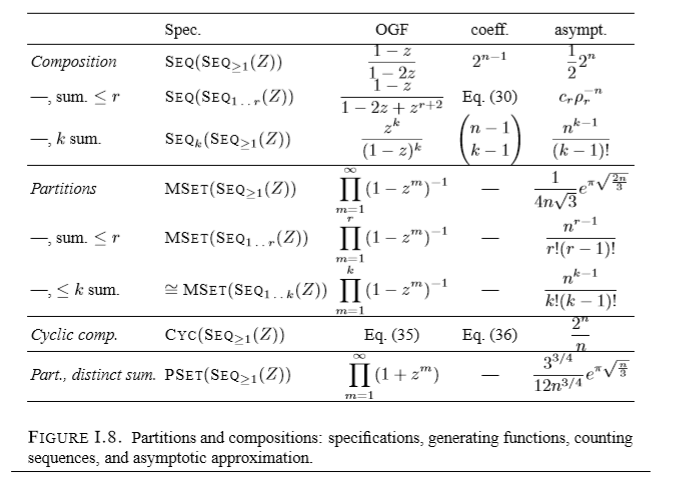
提醒一下，那个无限制的Composition个数是\(2^{n-1}\)，智力题，想象\(n-1\)个隔板。拿mma求解可以用Combinatorica程序包里的Compositions函数
提醒一下，那个n的k部分Partition个数是\([z^n]z^k \prod\limits_{m=1}^{k}(1-z^m)^{-1}\)。mma代码就是IntegerPartitions[2010, {3}];Length@%
提醒一下，如果记\(p(n,k)\)是n的k部分的partition的方案个数，那么有\(p(n,k)=p(n-1,k-1)+p(n-k,k)\).证明是考虑最小的那个和数，如果是1对应于\(p(n-1,k-1)\)这一项，如果>1对应于\(p(n-k,k)\)这一项.更详细的解释看这个帖子。

最后还有一些

I.14写成显式公式就是

\[\sum_{j}(-1)^{j}\left(\begin{array}{l} k \\ j \end{array}\right)\left(\begin{array}{c} n-r j-1 \\ k-1 \end{array}\right) \]

I.15用q-analogue很容易理解，可以看我写过的这篇文章

SEE ALSO

Restricted Weighted Integer Compositions and Extended Binomial Coefficients
Compositions of n with parts in a set

书主要涉及到的是Analytic Combinatorics

资料来自网络

Basic Hypergeometric Series这本书的8.10节也给出了一些公式

Let \(p(n)\) be the number of integer partitions of \(n\).

\[\begin{aligned} (q;q)_{\infty}^{-1} &=\prod\limits_{k=0}^{\infty} (1-q^{k+1})^{-1} \\ &= \sum\limits_{k_1\geq 0} \sum\limits_{k_2\geq 0} \cdots q^{k_1 \cdot 1 + k_2 \cdot 2+\cdots} \\ &= \sum\limits_{n=0}^{\infty} p(n) q^n \end{aligned} \]

Hardy和Ramanujan在1918年给出\(p(n)\)在\(n\to \infty\)的渐近分析

\[p(n) \sim \frac{1}{4n\sqrt{3}} \big[ \pi (\frac{2n}{3})^{ \frac{1}{2} } \big] \]

(i)

\(p_N(n)\), the number of partitions of \(n\) into parts \(\leq N\), which is given by the g.f.

\[(q;q)_N^{-1} =\sum\limits_{n=0}^{\infty} p_N(n) q^n \]

(ii)

\(p_e(n)\), the number of partitions of an even integer \(n\) into even parts, generated by

\[\begin{aligned} (q^2; q^2)_{\infty}^{-1} &=\prod\limits_{k=0}^{\infty} (1-q^{2k+2})^{-1} \\ &= \sum\limits_{n=0}^{\infty} p_e(n) q^n \end{aligned} \]

(iii)

\(p_{\text{dist}}(n)\), the number of partitions of \(n\) into distinct positive integers, generated by

\[\begin{aligned} (-q;q)_{\infty} &=\sum \limits_{k_1=0}^{1} \sum\limits_{k_2=0}^{1} \cdots q^{k_1\cdot 1 +k_2 \cdot 2+\cdots} \\ &= \sum\limits_{n=0}^{\infty} p_{\text{dist}} (n) q^n \end{aligned} \]

where \(n=k_1\cdot 1 +k_2\cdot 2+\cdots +k_n \cdot n, \quad 0\leq k_i\leq 1,1\leq i\leq n\)

(iv)

\(p_0(n)\), the number of partitions of \(n\) into odd parts, generated by

\[\begin{aligned} (q; q^2)_{\infty}^{-1} &=\prod\limits_{k=0}^{\infty} (1-q^{2k+1})^{-1} \\ &= \sum\limits_{n=0}^{\infty} p_0(n) q^n \end{aligned} \]

分拆方案数里的一些等式

没记错的话是可以找到bijection的，可以看我的这个帖子。

Euler's partition identity

the bijection between case 1 and case 2.

1. distinct parts
2. all elements are odd

\[p_{\text{dist}}(n) = p_0(n) \]

---

the bijection between these 2 cases:

1. Integer partition of \(n\), all parts differ by \(\geq 2\), i.e. The so-called super-strict integer partition
2. Integer partition of \(n\), \(\text{ distinct parts }\), \(\text{each even part}\) \(>2\cdot (\# \text{odd parts})\).

---