【读书笔记】组合计数中的行列式方法 专题2 欧拉回路,the BEST theorem
目录
专题2-欧拉回路,the BEST theorem
一些定义
- An Eulerian path is a path in the graph that visits every edge exactly once.
- If the path starts and ends at the same vertex,then it is called an Eulerian cycle.
- We say \(G\) is an Eulerian graph if it has an Eulerian cycle.
一个有向图是欧拉的充要条件
Theorem 1.4.8 A directed graph is Eulerian if and only if it is connected and every vertex \(v\) satisfies \(indeg(v) = outdeg(v)\).
定理1.4.8 一个有向图而言,它是欧拉的当且仅当对所有节点出度等于入度。
BEST定理

BSET定理推论
在欧拉有向图中,每个节点的有向生成树数目都是相等的。

k-ary de Bruijn sequence定义
A k-ary de Bruijn sequence of order n
定义为一个cyclic word,长度是\(k^n\),用的字母表是{0,1,...,k-1},
它的每一个subword正好遍历【长度为\(n\),用字母表为{0,1,...,k-1}组成的\(k^n\)个序列】(每个出现一次)
举个例子,我从维基百科截的图:
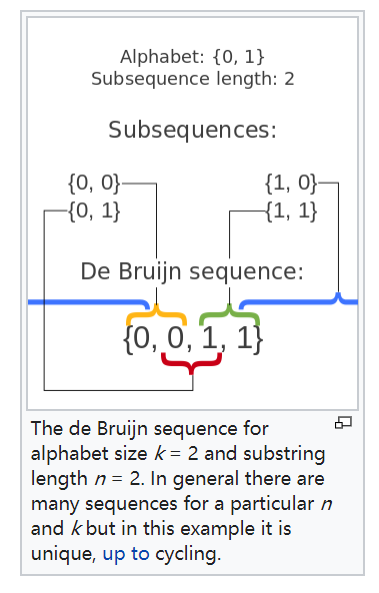
BSET theorem在k-ary de Bruijn sequences of order n计数 中的应用
建图呗。下面这也是维基截的图。
比如你想求解2-ary de Bruijn sequences of order 3的数目,每个节点的序列长度是3,
数哈密顿路径。(收集的序列就是点构成的序列)
或者,你想求解2-ary de Bruijn sequences of order 4的数目,每个节点的序列长度是3,
数欧拉环。 (收集的序列就是【边,形如e_1,e_2,e_3...】构成的序列)
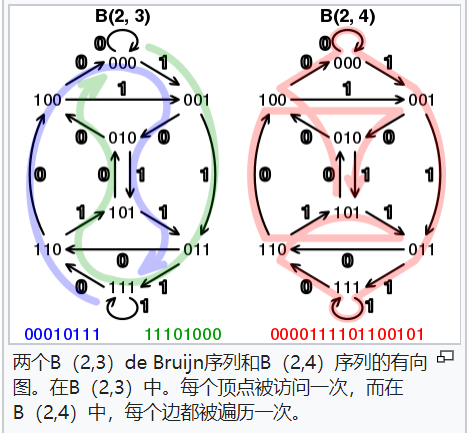
下面定理证明中用到的是把长度为n-1的序列作为点,找到欧拉环。




