欢迎访问yhm138的博客园博客， 你可以通过 [RSS] 的方式持续关注博客更新

MyAvatar

yhm138

HelloWorld！

【读书笔记】组合计数中的行列式方法

看不懂啦停止更新啦
由于过长分成了若干部分。下面的四个专题链接导向我的博客园随笔

专题1-生成树

专题2-欧拉回路，the BEST theorem

专题3-Perfect matchings: the Pfaffian method

专题4-Routings: the Lindstrm–Gessel–Viennot lemma

upd 2020-07-22 最后一部分加上去了，越写越烂，，，，
upd 2020-07-21 23:00 增加了Routings: the Lindstrm–Gessel–Viennot lemma章节，写到了这一节的Example3
upd 2020-07-14 17:36 增加了完美匹配的部分，已经快看不懂了😭
upd 2020-07-14 增加了欧拉路径和BEST theorem 章节
做笔记，不然学了忘
流水账警告❗

目录

把计数问题转化为计算矩阵行列式

预备知识

adjacency matrix 中文是邻接矩阵

有向图 The adjacency matrix \(A = A(G)\) is the\(V×V\) matrix whose entries are

\(a_{uv}\)= number of edges from u to v.

无向图 The (undirected) adjacency matrix \(A = A(G)\) is the \(V ×V\) matrix whose entries are

\(a_{uv}\) = number of edges connecting u and v.

一些结论

image-20200701093635006

不解释，邻接矩阵定义和矩阵乘法定义

算矩阵幂\(A^n\) ，如果\(A\)可对角化是容易计算的

嗯其实也有办法，我找到了《矩阵分析与应用》(第2版)7.3.3矩阵幂的计算，我放在末尾附录了

image-20200701093728920

第一个等号是等比数列的求和，第二个等号是克拉姆法则

image-20200701094754328

不解释

\(x\)我楞了一下，应该是\(1×1\)的

\(det(A-xI)=(x-\lambda_1)...(x-\lambda_k)\)

证明那里\(Q(x)=(1-\lambda_1x)...(1-\lambda_kx)\)我楞了一下，你把A对角形式带进去就比较容易理解了

image-20200701100239247

\(u,v\)和\(i,j\)记号混用，意思是那么个意思

联系了前面的Corollary 1.4.2

应用

Example1 项链染色

\(n\)个珠子围成一圈，给你\(k\)种颜色来染色,要求相邻颜色不同，求方案数目\(f(n,k)\)。(旋转和翻转视为不同的方案)

把\(k\)种颜色想成\(k\)个节点，完全图\(K_k\) ，邻接矩阵是\(A=J-I\) ，\(J\)是全1矩阵

\(A\)的\(k\)个特征值是\(-1,--1,...,-1,k-1\)

答案就是此图中长度为\(n\)的closed walk的数目

利用前面的Corollary 1.4.3

答案是\((k-1)^n+(k-1)(-1)^n\)

Example2 Words with forbidden subwords,1

给定一长\(n\)的字符串，只由{a,b}组成，且不会有子串aa(子串是连续的)。问你方案数目\(f_n\)。

说实话这个递推方程都能直接写，\(f_n=f_{n-1}+f_{n-2},f_{1}=2,f_{2}=3\)

建图就是节点a和节点b，边a→b,b→a,b→b

\[A=\begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \]

\[A^n=\begin{pmatrix} Fibonacci[n-1] & Fibonacci[n] \\ Fibonacci[n] & Fibonacci[n+1] \end{pmatrix} \]

\(f_n\)是\(A^{n-1}\)的元素和，是Fibonacci[n+2]

Example3 Words with forbidden subwords,2

给定一长\(n\)的cyclic word，只由{a,b}组成，且不会有子串aa，abba(子串是连续的)。问你方案数目\(g_n\)。

不会，吃了没文化的亏，看不懂cyclic word是啥

我认为是好比babbb，然后它就是你的重复单元

。。。babbb|babbb|babbb|babbb。。。里找子串

这样就解释通了

image-20200701172753574

Example4 Monomer-dimer problem

给你1×1和1×2的砖都是无数个，问你无重叠填充\(m×n\)大矩形的方案数目

这里介绍简单的情形，\(m=3,n=5\)

强制加上顺序，一列一列的铺，共有6条竖线

每次从上往下数，突出计0，不突出计1

一种方案的图解如下，

image-20200701161005855

111--110-->011-->101-->010-->111.​

这正好对应图\(G\)从111到111的长为\(5\)路径

要求的答案就是111到111的长度为6的路径数

图\(G\)到底长什么样呢？规律不是很明显

比如：

000到000肯定是0条边，

111到111有3种铺法（2+1，1+2，1+1+1），111到111有3条边

101到111有1条

110到111有2条(1+1,2)

图G长这样

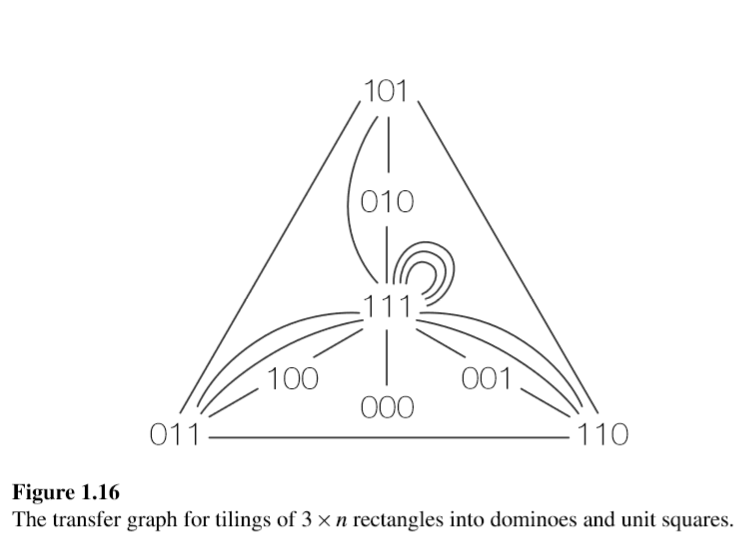
image-20200701162001669

接着图的邻接矩阵写出来就可以上手算啦

专题1-生成树

这里研究的第一个问题就是图的生成树计数问题 (节点带序，1-2-3和1-3-2不同)

记号说明

image-20200701152011254

A principal cofactor \(L_v(G)\) is obtained from \(L(G)\) by removing the \(v\)th row and \(v\)th column for some vertex v.

基尔霍夫矩阵树定理

image-20200701152034531

证明我看不懂

矩阵树定理的应用-一些典型图的生成树数目

image-20200701105531143

给一个完全图的生成树数目的证明:

image-20200701155040606

塔特有向矩阵树定理

image-20200701152141744

有向矩阵树定理证明

image-20200701152217878

专题2-欧拉回路，the BEST theorem

一些定义

  1. An Eulerian path is a path in the graph that visits every edge exactly once.
  2. If the path starts and ends at the same vertex,then it is called an Eulerian cycle.
  3. We say \(G\) is an Eulerian graph if it has an Eulerian cycle.

一个有向图是欧拉的充要条件

Theorem 1.4.8 A directed graph is Eulerian if and only if it is connected and every vertex \(v\) satisfies \(indeg(v) = outdeg(v)\).

定理1.4.8 一个有向图而言，它是欧拉的当且仅当对所有节点出度等于入度。

BEST定理

image-20200714082222785

BSET定理推论

在欧拉有向图中，每个节点的有向生成树数目都是相等的。

image-20200714082812360

k-ary de Bruijn sequence定义

A k-ary de Bruijn sequence of order n

定义为一个cyclic word，长度是\(k^n\),用的字母表是{0,1,...,k-1},

它的每一个subword正好遍历【长度为\(n\),用字母表为{0,1,...,k-1}组成的\(k^n\)个序列】(每个出现一次)

举个例子，我从维基百科截的图：

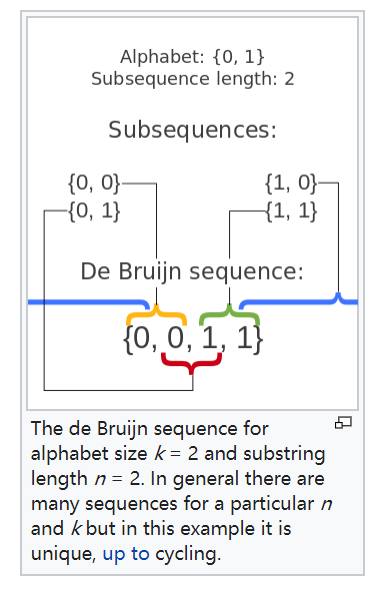
image-20200714084151778

BSET theorem在k-ary de Bruijn sequences of order n计数 中的应用

建图呗。下面这也是维基截的图。

比如你想求解2-ary de Bruijn sequences of order 3的数目，每个节点的序列长度是3，

数哈密顿路径。（收集的序列就是点上的序列）

或者，你想求解2-ary de Bruijn sequences of order 4的数目，每个节点的序列长度是3，

数欧拉环。 （收集的序列就是【边和边的发出点】构成的序列）

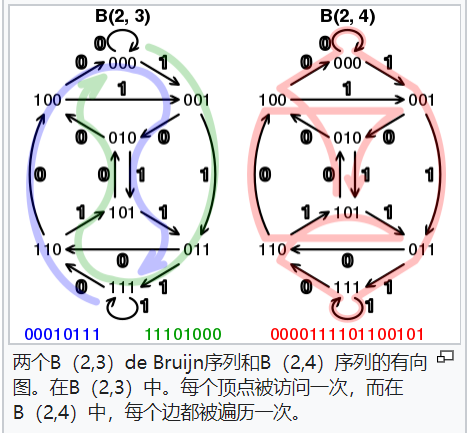
image-20200714085752383

下面定理证明中用到的是把长度为n-1的序列作为点，找到欧拉环。

image-20200714085031891

彩蛋-超排列

“我对普通的人类没有兴趣，你们只要能求出超排列的准确公式，就尽管来找我吧！以上”

Wikipedia Superpermutation

专题3-Perfect matchings: the Pfaffian method

一些定义

  1. 一个图\(G\)的完美匹配\(M\)是说一系列边，使得\(G\)的每一个点都在且仅在\(M\)的一条边上。或者你从字面理解：\(2m\)个点正好分成\(m\)组，每组2个，...

  2. skew-symmetric matrix \(A^T=-A\) (就是说关于主对角线对称的元素是相反数，\(a_{ij}=-a_{ji}\))

  3. Pfaffian的定义。emm这里书讲得不清楚，直接截图维基。

    Pfaffian是对满足\(A^T=-A\)的矩阵\(A\)定义的。

    image-20200714170239923

  4. 定理 \(det(A)=\operatorname{Pfaffian}(A)^2\) 证明看不懂

  5. 有向图的邻接矩阵 当然有\([S(G)]^{T}=-S(G)\) \(s_{i j}= \begin{cases}1 & \text { if } i \rightarrow j \text { is an edge of } G \\ -1 & \text { if } j \rightarrow i \text { is an edge of } G \\ 0 & \text { otherwise. }\end{cases}\)

用2×1的砖密铺a×b的大矩形的方法数

假设了\(b\)是偶数是因为：都是奇数肯定密铺不了

image-20200714171252369

这里不写了 ┏(゜ロ゜;)┛

专题4-Routings: the Lindstrm–Gessel–Viennot lemma

一些定义

  • DAG 有向无环图
  • \(\mathrm{wt}(e)\) 边的权重
  • \(\mathrm{wt}(P)=\prod \mathrm {wt}(e)\) 路径的权重
  • \(\mathrm{wt}(R)=\prod _{i=1}^n \mathrm {wt}(P)\) routing的权重
  • 源，汇 Let S ={s1,...,sn} and T ={t1,...,tn} be two (not necessarily disjoint) sets of vertices,which we call sources and sinks,respectively
  • Routing定义 A routing from S to T is a set of paths P1,..., Pn from the n sources s1,...,sn to the n sinks t1,...,tn such that no two paths share a vertex.
  • Let π be the permutation of [n] such that \(P_i\) starts at source \(s_i\) and ends at sink \(t_{π(i)}\), and define sign(R) = sign(π).
  • path matrix Q定义 \(q_{ij}=\sum\limits_{P\ path from\ s_i to\ t_j }\mathrm{wt}(P)\) 考虑Q的元素时只是看\(s_i\)到\(t_j\)的所有路径

原文如下

image-20200716102605027

the Lindstrm–Gessel–Viennot lemma

维基百科词条-Lindstrm–Gessel–Viennot lemma

式子右边的求和是对\(S\)到\(T\)的所有routings

【In particular】那里是说，

如果正好图还有这样的性质：每条边权都是1，而且\(S\)到\(T\)的所有routing都是1->1,2->2...这样的形式，那么\(\operatorname{det}\ Q=\text{number of routings from S to T}\)

image-20200716101859444

Lindstrm–Gessel–Viennot lemma 应用

Example1 Binomial determinants


\(\begin{gathered} \begin{pmatrix} a_1,...,a_n \\ b_1,...,b_n \end{pmatrix} \end{gathered}\)记号表示的是那个行列式

...开始我还看不懂为什么there are \(\begin{gathered} \begin{pmatrix} a_i \\ b_j \end{pmatrix} \end{gathered}\) SE paths from \(A_i\) to \(B_j\)

SE path 是说south 和 east ，我以为是往东往北了

since every SE routing from A to B takes Ai to Bi for all i, 这是因为0≤a1 <···<an and 0≤b1 <···<bn ; points A ={A1,...,An} and B ={B1,...,Bn} where Ai = (0,ai) and Bi = (bi,bi) for1≤i≤n 然后你还要要走SE path

Example2 Counting permutations by descent set

image-20200721085130010

先定义一个n排列的decent set是说一个集合\(S\)，集合\(S\)的元素是index i使得\(\pi_i>\pi_{i+1}\)

然后问你 number of permutations of [n] with descent set\(\{c_1,...,c_k\}\)

可以构造一个A到B的SE routings构成bijeciton，答案是\(\begin{gathered} \begin{pmatrix} c_1,...c_k,n \\ 0,c_1,...,c_k \end{pmatrix} \end{gathered}\)(前面的行列式记号)

Example3 Rhombus tilings and plane partitions

让你用【1,1,1,1 60° 120°】的菱形密铺边长为\(n\)的正六边形(需要按照网格线摆放)。问你方案数\(R_n\)

image-20200721225736163

有几种观点：

  1. 看成正视图，如此，容易看到3种【\(60^°120^°\)的菱形】每种都是\(n^2\)个

  2. 思路是把每个菱形都看成是两个正三角形拼接，每个正三角形的中心作为一个节点，一般而言(内部的)每个节点和最近的3个节点相连。构成hexagonal grid。
    相邻两个节点相连如果两个等边三角形上面正好是覆盖所用的菱形。问题转变为求完美匹配。

  3. plane partition理解。从观点1的角度往前一步，给出【表明每个格子上垒有多少个cube】的俯视图。 an array of nonnegative integers(finitely many of which are non-zero)that is weakly decreasing in each row and column. We conclude that \(R_n\) is also the number of plane partitions whose non-zero entries are at most n, and fit inside an n×n square.

  4. 从观点1的角度出发，看高度\(n-0.5\)，...，高度2.5，高度1.5，高度0.5，截cube stack的曲线。这对应于 n sources S1,...,Sn on the left to the sinks T1,...,Tn ，（S1到T1,S2到T2....）的routing。利用前面的Lindstrm–Gessel–Viennot lemma，矩阵元素\(\begin{gathered} \begin{pmatrix} 2n \\ n+i-j \end{pmatrix} \end{gathered}\)

    \[R_n=det\bigg[\begin{gathered} \begin{pmatrix} 2n \\ n+i-j \end{pmatrix}\bigg] \end{gathered}_{1\leq i,j\leq n}=\prod\limits_{i,j,k=1}^{n}\frac{i+j+k-1}{i+j+k-2} \]

Example4 Catalan determinants, multitriangulations, and Pfaffian rings

定义一个序列\(A=(a_0,a_1,a_2,...)\)的Hankel矩阵\(H_n(A)\)和\(H_n'(A)\)

\[\begin{equation} H_n(A) =\begin{pmatrix} a_0 & a_1 & \cdots\ &a_n\\ a_1 & a_2 & \cdots\ & a_{n+1}\\ \vdots & \vdots & \ddots & \vdots \\ a_n & a_{n+1} & \cdots\ & a_{2n}\\ \end{pmatrix} \end{equation} \]

和

\[\begin{equation} H_n'(A) =\begin{pmatrix} a_1 & a_2 & \cdots\ &a_{n+1}\\ a_2 & a_3 & \cdots\ & a_{n+2}\\ \vdots & \vdots & \ddots & \vdots \\ a_{n+1}& a_{n+2} & \cdots\ & a_{2n+1}\\ \end{pmatrix} \end{equation} \]

如果我们知道 the Hankel determinants \(det \ H_n(A)\) and \(det\ H_n'(A)\) ，而且对所有的n它们都是非零的，我们可以利用递推关系从 \(a_0,…, a_{k-1}\)来恢复每一个 \(a_k\) 。

如果序列是卡特兰序列\(C=(C_0,C_1,C_2,...)\)的话，恰好有一种很好的解释。

image-20200722072742092

式(1.9)是许多事物的组合计数。

the number of k-fans of Dyck paths of length \(2(n−2k)\)

image-20200722083917992

式（1.9）也是the number of k-fans of Dyck paths of length \(2(n-2k)\)

the number of k triangulations of an n-gon

k-crossing 定义 a k-crossing in an n-gon to be a set of k diagonals that cross pairwise（两两相交）

k-triangulation定义 A k-triangulation is a maximal set of diagonals with no(k+1)-crossings.

式(1.9)也是 the number of k triangulations of an n-gon 。

Example5 Schr¨oder determinants and Aztec diamonds

image-20200722085218358

image-20200722085241832

image-20200722085253155

计算行列式

这里方法太多了哈，方法不要太多

Of course, when we wish to evaluate a new determinant, one first step is to check whether it is a special case of some known determinantal evaluation

确实确实，能找到现成的或者是现成的特例情形绝不自己动手

附录

利用Cayley-Hamilton定理变形一下，

先求特征值，再解\(n\)个线性方程构成的方程组

算法和例子如下，如果矩阵阶数\(n\)也很大的话就。。。。

image-20200701101908326

书用的是Handbook of enumerative combinatorics

资料来自网络

posted @ 2020-07-01 22:51  yhm138  阅读(790)  评论(0)  编辑  收藏  举报