Tutte多项式和图多项式
目录
Tutte Polynomial
你可能会在图的谱理论里看到Tutte Polynomial
https://en.wikipedia.org/wiki/Tutte_polynomial
定义式
\[T_{G}(x, y)=\sum_{A \subseteq E}(x-1)^{k(A)-k(E)}(y-1)^{k(A)+|A|-|V|}
\]
其中\(k(A)\)是图\((V,A)\)的联通分量数目
individual points (x,y)为不同值时给出不同的组合计数
(2,1) 给出森林数量,看起来这个会多一点
(1,1) 给出生成森林的数量
(1,2) 给出生成子图的数量
(2,0) 给出无环orientation的数量
(0,2) 给出强连接orientation的数量
(2,2) 给出\(2^{|E|}\)
tutte是各种图多项式的外延
y=0 就成为了色多项式 chromatic polynomial
x=0 就成为了流多项式 flow polynomial
x=1 就成为了可靠性多项式 reliability polynomial
啥是无环oritation
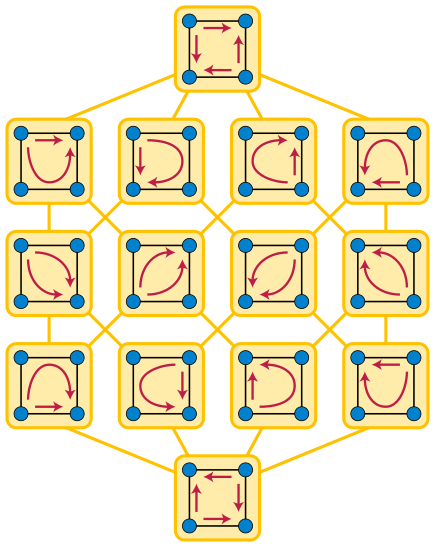
啥是强连通oritation
对一个无向图,每条边分配一个direction,最后使得得到的有向图是强连通的。
更多的图多项式

GraphData["HeawoodGraph", "CliquePolynomial"]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号