Mathemaitca做蒙特卡罗积分法
背景知识
蒙特卡罗积分法是一种利用模拟来近似计算定积分值\(\int_a^b f(x)dx\)的一种方法
公式是
\[\int f(x) \mathrm{d} x=\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)} \quad X_{i} \sim p(x)
\]
\({p\left(X_{i}\right)}\)是随机变量服从分布的PDF在\(X_{i}\)处的值
mma代码
这里以计算\(\int_0^\pi \sin(x)dx\)为例,这个定积分的精确值是2
步骤:
1.取1000000个iid且[0,Pi]均匀分布的r.v.,
2.分别计算\(\frac{f\left(X_{i}\right)}{p\left(X_{i}\right)}\),再对他们求平均值
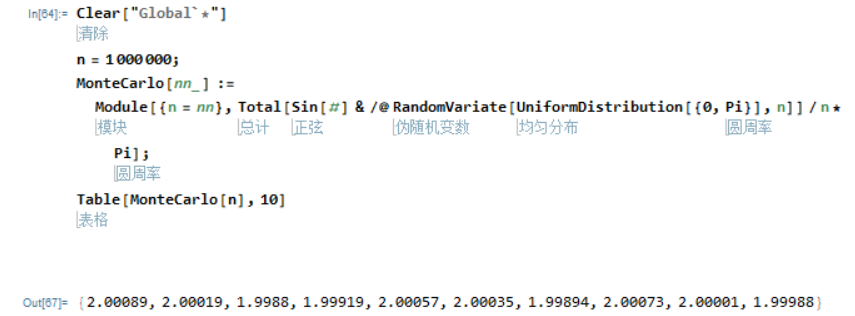
Clear["Global`*"]
n = 1000000;
MonteCarlo[nn_] :=
Module[{n = nn},
Total[Sin[#] & /@ RandomVariate[UniformDistribution[{0, Pi}], n]]/
n*Pi];
Table[MonteCarlo[n], 10]
结果如下
FYI
有几点注意事项
使用蒙特卡洛积分法求积分涉及到两个问题:1.如何对一个任意分布函数进行抽样; 2.如何减少方差。
首先是给定一个概率密度函数,如何对其进行采样,使采样满足其概率分布。其中有逆变换算法和取舍算法。更多的信息可以看这篇博客。
接着是如何减少方差。直观的理解,pdf()形状越接近f(),效果越好。更多的信息可以看这篇博客。
MCMC(Markov Chain Monte Carlo)。因为对于任意分布的概率函数的采样不容易做到,可以构造一个马尔可夫链(怎么构造?)之后在上面随机游走来取点。其中有Metropolis-Hasting 算法和Gibbs 采样法。更多的信息可以看这篇博客



