MATLAB,Mathematica研究三维空间中的旋转
放弃更新,都看这篇文档吧 https://krasjet.github.io/quaternion/quaternion.pdf 👍
https://www.zhihu.com/question/23005815/answer/483589712 quaternion.pdf文档作者本人krasjet的知乎回答
放弃更新,可以去看这篇文章 https://edu.uwa4d.com/lesson-detail/188/1051/0
你看这个repo也行 https://github.com/Krasjet/quaternion
三维空间旋转还是挺实用的,可能在游戏制作,3D模型,航海中用到
3维空间中的【绕过原点的轴旋转】的自由度是3,这是因为确定一个转轴的取向需要2个自由度(\(\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1\)),确定绕这个轴转动了多少角度需要1个自由度。我见过不同的描述方法,但是他们都可以用\(3\times3\)的旋转矩阵\(R\)描述。\(\vec{x}^{\prime}=R\vec{x}\)
一般来说你见到的R,行列式都是1。如果是-1的话说明还来了次镜像
RollPitchYawMatrix
在全局框架中的轴向旋转
推导矩阵\(R\)可以用mathematica来辅助进行
RollPitchYawMatrix[{\[Alpha], \[Beta], \[Gamma]}, {1, 2,
3}] /. {Cos[x_] :> Subscript[c, x],
Sin[x_] :> Subscript[s, x]} // MatrixForm

EulerMatrix
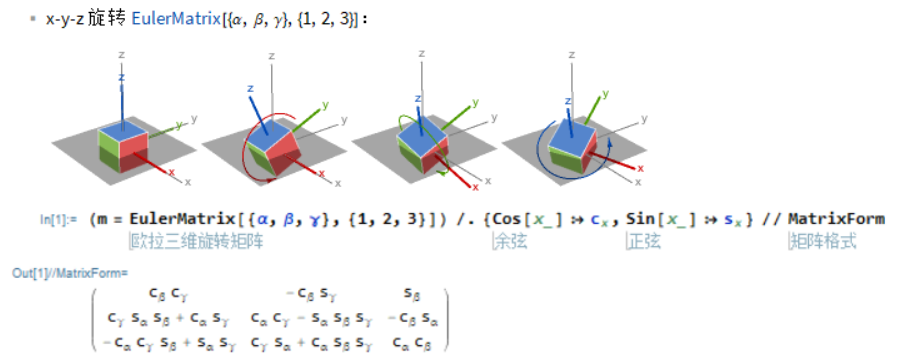
在内禀框架(理解为框架长在旋转物体上)的轴向旋转
推导矩阵\(R\)可以用mathematica来辅助进行
(m = EulerMatrix[{\[Alpha], \[Beta], \[Gamma]}, {1, 2, 3}]) /. {Cos[
x_] :> Subscript[c, x], Sin[x_] :> Subscript[s, x]} // MatrixForm
四元数形式
拿{a,b,c,d}来描述。把旋转对应到范数为1的四元数\(a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}\)。
满足\(a^{2}+b^{2}+c^{2}+d^{2}=1\),所以实际是3个自由度
上式写成向量形式就是
拿四元数来写就是这个公式:
其中,
\(
\mathbf{p}=\left(p_{x}, p_{y}, p_{z}\right)=p_{x} \mathbf{i}+p_{y} \mathbf{j}+p_{z} \mathbf{k}
\)
\(\mathbf{q}=e^{\frac{\theta}{2}\left(u_{x} \mathbf{i} + u_{y} \mathbf{j}+u_{z} \mathbf{k}\right)}=\cos \frac{\theta}{2}+\left(u_{x} \mathbf{i}+u_{y} \mathbf{j}+u_{z} \mathbf{k}\right) \sin \frac{\theta}{2}\)
\(\mathbf{p}^{\prime}=\left(p_{x}^{\prime}, p_{y}^{\prime}, p_{z}^{\prime}\right)\)
单次旋转
给出空间中一个点,将该点绕单位向量(k1 k2 k3)旋转一定角度theta,从而得到新点
变换矩阵\(\boldsymbol{R}=\boldsymbol{I}+\sin (\theta) \boldsymbol{K}+(1-\cos (\theta)) \boldsymbol{K}^{2}\)
其中\(\boldsymbol{K}=\left[\begin{array}{ccc} 0 & -k_{3} & k_{2} \\ k_{3} & 0 & -k_{1} \\ -k_{2} & k_{1} & 0 \end{array}\right]\)
它们间的变换关系
在内禀框架(理解为框架长在旋转物体上)的轴向旋转方案:三个转动角度
在全局框架中的轴向旋转的方案:三个转动角度
四元数的方案:存4个实数
单次旋转的方案:转轴方向单位向量(k1 k2 k3),转动角度theta
旋转矩阵的方案:存9个实数,存在冗余
一般你遇到的都是这5种之间转换来转换去
略(会出现死锁吗?)
也可以看这个 https://zhuanlan.zhihu.com/p/45404840
MATLAB编程练习(✅验证了没问题)
计算点\(p\)绕直线\(\frac{x-x_0}{k_x}=\frac{y-y_0}{k_y}=\frac{z-z_0}{k_z}\) (\(\color{red}{\vec{k}\text{是法向单位矢量}}\)) 按右手螺旋规则旋转\(\theta\)角得到的新点
main.m
clc;
clear all;
close all;
p=[2,0,0]; %旋转前的点
r0=[1,0,0]; %直线上的一点r0
x0=r0(1);
y0=r0(2);
z0=r0(3);
param=[0,1,0,pi/3];%分别是kx,ky,kz,theta
p_relative=p-r0; %旋转前的点相对r0的矢量
p_rotated=Rotation(p_relative,param)+r0 %p_rotated就是结果
Rotation.m
function p1=Rotation(p,param)
[row,col]=size(param);
if row==1&col==4
;
else
warndlg('请检查Rotation函数的第二个参数param的size是否是1*4');
end
if norm(param(1,end-1))-1.0<1e-8
;
else
warndlg('请检查Rotation函数的第二个参数param的kx,ky,kz构成的向量是否模长1')
end
[row,col]=size(p);
if row==1&col==3
;
else
warndlg('请检查Rotation函数的第一个参数p的size是否是1*3');
end
kx=param(1);
ky=param(2);
kz=param(3);
theta=param(4);
K=[0 -kz ky;
kz 0 -kx;
-ky kx 0];
R = eye(3) + sin(theta)*K + (1- cos(theta))*K*K; %罗德里格斯公式
p1= R*p'; %利用罗德里格斯公式计算的旋转后的点
p1=p1';
end
把上面的代码用Mathematica重写一遍(✅验证了没问题)
ClearAll["Global`*"];
On[Assert];
(*Define the point to be rotated,the line point,and rotation parameters*)
p = {2, 0, 0};(*Point before rotation*)
r0 = {1, 0, 0}(*Point on the line*)
param = {0, 1, 0, Pi/3};(*Rotation parameters:{kx,ky,kz,theta}*)
(*Define the Rotation function using Rodrigues' rotation formula*)
Rotation[p_, param_] :=
Module[{kx, ky, kz, theta, K, R, p1}, {kx, ky, kz, theta} = param;
Assert[kx^2 + ky^2 + kz^2 == 1];
K = {{0, -kz, ky}, {kz, 0, -kx}, {-ky, kx, 0}};
R = IdentityMatrix[3] +
Sin[theta]*K + (1 - Cos[theta])*MatrixPower[K, 2];
p1 = R . p;
p1]
(*Calculate the rotated point*)
pRelative = p - r0;
pRotated = Rotation[pRelative, param] + r0;
(*Display the result*)
pRotated
参考
https://en.wikipedia.org/wiki/Euler–Rodrigues_formula


 浙公网安备 33010602011771号
浙公网安备 33010602011771号