Mathemtica画出一个s域传递函数描述的系统的频域特性；z域传递函数描述的系统的频域特性
拿到的问题是这样的
拿双线性变换法做
双线性变换法：优点是克服多值映射关系、不会产生混叠失真；缺点是模拟到数字( s到z)的变换是非线性的，在高频处会有较大的失真。
研究拿到的s域函数的频域特性
2/((s + 1) (s + 3)) /. {s -> I*\[CapitalOmega] }
Plot[Abs[%], {\[CapitalOmega], -1000, 1000}]
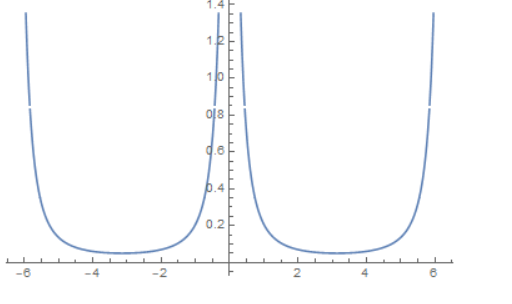
画出\(\frac{2}{(s+1)(s+3)}\)的频域特性
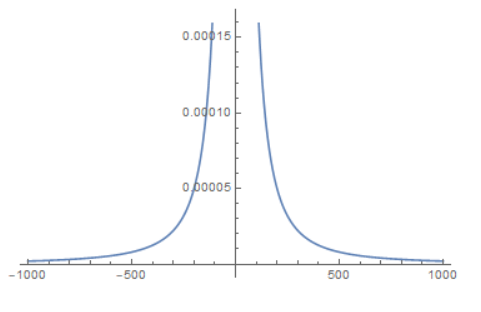
用那种最传统的双线性变换法得到一个z域函数
(*使用双线性变换法*)
T = 0.1;(*采样周期设置为0.1*)
2/((s + 1) (s + 3)) /. {s ->
2/T*(1 - z^{-1})/(1 + z^{-1})} // FullSimplify
% /. {z -> Exp[I*\[Omega]]}
Plot[Abs[%], {\[Omega], -2 Pi, 2 Pi}]
得到的z域传函是\(\frac{0.00414079 (z+1.)^2}{z (1. z-1.64389)+0.668737}\)
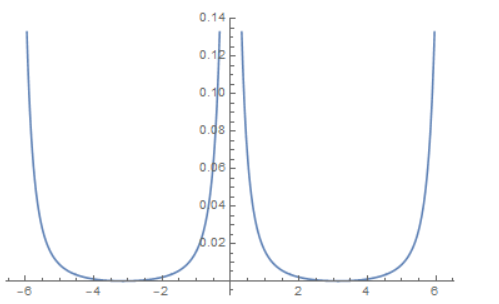
画对比图
Plot[{Abs[2/((1 + I*10 \[Omega]) (3 + I*10 \[Omega]))],
Abs[(0.004140786749482401` (1.` + E^(I \[Omega]))^2)/(
0.6687370600414079` +
E^(I \[Omega]) (-1.6438923395445135` +
1.` E^(I \[Omega])))]}, {\[Omega], 0, Pi},
PlotLegends -> Automatic]
画对比图的时候利用了数字角频率和模拟角频率间的互换关系
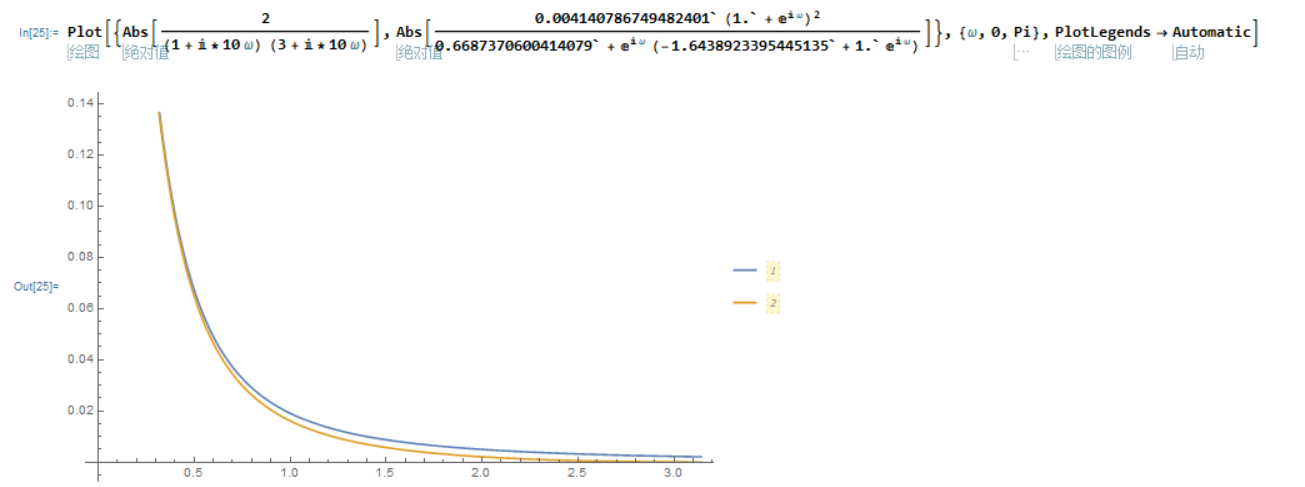
用脉冲响应不变法做一下
脉冲响应不变法：优点是模拟到数字的转换是线性转换，并且以数字滤波器的单位脉冲响应近似模拟滤波器的单位脉冲响应，因此有较好的时域逼近特性；缺点是：有频谱周期延拓效应，因此只能用于带限的频响特性，如衰减特性很好的低通或带通。
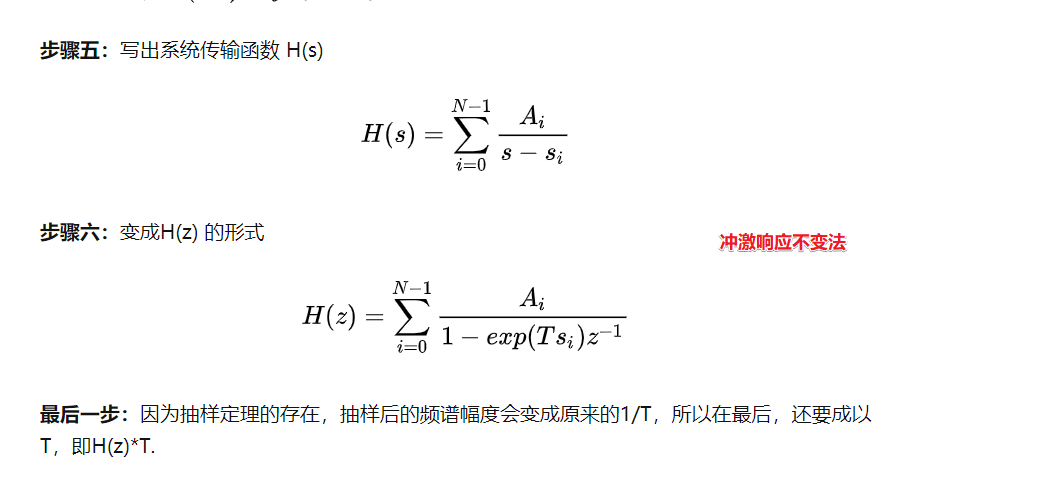
用那种最传统的脉冲响应不变法得到一个z域函数
T = 0.1;
InverseLaplaceTransform[2/((s + 1)*(s + 3)), s, t]
% /. {t -> n*T}
ZTransform[%, n, z] // FullSimplify
% /. {z -> Exp[I*\[Omega]]}
Plot[Abs[%], {\[Omega], -2 Pi, 2 Pi}]
得到的z域函数是\(z \left(\frac{1}{0.740818\, -1. z}+\frac{1}{z-0.904837}\right)\)
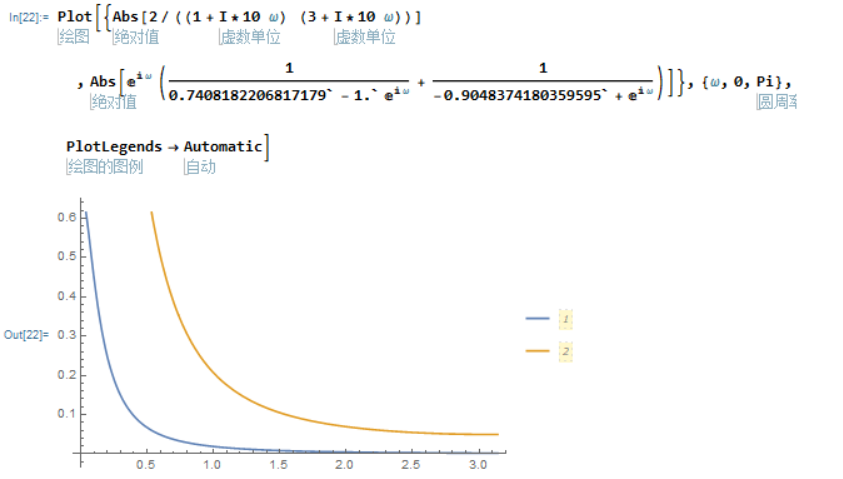
画对比图
Plot[{Abs[2/((1 + I*10 \[Omega]) (3 + I*10 \[Omega]))]
, Abs[E^(
I \[Omega]) (1/(0.7408182206817179` - 1.` E^(I \[Omega])) +
1/(-0.9048374180359595` + E^(I \[Omega])))]}, {\[Omega], 0, Pi},
PlotLegends -> Automatic]
