北京大学2020年强基计划数学试题 部分题目解答（Mathematica练习）
14，17没有做
试题地址
http://www.zizzs.com/c/202008/47535.html
1
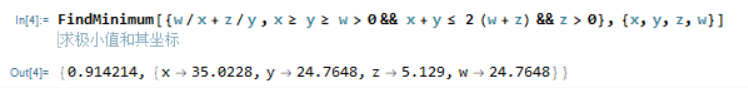
这里给的是取到最小值的时候的一组\(\mathrm{(x,y,z,w)}\)
2
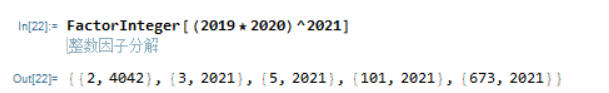
做到这答案就快出来了
转化问题为：
比如你选了\(2^{1}3^{2}5^{3}101^{4}673^{5}\),按照指数的奇偶性把这个映射成10101
考虑到这个问题答案是32：长度为5的0-1序列，共32种，你要从里面选出尽可能多的码片(允许每种多个)，使得其中任意两个码片的按位异或后不是全零序列，你最多可以选出2^5=32个
实际上这题答案也是32
3
用mma算的话，不止一种做法，我这里是其中一种做法
导出那个线性递推式还是有点技巧性在里面的
之后用矩阵幂来算(C++来写的话，建议写带模法的快速幂)
4
5
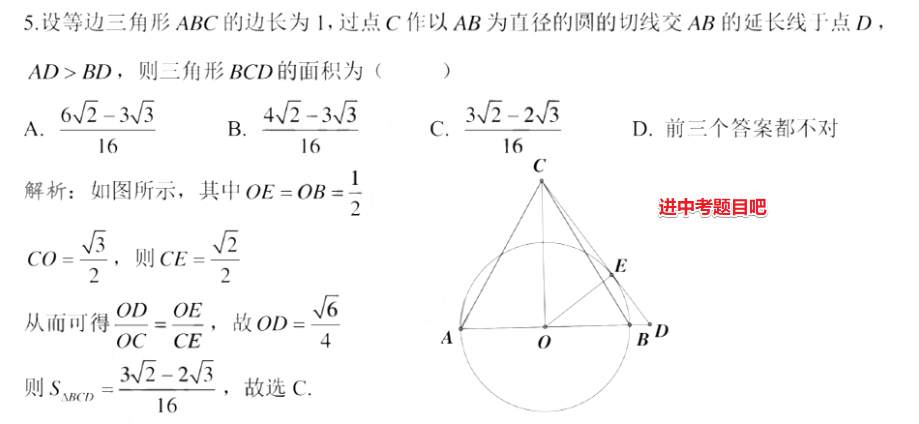
6
7
8
https://www.cnblogs.com/yhm138/articles/14580760.html
9
10
11
12
13
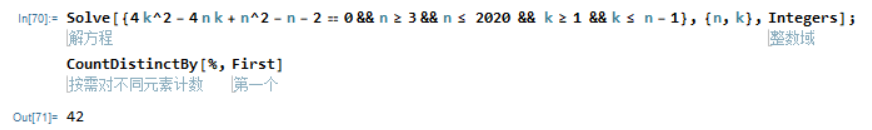
15
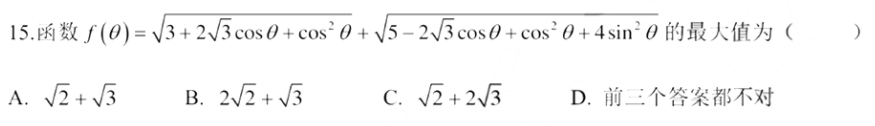
16
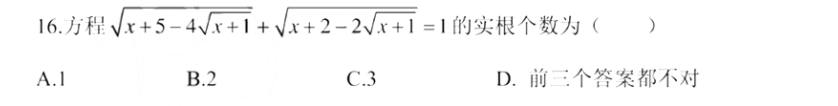
Reduce一下发现实际是一个闭区间，所以选择D
18
19
标答已经讲得很明白了
20
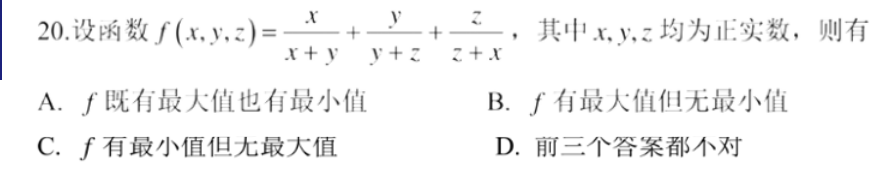
NMinimize[{x/(x + y) + y/(y + z) + z/(z + x), x > 0, y > 0,
z > 0}, {x, y, z}]
NMaximize[{x/(x + y) + y/(y + z) + z/(z + x), x > 0, y > 0,
z > 0}, {x, y, z}]
f没有最大值且没有最小值
