FIR和IIR——思维导图以及它们的基础知识

IIR滤波器的基本特征

①IIR滤波器的单位冲激响应长度无限。
②IIR滤波器很难保证线性相位，因为h（n）长度无限，很难保证其对称性。
③IIR滤波器当前时刻的输出不仅与当前及之前时刻的输入有关，还与之前时刻的输出关，也即是说IIR滤波器是递归的。
④IIR滤波器的优势源于其递归特性，如对同样的技术参数，IIR滤波器所需的系数更，效率更高。
⑤同样是由于其递归特性，IIR滤波器对有限字长比较敏感，容易出现稳定性的问题。⑥IIR滤波器不仅有零点，还有极点。为保证系统的稳定性，所有的极点都必须在单位圆，或者与零点恰好在单位圆上重合。通常情况对零点没有限制，但在某些特殊情况下，如最小相位滤波器中则要求零点也都在单位圆内。
⑦IIR滤波器常用零极图来进行分析。

FIR滤波器的基本特征

①FIR滤波器的单位冲激响应长度有限；
②由于长度有限，FIR滤波器总是稳定的；
③FIR滤波器当前时刻的输出仅与当前及之前时刻的输入有关；
④FIR滤波器一般是非递归的，因而对有限字长的影响不敏感；
⑤FIR滤波器的卷积运算可用FFT来实现；
⑥FIR滤波器为全零点系统。

线性相位FIR的话，看下面这张图片

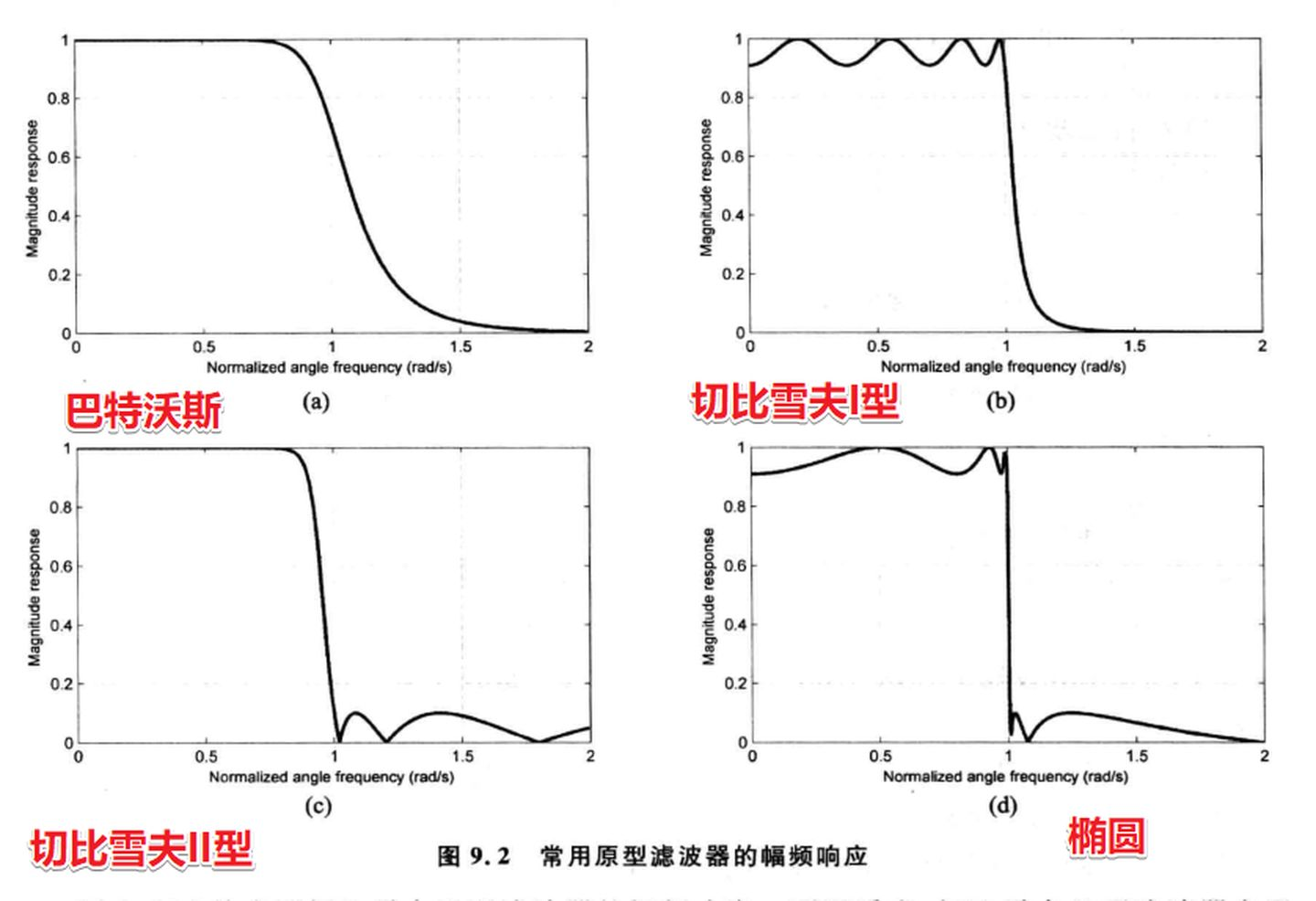
巴特沃斯滤波器幅频响应在整个通带和阻带都是单调递减的。另外，巴特沃斯滤波器没有零点，为全极点滤波器，并且极点均匀分布在s平面单位圆上。巴特沃斯滤波器具有通带内幅度响应最平坦的特性。

切比雪夫I型滤波器在通带中具有等波纹响应，在阻带单调变化。另外，切比雪夫I型滤波器是一个全极点滤波器，其极点位于s平面的椭圆上。

切比雪夫II型滤波器在通带单调变化，而在阻带具有等波纹响应。另外，切比雪夫II型滤波器既有零点也有极点，零点为纯虚数。正是由于切比雪夫II型滤波器存在零点，因而比切比雪夫I型滤波器有更好的群延时特性，即相位响应更线性。

椭圆滤波器在通带和阻带均表现为等波纹特性，它们的幅频响应和FIR等波纹滤波器类似。椭圆滤波器提供了最优的平方幅度响应，但在通带上的相位响应非线性较大。

本文内容全部来自《深入浅出数字信号处理》