SVM(支持向量机)初探
这几天接触了一些关于图像分类的论文,发现其中大多都用到了SVM,于是上网找了一些SVM的资料,得出一些理解。
维基百科上用这句话来描述SVM:
支持向量机将向量映射到一个更高维的空间里,在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面。分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大,分类器的总误差越小。
其实这句话不太完整:这是对于线性不可分的情况,而对于线性可分情况,就不用第一步“支持向量机将向量映射到一个更高维的空间里”了。
更完整的SVM简述:
支持向量机是一个二类分类器(至少最初是这样),它对于线性可分情况,在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面。分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大,分类器的总误差越小。而对于线性不可分情况,它将向量映射到一个更高维的空间,使其线性可分,然后做跟第一种情况同样的事情。
先解释一下三个红色字体的名词:
超平面:是 n 维欧氏空间中余维度等于一的线性子空间。对于二维空间,就把它想象成一条直线,对于三维空间就是一个平面。
线性可分、线性不可分:在样本向量所处的空间中,如果可以使用一个超平面将两类样本划分开,那么就叫做线性可分的。
最大间隔超平面:线性可分情况下,在使用超平面来分隔样本时,一般会有多个超平面满足条件,而最大间隔超平面就是满足条件的超平面中的一个,在它的超平面的两边建有两个互相平行的也满足条件的超平面。分隔超平面使两个平行超平面的距离最大化。
本文针对第一种(线性可分)情况。
搞清楚了上面的定义以后,我们的问题就是如何求得这个超平面,因为求得超平面的方程之后,即可得到分类器。
由上所述,给出样本:
我们可以设最大分隔超平面方程:
其中 是超平面上的点,
是超平面上的点,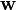 是垂直于超平面的向量。
是垂直于超平面的向量。
由于我们要求最大间隔,因此我们需要知道那两个互相平行的也满足条件的超平面。我们可以看到这些平行超平面可以由方程:
来表示。 由于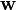 只是超平面的法向量,长度未定,是一个变量,所以等式右边的1和-1只是为计算方便而取的常量,其他常量只要互为相反数亦可。
只是超平面的法向量,长度未定,是一个变量,所以等式右边的1和-1只是为计算方便而取的常量,其他常量只要互为相反数亦可。
通过几何不难得到这两个超平面之间的距离是2/|w|,因此我们需要最小化 |w|。
我们需要保证对于所有的i满足条件:
然后这个问题就变成一个纯数学问题(二次规划),经过采用非负拉格朗日乘数 αi,得出结果:
其中只有很少的αi会大于0. 相应的
 就是支持向量,这些支持向量在边缘上并且满足
就是支持向量,这些支持向量在边缘上并且满足 ,所以
,所以。
求得w和b,即可求出最大分隔超平面方程,得到相应的二类线性分类器。



