LeetCode第24场周赛
Q1 逐步求和得到正数的最小值
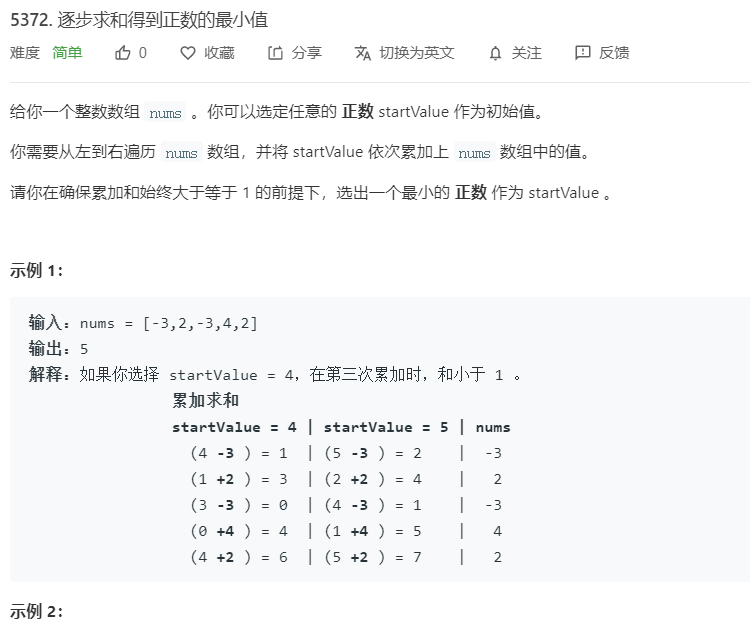
自己代码:AC 不精练
public int minStartValue(int[] nums) {
if(nums==null||nums.length==0) return 0;
int len=nums.length;
int res=0;
for(int i=1;i<Integer.MAX_VALUE;i++){
res=i;
int sum=i;
boolean flag=true;
for(int j=0;j<len;j++){
sum+=nums[j];
if(sum<1){
flag=false;
break;
}
}
if(flag){
return res;
}
}
return 0;
}
大佬:
解题思路:
-
当和大于等于0时,最小的正数应为1;
-
当和小于0时,最小的正数应为和取绝对值加一。
遍历所有累加和,得到所有应取最小正数中的最大值。
public int minStartValue(int[] nums) {
int ans = 1, sum = 0;
for (int num : nums) {
sum += num;
if (sum < 0) {
ans = Math.max(ans, -sum + 1);
}
}
return ans;
}
Q2 和为K的最少斐波那契数字数目

自己的代码:AC
思路:
1. 遍历过程中同时用集合保存符合要求的Fi数列,直到数列值大于k 终止遍历
2. 和为k,且要取得最少的数目 则每个加数越大越好,所有数列从后往前遍历
public int findMinFibonacciNumbers(int k) {
List<Integer> list=new ArrayList<>();
if(k==1) return 1;
if(k==2) return 1;
int one=1;
int two=1;
int temp=0;
list.add(1);
list.add(1);
while(temp<=k){
temp=one+two;
list.add(temp);
one=two;
two=temp;
}
//因为数列值最后要么等于k,要么大于k 需要为后续遍历确定起始点(逆序遍历)
int index=list.size()-1;
int count=0;
if(list.get(index)>k){
index-=1;
}
//开始遍历 设背包总容量为k
for(int i=index;i>=0;i--){
k-=list.get(i);
count++;
//超出剩余容量 恢复原先值
if(k<0){
k+=list.get(i);
count--;
continue;
}
//结束
if(k==0){
return count;
}
if(list.contains(k)){
count++;
return count;
}
}
return 0;
}
大佬:
解题思路:
- 注意k的最大值为10^9次方,则设置一个大小为45数组来存放1到45序列的斐波那契数
- 从后往前遍历
区别:
自己使用集合保存数列,其实可以根据k的最大值 来确定保存数列的数组的大小
public int findMinFibonacciNumbers(int k) {
int dp[] = new int[45];
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i<45;i++){
dp[i] = dp[i-1]+dp[i-2];
}
int s = 0;
for(int j = 44;j>=0;j--){
if(k >= dp[j]){
k = k-dp[j];
s++;
}
}
return s;
}

Q3 长度为n的开心字符串字典序第k小的字符串
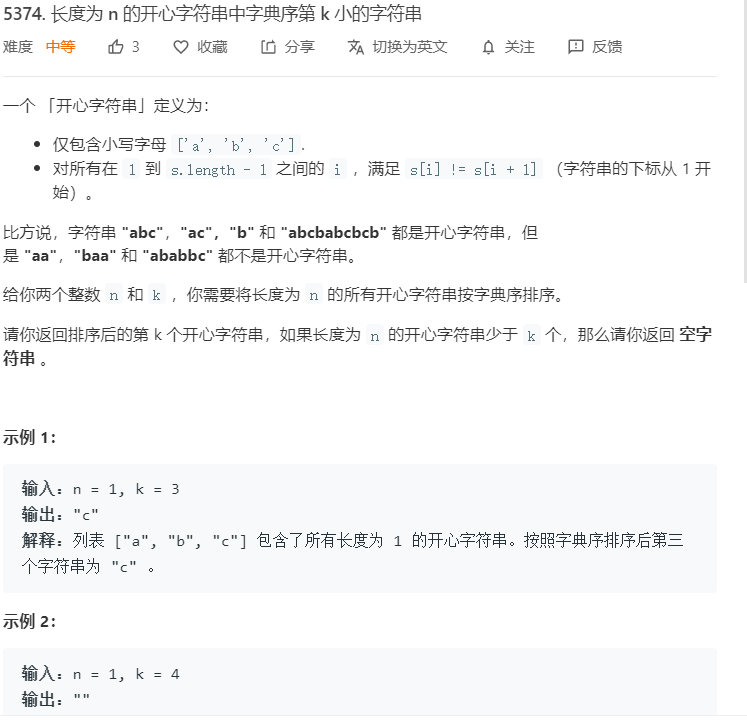
解题思路:
回溯 dfs
- 回溯过程中,每次添加一个字符(a, b, c),并使得添加的字符与前一个字符不同,当添加的字符数为n时,则找到长度为n的开心字符串。
- 对回溯过程得到对回溯过程得到的所有的开心字符串进行排序,返回第k个开心字符串
public String getHappyString(int n,int k){
List<String> res=new ArrayList<>();
backtracking("a", n-1, res);
backtracking("b", n-1, res);
backtracking("c", n-1, res);
if(res.size()<k){
return "";
}
Collections.sort(res);
return res.get(k-1);
}
public void backtracking(String s,int k,List<String> res){
if(k<0||(s.length()>1&&s.charAt(s.length()-1)==s.charAt(s.length()-2))){
return;
}
if(k==0){
res.add(s);
return;
}
backtracking(s+'a', k-1, res);
backtracking(s+'b', k-1, res);
backtracking(s+'c', k-1, res);
}
Q4 恢复数组
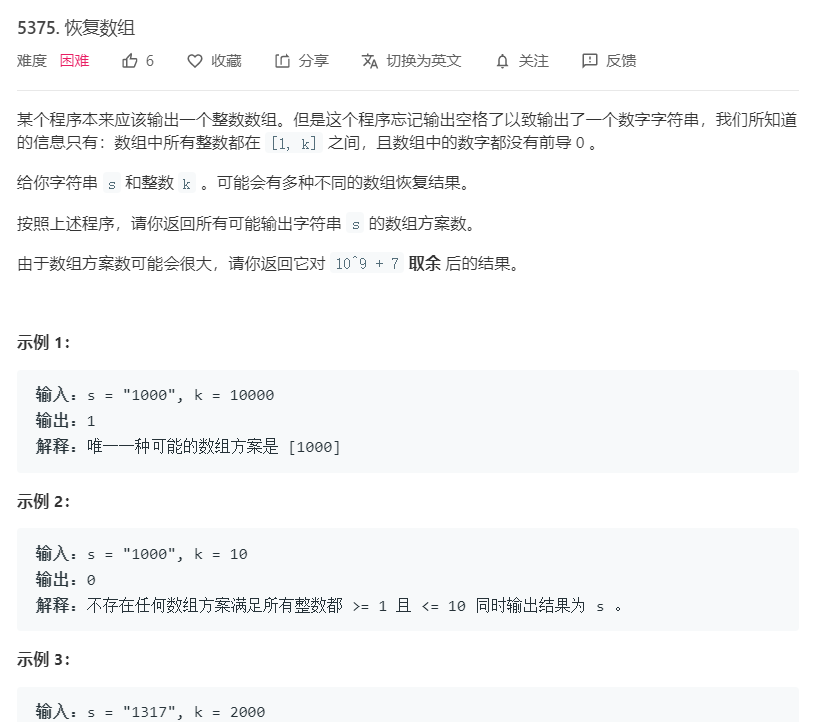
做不来。。。
思路:
动态规划

int m=1000000007;
public int numberOfArrays(String s, int k) {
long[] dp=new long[s.length()+1];
dp[s.length()]=1;
for(int i=s.length()-1;i>=0;i--){
//前导 零
if(s.charAt(i)=='0'){
dp[i]=0;
continue;
}
//解析分割出的第一个整数的值
long parseRes=0;
for(int j=i;j<s.length();j++){
parseRes=parseRes*10+s.charAt(j)-'0';
if(parseRes<=k)
dp[i]=(dp[i]+dp[j+1]) % m;
//当这个整数大于 k 时,就可以 break 了
else
break;
}
}
return (int)dp[0];
}


