CNN中的feature map

 

个人学习CNN的一些笔记，比较基础，整合了其他博客的内容

 

feature map的理解
　　在cnn的每个卷积层，数据都是以三维形式存在的。你可以把它看成许多个二维图片叠在一起（像豆腐皮竖直的贴成豆腐块一样），其中每一个称为一个feature map。

 

feature map 是怎么生成的？ 

• 输入层：在输入层，如果是灰度图片，那就只有一个feature map；如果是彩色图片（RGB），一般就是3个feature map（红绿蓝）

　　

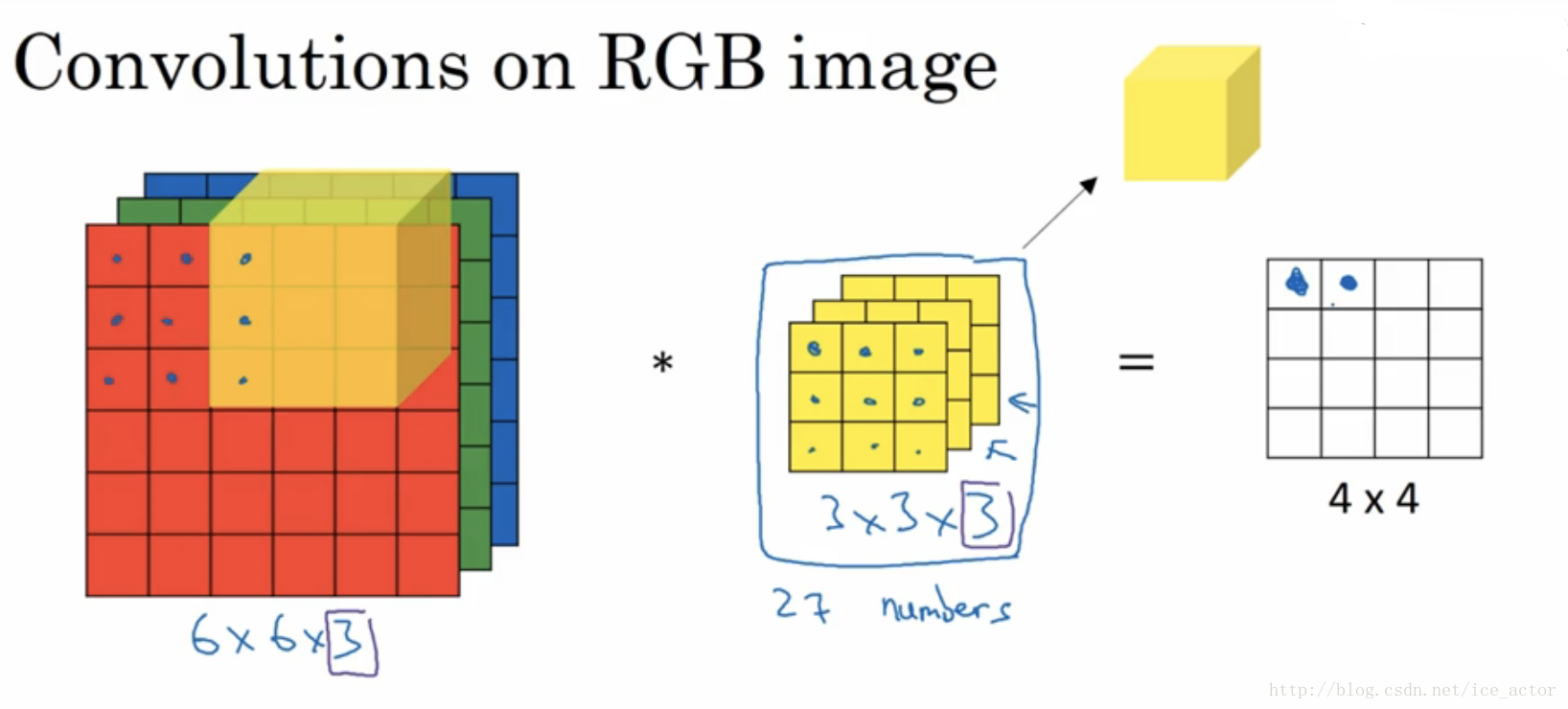
• 下图中三大部分依次是：输入RGB图片、卷积核（也称过滤器）、卷积结果（输出）。 * 代表卷积操作，最左部分三片代表3个feature map; 

如果是灰色图片（二维），则最左只有一片代表一个feature map，对应的卷积核（也是二维）

 

------------------------------------------------ 

 ------------------------------------------------ 

• 其它层：层与层之间会有若干个卷积核（kernel）（也称为过滤器）

 

(卷积核深度与初始图片的通道数一致）

上一层所有feature map 对应的 跟某个卷积核的所有层做卷积，结果相加（或者再加上偏置），都会产生下一层的一个feature map，有N个卷积核，下层就会产生N个feather map。

即：输入图片不论通道数是1（灰色）还是3（彩色）or其他值，经过卷积核处理后，都会统一拍平成深度为1的feature map。

有几个卷积核就生成几个feature map，与输入图片的通道数无关。

 

多个feature map的作用是什么？

在卷积神经网络中，我们希望用一个网络模拟视觉通路的特性，分层的概念是自底向上构造简单到复杂的神经元。楼主关心的是同一层，那就说说同一层。
　　我们希望构造一组基，这组基能够形成对于一个事物完备的描述，例如描述一个人时我们通过描述身高/体重/相貌等，在卷积网中也是如此。在同一层，我们希望得到对于一张图片多种角度的描述，具体来讲就是用多种不同的卷积核对图像进行卷，得到不同核（这里的核可以理解为描述）上的响应，作为图像的特征。他们的联系在于形成图像在同一层次不同基上的描述。

 

• 下层的核主要是一些简单的边缘检测器（也可以理解为生理学上的simple cell）。
• 上层的核主要是一些简单核的叠加（或者用其他词更贴切），可以理解为complex cell。

 

多少个Feature Map？

真的不好说，简单问题少，复杂问题多，但是自底向上一般是核的数量在逐渐变多（当然也有例外，如Alexnet），主要靠经验。

 

卷积核的理解

不懂的可以参考下面的博客

https://blog.csdn.net/cheneykl/article/details/79740810

 

卷积核（过滤器）个数的理解

我的前一篇博客中有写相关内容 https://www.cnblogs.com/yh-blog/p/10052543.html

• 第L-1层: 输入图形通道数 = 输入图像的层数 = 过滤器层数（三维坐标空间上是y方向）
• L层：输出图像通道数 = 过滤器个数 = 第L+1层输入图像层数...（不管输入和过滤层多少层，图像输入与每个过滤器卷积过后都是一层矩阵，影响输出层数的只有过滤器的个数）

 

如下图红线所示：

该层卷积核的个数，有多少个卷积核，经过卷积就会产生多少个feature map，也就是下图中 `豆腐皮儿`的层数、同时也是下图`豆腐块`的深度（宽度）！！

这个宽度可以手动指定，一般网络越深的地方这个值越大，因为随着网络的加深，feature map的长宽尺寸缩小，本卷积层的每个map提取的特征越具有代表性（精华部分），所以后一层卷积层需要增加feature map的数量，才能更充分的提取出前一层的特征，一般是成倍增加（不过具体论文会根据实验情况具体设置）！

 

 

参考博文：https://blog.csdn.net/csw19970124/article/details/83376842